Heim >Backend-Entwicklung >PHP-Tutorial >Eine Reihe von Diagrammen von Datenstrukturen, die Ihnen helfen, die Zeitkomplexität zu verstehen
Eine Reihe von Diagrammen von Datenstrukturen, die Ihnen helfen, die Zeitkomplexität zu verstehen
- little bottlenach vorne
- 2019-04-28 12:01:352312Durchsuche
Dieser Artikel verwendet eine Reihe von Bildern, um Ihnen das Verständnis der Zeitkomplexität zu erleichtern. Er ist interessant und anschaulich und hat einen gewissen Lernwert. Freunde, die interessiert sind, können vorbeikommen und es herausfinden .







Die Bedeutung der Zeitkomplexität
Was genau ist Zeitkomplexität? Stellen wir uns eine Szene vor: Eines Tages traten Xiao Hui und Da Huang gleichzeitig einer Firma bei...

Einen Tag später lieferten Xiao Hui und Da Huang jeweils ab In ihrem Warencode sind die vom Code an beiden Enden implementierten Funktionen ähnlich. Die einmalige Ausführung des Dahuang-Codes dauert 100 Millisekunden und belegt 5 MB Speicher. Die einmalige Ausführung des Codes von Xiao Hui dauert 100 Sekunden und belegt 500 MB Speicher. Also...


Es ist ersichtlich, dass die Messung der Codequalität zwei sehr wichtige Indikatoren umfasst:
1. Laufzeit;
2.



Grundoperationen Anzahl der Ausführungen
Bezüglich der Anzahl der Ausführungen grundlegender Operationen des Codes verwenden wir vier Szenen im Leben als Analogie:
Szenario 1:Geben Sie Xiao Hui alle 3 Tage einen 10-Zoll-Laib Brot.

Die Antwort lautet natürlich 3 x 10 = 30 Tage.
Was ist, wenn die Länge des Brotes N Zoll beträgt?
Es wird zu diesem Zeitpunkt 3 x n = 3n Tage dauern, das gesamte Brot zu essen.
Wenn eine Funktion verwendet wird, um diese relative Zeit auszudrücken, kann sie als T(n) = 3n aufgezeichnet werden.
Szene 2: Gib Xiao Hui alle 5 Tage einen 16-Zoll-Laib Brot. Beim ersten Mal isst er 8 Zoll Beim zweiten Mal fielen 4 Zoll ab und beim dritten Mal wurden 2 Zoll gegessen ... Wie viele Tage wird es also dauern, bis Xiao Hui nur 1 Zoll Brot gegessen hat?
Um diese Frage zu übersetzen, wird die Zahl 16 fortlaufend durch 2 geteilt. Wie oft wird das Ergebnis gleich 1 sein? Dabei handelt es sich um Logarithmen in der Mathematik. Der Logarithmus von 16 zur Basis 2 kann als log16 abgekürzt werden.
Daher dauert es 5 x log16 = 5 x 4 = 20 Tage, um nur 1 Zoll Brot zu essen.
Was ist, wenn die Länge des Brotes N Zoll beträgt?
Es dauert 5 x logn = 5logn Tage, aufgezeichnet als T(n) = 5logn.
Szene 3: Gib Xiao Hui ein 10-Zoll-Stück Brot und eine Hähnchenkeule. Xiao Hui isst alle 2 Tage eine Hähnchenkeule. Wie viele Tage braucht Xiao Hui, um die ganze Hähnchenkeule zu essen?

Die Antwort ist natürlich 2 Tage. Weil ich nur gesagt habe, dass ich Hähnchenschenkel esse, was nichts mit dem 10-Zoll-Brot zu tun hat.
Was ist, wenn die Länge des Brotes N Zoll beträgt?
Egal wie lang das Brot ist, die Zeit, die zum Verzehr der Hähnchenschenkel benötigt wird, beträgt immer noch 2 Tage, aufgezeichnet als T(n) = 2.
Szene 4: Geben Sie Xiao Hui einen 10-Zoll-Laib Brot. Xiao Hui braucht 1 Tag, um den ersten Zoll zu essen, 2 Tage, um den zweiten Zoll zu essen, und 2 Tage, um den zu essen Es dauert drei Tage, einen Zentimeter zu fressen... Für jeden weiteren Zentimeter braucht man einen weiteren Tag. Wie viele Tage braucht Xiao Hui, um das ganze Brot zu essen?
Die Antwort ist die Summe von 1 bis 10, also 55 Tage.
Was ist, wenn die Länge des Brotes N Zoll beträgt?
Um zu diesem Zeitpunkt das ganze Brot zu essen, braucht man 1+2+3+......+ n-1 + n = (1+n)*n/2 = 0,5n^2 + 0,5n .
Aufgezeichnet als T(n) = 0,5n^2 + 0,5n.

Das Obige ist die relative Zeit, die mit dem Essen verbracht wird. Diese Idee gilt auch für die Statistik der Anzahl der Grundoperationen des Programms. Die vier Szenarien entsprechen gerade den vier häufigsten Ausführungsmethoden im Programm:
Szenario 1: T(n) = 3n, die Anzahl der Ausführungen ist linear.
void eat1(int n){
for(int i=0; i<n; i++){;
System.out.println("等待一天");
System.out.println("等待一天");
System.out.println("吃一寸面包");
}
}
voSzenario 2: T(n) = 5logn, die Anzahl der Ausführungen ist logarithmisch.
void eat2(int n){
for(int i=1; i<n; i*=2){
System.out.println("等待一天");
System.out.println("等待一天");
System.out.println("等待一天");
System.out.println("等待一天");
System.out.println("吃一半面包");
}
}Szenario 3: T(n) = 2, die Anzahl der Ausführungen ist konstant.
void eat3(int n){
System.out.println("等待一天");
System.out.println("吃一个鸡腿");
}Szenario 4: T(n) = 0,5n^2 + 0,5n, die Anzahl der Ausführungen ist ein Polynom.
void eat4(int n){
for(int i=0; i<n; i++){
for(int j=0; j<i; j++){
System.out.println("等待一天");
}
System.out.println("吃一寸面包");
}
}

Asymptotische Zeitkomplexität
Mit Können wir anhand der Funktion T(n) der Anzahl der Ausführungszeiten grundlegender Operationen die Laufzeit eines Codeabschnitts analysieren und vergleichen? Es gibt immer noch gewisse Schwierigkeiten.
Zum Beispiel ist die relative Zeit von Algorithmus A T(n) = 100n und die relative Zeit von Algorithmus B ist T(n) = 5n^2. Welcher der beiden hat eine längere Laufzeit? Dies hängt vom Wert von n ab.
Zu diesem Zeitpunkt gibt es also das Konzept der asymptotischen Zeitkomplexität (asymptotische Zeitkomplexität). Die offizielle Definition lautet wie folgt:
Wenn es eine Funktion f(n) gibt, z dass, wenn n sich der Unendlichkeit nähert. Wenn der Grenzwert von T(n)/f(n) eine Konstante ungleich Null ist, dann wird f(n) als Funktion derselben Größenordnung wie T(n) bezeichnet. .
Mit T(n) = O(f(n)) bezeichnet, wird O(f(n)) als asymptotische Zeitkomplexität des Algorithmus oder kurz Zeitkomplexität bezeichnet.
Asymptotische Zeitkomplexität wird durch ein großes O dargestellt und wird daher auch als Big-O-Notation bezeichnet.


Wie leitet man die Zeitkomplexität ab? Es gibt folgende Prinzipien:
Wenn die Laufzeit eine konstante Größe hat, verwenden Sie eine konstante 1, um sie darzustellen;
Behalten Sie nur den Term höchster Ordnung in der Zeitfunktion bei.
Wenn der Term höchster Ordnung vorhanden ist, wird der Koeffizient vor dem Term höchster Ordnung weggelassen.
Lassen Sie uns gerade auf die vier Szenen zurückblicken.
Szenario 1:
T(n) = 3n
Der Term höchster Ordnung ist 3n, wobei der Koeffizient 3 und die Umrechnung weggelassen werden Zeit Die Komplexität ist:
T(n) = O(n)
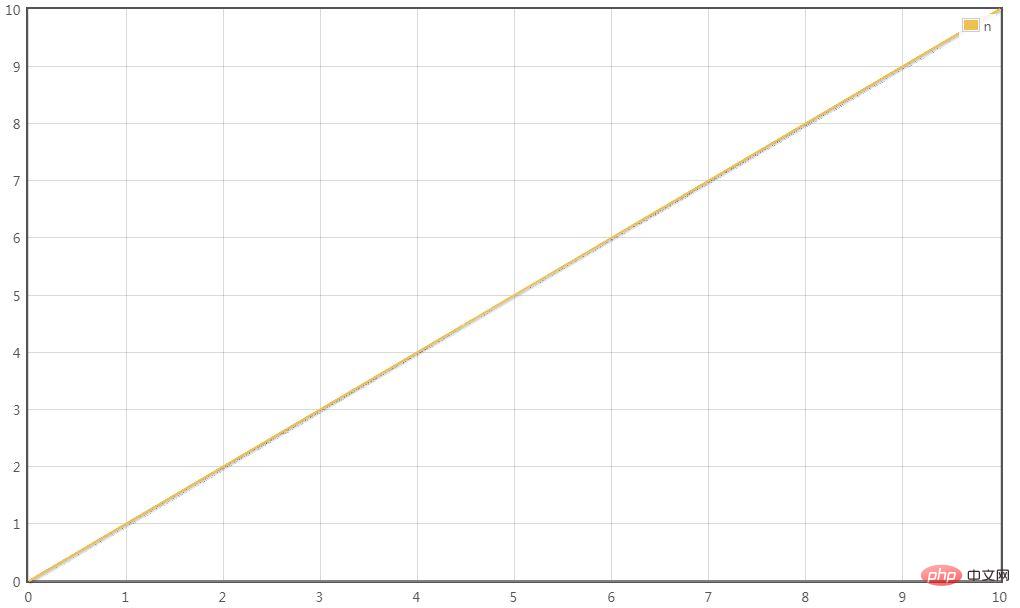
Szenario 2:
T (n) = 5logn
Der Term höchster Ordnung ist 5logn, ohne den Koeffizienten 5 beträgt die zeitliche Komplexität der Transformation:
T (n) = O (logn)
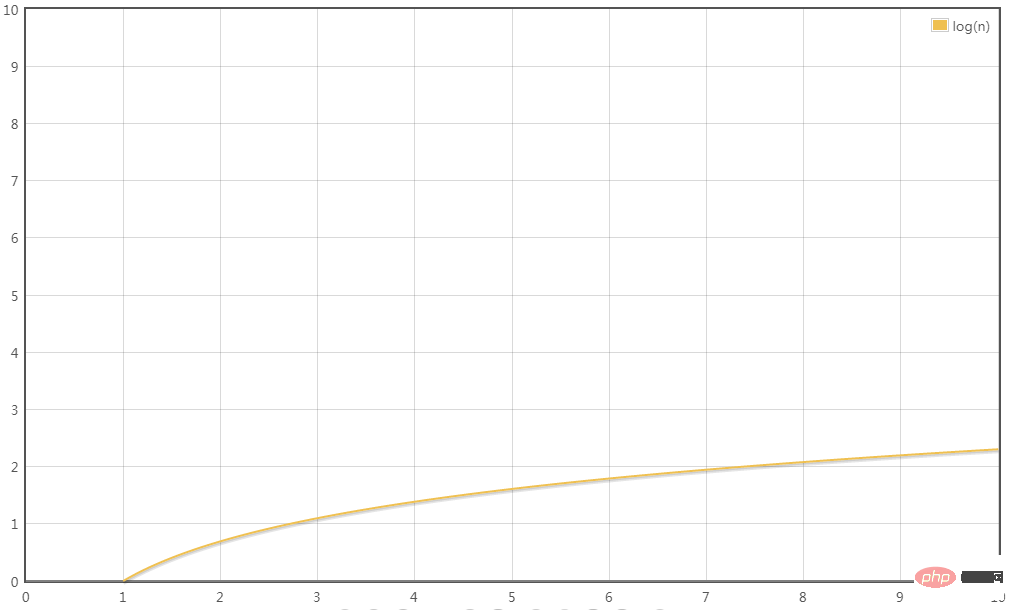
Szenario 3:
T(n) = 2
ist nur von konstanter Größe und die zeitliche Komplexität von Die Transformation ist:
T(n) = O(1)
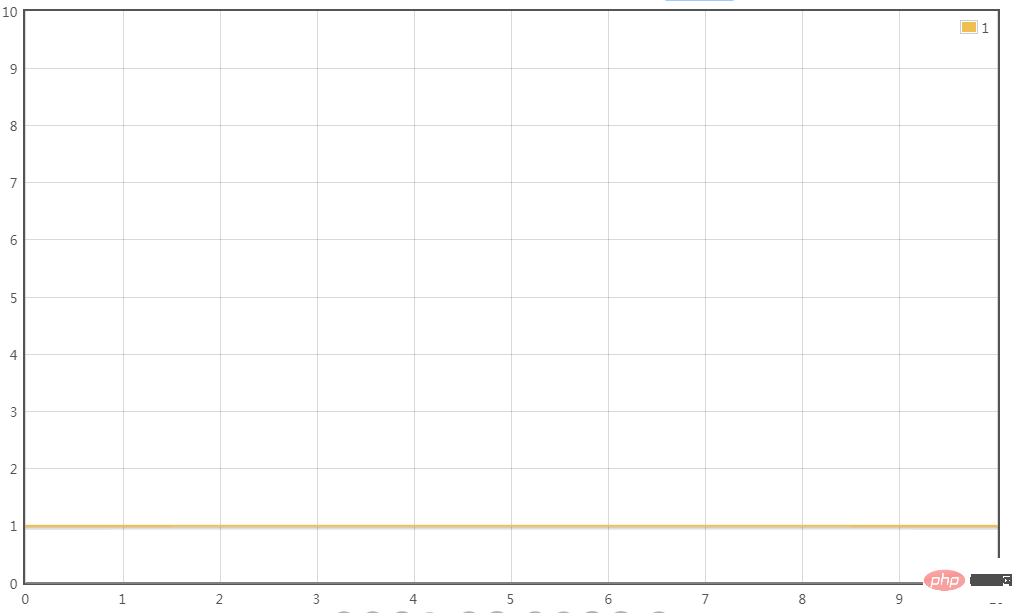
Szenario 4:
T (n) = 0,5n^ 2 + 0,5n
Der Term höchster Ordnung ist 0,5n^2, ohne den Koeffizienten 0,5 beträgt die zeitliche Komplexität der Transformation:
T(n) = O(n^2)
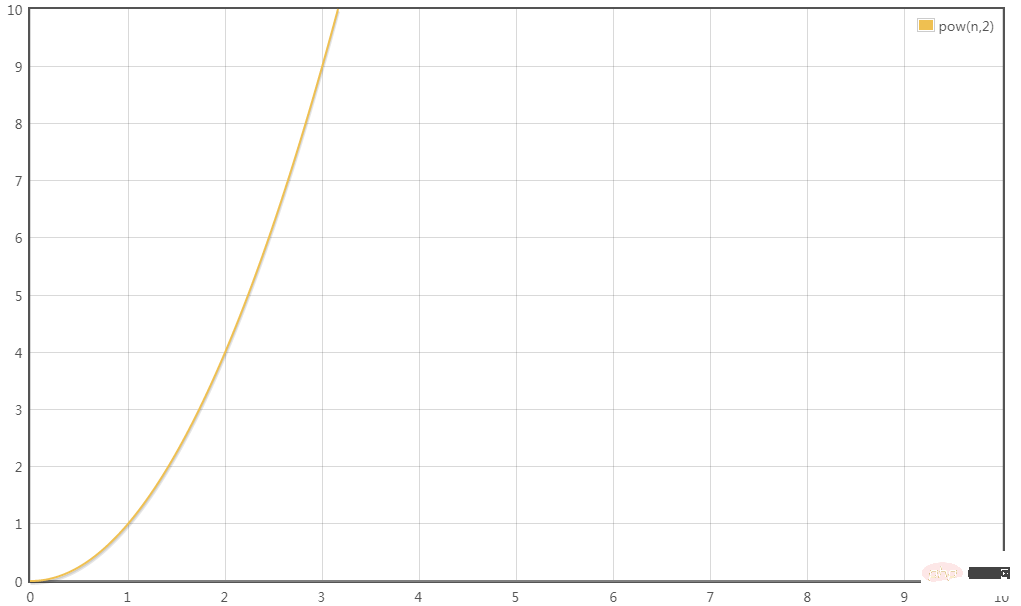
Welche dieser vier zeitlichen Komplexitäten dauert länger und wer spart Zeit? Nach ein wenig Nachdenken können Sie zu dem Schluss kommen:
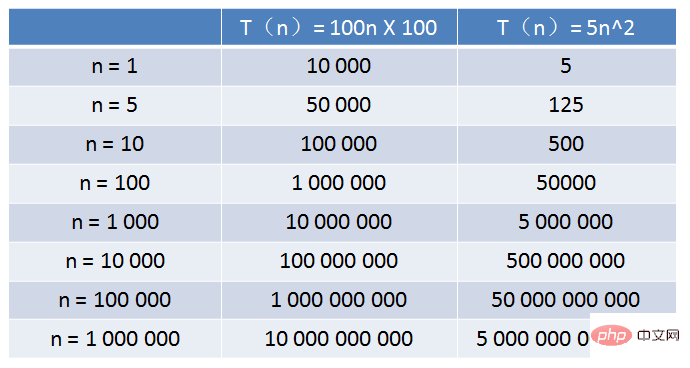
O(1) Im Welt der Programmierung Zusätzlich zu den oben genannten vier Szenarien gibt es viele verschiedene Formen der Zeitkomplexität, wie zum Beispiel: O(nlogn), O(n^3), O(m*) n ), O(2^n), O(n!) Wenn wir in Zukunft durch den Ozean des Codes reisen, werden wir weiterhin auf Algorithmen mit der oben genannten Zeitkomplexität stoßen. Riesiger Unterschied in der Zeitkomplexität Lassen Sie uns ein Beispiel geben: Die relative Zeitskala von Algorithmus A ist T(n) = 100n, und die Zeitkomplexität ist O(n) Die relative Zeit von Algorithmus B Die Skala ist T(n) = 5n^2 und die Zeitkomplexität ist O(n^2) Algorithmus A läuft auf einem alten Computer bei Xiao Hui zu Hause und Algorithmus B läuft auf einem bestimmten Supercomputer. Die Laufgeschwindigkeit ist 100-mal höher als bei alten Computern. Welcher der beiden Algorithmen läuft also schneller, wenn die Eingabegröße n zunimmt? Wie aus der Tabelle ersichtlich ist, ist die Laufzeit von Algorithmus A viel länger als die von Algorithmus B, wenn der Wert von n sehr klein ist von n etwa 1000 erreicht. Die Laufzeiten von Algorithmus A und Algorithmus B liegen nahe beieinander und langsamer, und die Lücke wird immer offensichtlicher. Dies ist der Unterschied, der durch unterschiedliche Zeitkomplexitäten verursacht wird. Wenn Sie weitere technische Tutorials erfahren möchten, achten Sie bitte unbedingt auf die PHP-Chinese-Website! 




Das obige ist der detaillierte Inhalt vonEine Reihe von Diagrammen von Datenstrukturen, die Ihnen helfen, die Zeitkomplexität zu verstehen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

