Einführung in die Java-Zirkelwarteschlange (Codebeispiel)

Dieser Artikel bietet Ihnen eine Einführung in Java-Zirkelwarteschlangen (Codebeispiele). Ich hoffe, dass er für Sie hilfreich ist.

Um die durch Array-Warteschlangen verursachten Probleme zu lösen, stellt Ihnen dieser Artikel kreisförmige Warteschlangen vor.

Illustration der Ideenanalyse

Oh mein Wort, denn der Autor ist nicht sehr gut darin, den geposteten Bildern Animationseffekte wie Verschieben oder Löschen zu verleihen Elemente (schließlich ist dies für alle intuitiver). Der Autor kann Ihnen hier nur durch statische Bilder helfen, das Implementierungsprinzip zu verstehen. Wenn jemand weiß, wie es geht, teilen Sie uns bitte Ihre Weisheit mit Kommentarbereich.

Hier deklarieren wir ein Array mit einer Kapazität von 8 und markieren den Index 0-7 und verwenden dann front und tail, um die Warteschlange, den Kopf und das Ende der Warteschlange darzustellen ; im Bild unten zeigen die Positionen von front und tail zunächst auf die Position von Index 0, was bedeutet, dass jeder dies im Hinterkopf behalten muss, wenn front == tai die <font color="'red'"></font>Warteschlange leer ist um die kritischen Bedingungen zu unterscheiden, wenn die Warteschlange fast voll ist, was später vorgestellt wird

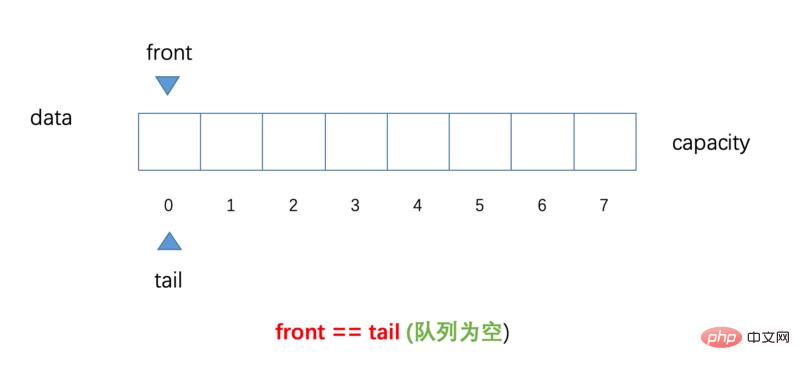
Damit jeder den folgenden Inhalt besser verstehen kann, habe ich hier werde es kurz erklären

front: Stellt den Kopf der Warteschlange dar und zeigt immer auf das erste Element in der Warteschlange (wenn die Warteschlange leer ist, zeigt vorne auf die Position mit Index 0)

tail: Stellt das Ende der Warteschlange dar und zeigt immer auf die nächste Position des letzten Elements in der Warteschlange.

Elemente gelangen in die Warteschlange, behalten die Position von tail bei Führen Sie tail++-Operationen aus und führen Sie an der Position

die Operation

durch. Wenn Elemente in die Warteschlange gestellt und aus der Warteschlange entfernt werden, handelt es sich lediglich um eine ++-Operation Behalten Sie die Positionen von front und front++ bei. Dies ist eigentlich nicht streng, die richtige Position für die Beibehaltung des Hecks sollte (Heck + 1) % Kapazität sein Deshalb wird es eine zirkuläre Warteschlange genannt. Ich werde es jetzt nicht erklären, wenn Sie es verstehen, ich glaube, dass es später jeder weiß. tailfrontLassen Sie uns einen Blick darauf werfen, ob sich nun ein Element a der Warteschlange anschließt, dem aktuellen Diagramm:

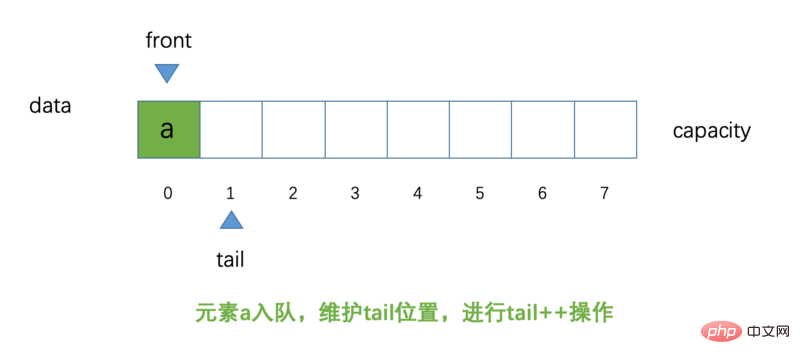Wir sehen jetzt, dass Element a der Warteschlange beitritt, our Die Position, auf die tail zeigt, hat sich geändert und die ++-Operation wurde ausgeführt, aber die Position von front hat sich nicht geändert und zeigt immer noch auf die Position mit Index 0. Denken Sie daran, was der Autor oben gesagt hat: Die Position von front zeigt immer auf die erste Position in der Warteschlange. Die Position des Schwanzes zeigt immer auf die nächste Position des letzten Elements in der Warteschlange

Fügen wir nun noch ein paar Elemente b, c, d, e hinzu Die Warteschlange. Schauen Sie sich das damalige schematische Diagramm an:

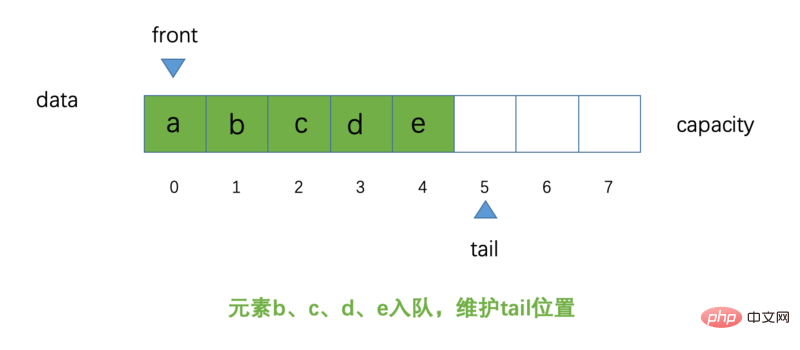Ich glaube, jeder weiß, dass das schematische Diagramm so ist, es scheint, dass es solche gibt nicht viele Änderungen (bitte machen Sie sich keine Sorgen, der Autor hat es auch für alle einfacher gemacht, zu verstehen, was genau eine kreisförmige Warteschlange ist? Bitte verzeihen Sie mir O(∩_∩)O! )

Nachdem ich nachgeschaut habe Werfen wir einen Blick auf die Operation, in der Elemente in die Warteschlange gelangen. Wie sieht die Operation aus, wenn Elemente aus der Warteschlange entfernt werden?

Element

ist aus der Warteschlange entfernt. Das schematische Diagramm sieht wie folgt aus:

a

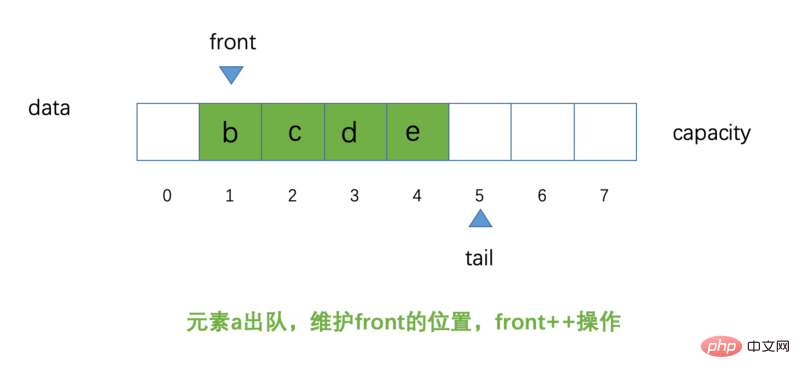Jetzt wurde Element a aus der Warteschlange entfernt und die Position von vorne zeigt auf den Index 1 Position, jetzt müssen nicht mehr alle Elemente im Array eine Position nach vorne verschoben werden

Dies ist dasselbe wie unsere Array-Warteschlange (unsere Array-Warteschlange erfordert, dass Elemente aus der Warteschlange entfernt werden, und nachfolgende Elemente müssen dies tun eine Position nach vorne verschieben) Völlig anders, wir müssen nur die Richtung der Front ändern. Die vorherige O(n)-Operation ist zu einer O(1)-Operation geworden

Wir entfernen Element b wieder aus der Warteschlange, Der Schaltplan Das Diagramm lautet wie folgt:

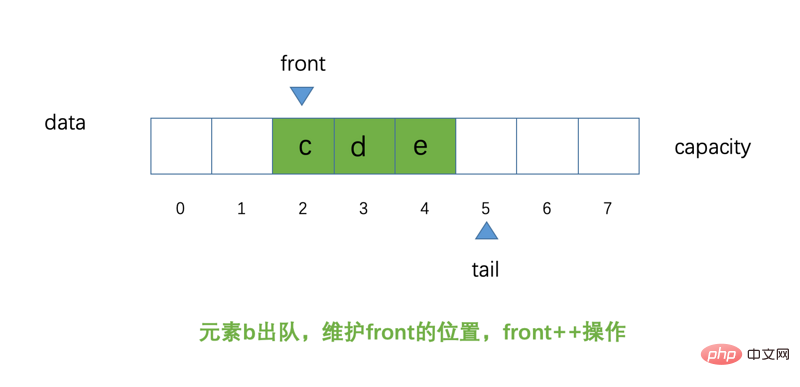An dieser Stelle fragen sich einige Freunde vielleicht, warum es eine kreisförmige Warteschlange heißt? Versuchen wir es nun. Das schematische Diagramm sieht zu diesem Zeitpunkt wie folgt aus:

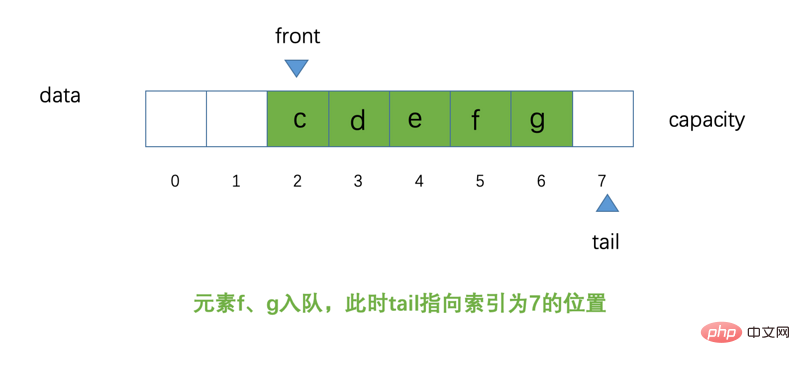
Es gibt immer noch keine Änderung Wenn wir zu diesem Zeitpunkt ein weiteres Element h zur Warteschlange hinzufügen, stellt sich die Frage: Wie soll die Position unseres Schwanzes sein? Das schematische Diagramm sieht wie folgt aus:

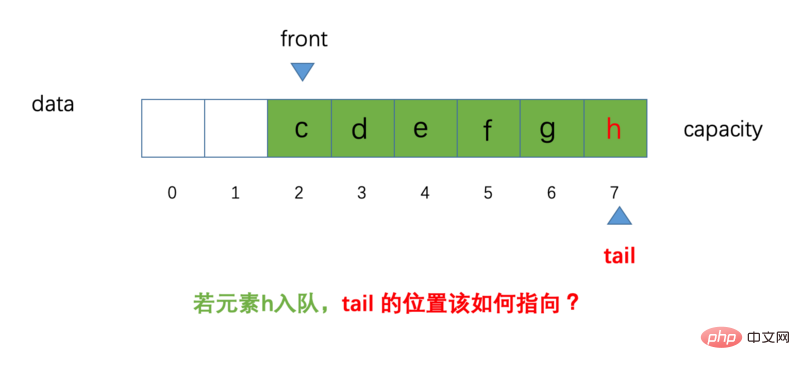
Nach dem, was wir zuvor gesagt haben, werden Elemente in die Warteschlange gestellt: Behalten Sie die Position des Schwanzes bei und führen Sie den Schwanz++-Vorgang aus. Zu diesem Zeitpunkt hat unser Schwanz auf die Position mit Index 7 gezeigt. Wenn wir Es ist offensichtlich unmöglich, eine ++-Operation am Ende (Array außerhalb der Grenzen) durchzuführen.

Aufmerksame Freunde werden feststellen, dass unsere Warteschlange zu diesem Zeitpunkt nicht voll ist und noch zwei Positionen übrig sind (dies liegt daran, dass nach unserem Elemente werden aus der Warteschlange entfernt), der aktuelle Platz wird nicht durch nachfolgende Elemente verdrängt), Sie können sich unser Array als Ring vorstellen, dann ist die Position nach Index 7 Index 0

Wie können wir aus der Position des Index berechnen? 7 An der Position von Index 0 haben wir bereits über Tail++-Operationen gesprochen. Der Autor hat zu Beginn auch darauf hingewiesen, dass dies nicht streng ist. Es sollte (Tail + 1) % Kapazität sein, was zu (7 + 1) % wird. 8 entspricht 0.

Wenn wir also zu diesem Zeitpunkt Element h in die Warteschlange aufnehmen lassen, zeigt unser Schwanz auf die Position mit dem Index 0. Das schematische Diagramm sieht wie folgt aus:

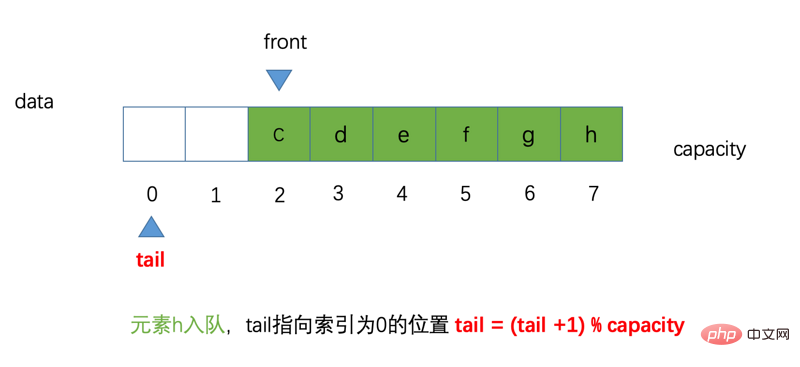
Angenommen, dass nun ein neues Element k zur Warteschlange hinzugefügt wird, dann ist die Position von tail gleich (tail + 1) % Kapazität, also (0 + 1) % 8 entspricht 1, was auf die Position mit Index 1 zeigt

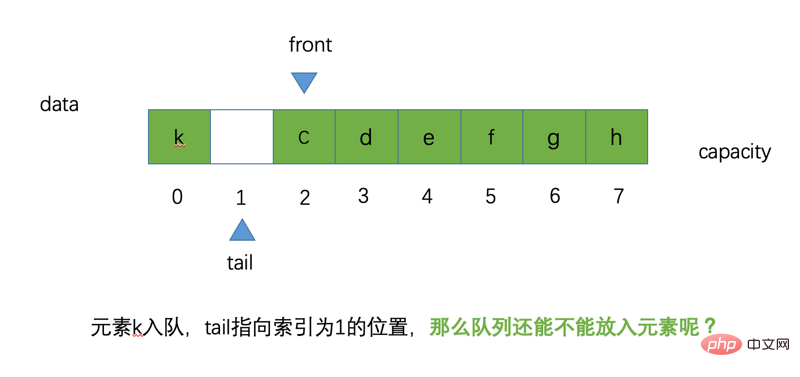
Dann stellt sich die Frage: Kann unsere kreisförmige Warteschlange weiterhin Elemente in die Warteschlange stellen? Lassen Sie es uns analysieren. Das Bild zeigt, dass wir immer noch eine leere Raumposition mit Index 0 haben, die zu diesem Zeitpunkt die Position ist, auf die tail zeigt.

Gemäß der vorherigen Logik wird davon ausgegangen, dass ein neues Element eingefügt werden kann Jetzt führt unser Schwanz eine Kapazitätsberechnung (Schwanz +1) % durch und das Ergebnis ist 2 (wenn das Element erfolgreich zur Warteschlange hinzugefügt wurde, ist die Warteschlange zu diesem Zeitpunkt voll). Zu diesem Zeitpunkt stellen wir fest, dass die Vorderseite den Kopf darstellt der Warteschlange zeigt auch auf die Position mit Index 2

Wenn das neue Element erfolgreich zur Warteschlange hinzugefügt wurde, ist unser Schwanz auch gleich 2, dann wird er zu tail == front. Zu Beginn haben wir das erwähnt wenn die Warteschlange leer ist, tail == front, was nun? Wenn tail auch gleich front ist, wenn die Warteschlange voll ist, können wir nicht zwischen Sammlung, wenn die Warteschlange voll ist, und Sammlung, wenn die Warteschlange leer ist

Daher verschwenden wir in der kreisförmigen Warteschlange immer einen Platz. Um zu unterscheiden, wann die Warteschlange voll ist und wann die Warteschlange leer ist, dh wenn (tail + 1) % Kapazität == vorne, bedeutet dies, dass die Warteschlange ist voll, und wenn front == tail bedeutet, dass die Warteschlange leer ist.

Nachdem wir das Implementierungsprinzip der zirkulären Warteschlange verstanden haben, implementieren wir es mit Code.

Code-Implementierung

Schnittstellendefinition: Queue

public interface Queue<e> {
    /**
     * 入队
     *
     * @param e
     */
    void enqueue(E e);

    /**
     * 出队
     *
     * @return
     */
    E dequeue();

    /**
     * 获取队首元素
     *
     * @return
     */
    E getFront();

    /**
     * 获取队列中元素的个数
     *
     * @return
     */
    int getSize();

    /**
     * 判断队列是否为空
     *
     * @return
     */
    boolean isEmpty();
}</e>

Schnittstellenimplementierung: LoopQueue

public class LoopQueue<e> implements Queue<e> {
    /**
     * 承载队列元素的数组
     */
    private E[] data;
    /**
     * 队首的位置
     */
    private int front;
    /**
     * 队尾的位置
     */
    private int tail;
    /**
     * 队列中元素的个数
     */
    private int size;

    /**
     * 指定容量，初始化队列大小
     * (由于循环队列需要浪费一个空间，所以我们初始化队列的时候，要将用户传入的容量加1)
     *
     * @param capacity
     */
    public LoopQueue(int capacity) {
        data = (E[]) new Object[capacity + 1];
    }

    /**
     * 模式容量，初始化队列大小
     */
    public LoopQueue() {
        this(10);
    }


    @Override
    public void enqueue(E e) {
        // 检查队列为满
        if ((tail + 1) % data.length == front) {
            // 队列扩容
            resize(getCapacity() * 2);
        }
        data[tail] = e;
        tail = (tail + 1) % data.length;
        size++;
    }


    @Override
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        // 出队元素
        E element = data[front];
        // 元素出队后，将空间置为null
        data[front] = null;
        // 维护front的索引位置(循环队列)
        front = (front + 1) % data.length;
        // 维护size大小
        size--;

        // 元素出队后，可以指定条件，进行缩容
        if (size == getCapacity() / 2 && getCapacity() / 2 != 0) {
            resize(getCapacity() / 2);
        }
        return element;
    }

    @Override
    public E getFront() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        return data[front];
    }

    @Override
    public int getSize() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return front == tail;
    }


    // 队列快满时，队列扩容；元素出队操作，指定条件可以进行缩容
    private void resize(int newCapacity) {
        // 这里的加1还是因为循环队列我们在实际使用的过程中要浪费一个空间
        E[] newData = (E[]) new Object[newCapacity + 1];
        for (int i = 0; i <p>Testklasse: LoopQueueTest</p>
<pre class="brush:php;toolbar:false">public class LoopQueueTest {
    @Test
    public void testLoopQueue() {
        LoopQueue<integer> loopQueue = new LoopQueue();
        for (int i = 0; i <h5>Testergebnisse: </h5>
<pre class="brush:php;toolbar:false">原始队列: LoopQueue{【队首】data=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=0, tail=10, size=10, capacity=10}
元素0出队: LoopQueue{【队首】data=[null, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=1, tail=10, size=9, capacity=10}
元素1出队: LoopQueue{【队首】data=[null, null, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=2, tail=10, size=8, capacity=10}
元素2出队: LoopQueue{【队首】data=[null, null, null, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=3, tail=10, size=7, capacity=10}
元素3出队: LoopQueue{【队首】data=[null, null, null, null, 4, 5, 6, 7, 8, 9, null]【队尾】, front=4, tail=10, size=6, capacity=10}
元素4出队,发生缩容: LoopQueue{【队首】data=[5, 6, 7, 8, 9, null]【队尾】, front=0, tail=5, size=5, capacity=5}
队首元素：5

Vollversionscode GitHub-Repository-Adresse: Java-Versionsdatenstrukturwarteschlange (zirkuläre Warteschlange)

Dieser Artikel endet hier Das ist Weitere spannende Inhalte finden Sie in der Spalte Java Video Tutorial auf der chinesischen PHP-Website!

Das obige ist der detaillierte Inhalt vonEinführung in die Java-Zirkelwarteschlange (Codebeispiel). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!