Heim >Web-Frontend >js-Tutorial >Darstellungsbereich von Gleitkommazahlen
Darstellungsbereich von Gleitkommazahlen
- 清浅Original
- 2019-03-08 15:57:2237826Durchsuche
Gleitkommazahlen bestehen aus drei Teilen: Symbol, Exponentencode und Mantisse. Gleitkommazahlen werden in Gleitkommazahlen mit einfacher Genauigkeit und Gleitkommazahlen mit doppelter Genauigkeit unterteilt Zahlen beträgt -3,4E38 ~3,4E38, der Bereich der Gleitkommazahlen mit doppelter Genauigkeit beträgt -1,79E+308 ~ +1,79E+308
[Empfohlen Kurs: JavaScript-Tutorial】
Darstellung von Gleitkommazahlen
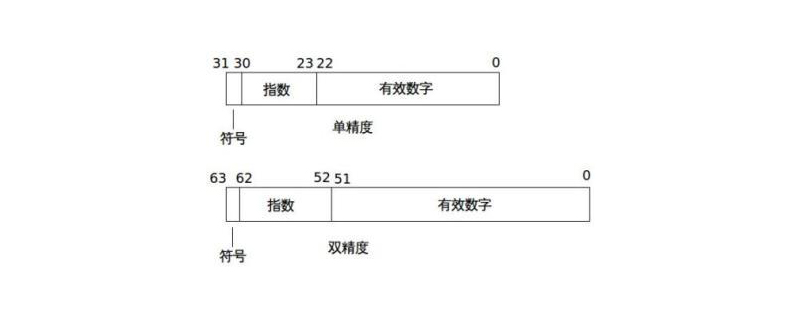
Eine Gleitkommazahl (Floating Point Number) besteht aus drei Grundkomponenten : Vorzeichen (Sign), Expand Code ( Exponent) und Mantisse (Mantissa). Gleitkommazahlen können normalerweise im folgenden Format dargestellt werden:
| S | P | M |
wobei S das Vorzeichenbit, P der Exponentencode und M die Mantisse ist.
Gemäß der Definition im IEEE (Institute of Electrical and Electronics Engineers) 754-Standard sind Gleitkommazahlen mit einfacher Genauigkeit 32 Bit (d. h. 4 Bytes) und Gleitkommazahlen mit doppelter Genauigkeit 64-Bit (d. h. 8 Bytes) von. Die Anzahl der von S, P und M belegten Ziffern und die Darstellungsmethode der beiden sind in der folgenden Tabelle aufgeführt:
|
S | P | M td> | Formel darstellen | Offset | ||||||||||||||||||
| 1 (31. Position) | 8 (Ziffern 30 bis 23) | 23 (Ziffern 22 bis 0) | (-1)^S*2(P-127)*1.M | 127 | |||||||||||||||||||
| Gleitkommazahl mit doppelter Genauigkeit | 1 (63. Position) | 11 ( 62 bis 52 Bit) | 52 (51 bis 0 Bits) | (-1)^S*2(P -1023)* 1.M | 1023 |
wobei S das Vorzeichenbit ist, nur 0 und 1, was jeweils positiv und negativ anzeigt
P ist der Exponentencode, der normalerweise durch Rahmencode dargestellt wird (Rahmencode und Komplementcode haben nur das entgegengesetzte Vorzeichenbit, Der Rest ist derselbe. Für positive Zahlen sind der ursprüngliche Code, das Komplement und das Komplement gleich; für negative Zahlen ist das Komplement die Umkehrung aller ursprünglichen Codes ihrer Absolutwerte und die anschließende Addition von 1). Der Exponentencode kann eine positive oder eine negative Zahl sein. Um den Fall eines negativen Exponenten zu handhaben, muss der tatsächliche Exponentenwert mit einem Bias-Wert als dem im Exponentenfeld gespeicherten Wert addiert werden Der Abweichungswert der Zahl mit einfacher Genauigkeit beträgt 127, der Abweichungswert der Zahl mit doppelter Genauigkeit beträgt 1023. Beispielsweise wird der tatsächliche Exponentenwert 0 mit einfacher Genauigkeit als 127 im Exponentenfeld gespeichert, während 64 im Exponentenfeld den tatsächlichen Exponentenwert -63 darstellt. Die Einführung des Bias ermöglicht Zahlen mit einfacher Genauigkeit Drücken Sie tatsächlich den Exponentenwert aus. Der Bereich beträgt -127 bis 128 (beide Enden eingeschlossen).
M ist die Mantisse, wobei Zahlen mit einfacher Genauigkeit 23 Bit lang und Zahlen mit doppelter Genauigkeit 52 Bit lang sind. Der IEEE-Standard verlangt, dass Gleitkommazahlen kanonisch sein müssen. Dies bedeutet, dass die linke Seite des Dezimalpunkts der Mantisse 1 sein muss. Wenn Sie also die Mantisse speichern, kann die 1 vor dem Dezimalpunkt weggelassen werden, wodurch ein Binärbit frei wird, um mehr Mantissen zu speichern. Dabei wird tatsächlich ein 23-Bit langes Mantissenfeld verwendet, um die 24-Bit-Mantisse auszudrücken. Beispielsweise kann für Zahlen mit einfacher Genauigkeit die Binärzahl 1001,101 (entsprechend der Dezimalzahl 9,625) als 1,001101 × 23 ausgedrückt werden, sodass der tatsächlich im Mantissenfeld gespeicherte Wert 00110100000000000000000 ist, d. h. die 1 links vom Dezimalpunkt entfernt und rechts wird 0 verwendet.
Gemäß den Standardanforderungen müssen Werte, die nicht genau gespeichert werden können, auf den nächsten speicherbaren Wert gerundet werden, d. h. wenn er weniger als die Hälfte beträgt, wird er gerundet, und wenn er mehr als die Hälfte (einschließlich der Hälfte) beträgt ), wird gerundet. Für binäre Gleitkommazahlen gilt jedoch noch eine weitere Regel: Wenn der zu rundende Wert genau die Hälfte beträgt, wird nicht einfach gerundet, sondern der letzte der beiden speicherbaren Werte, die äquidistant nahe beieinander liegen Vorher und Nachher wird genommen. Die Anzahl der signifikanten Ziffern ist Null.
Gemäß der obigen Analyse definiert der IEEE 754-Standard den Darstellungsbereich von Gleitkommazahlen als:
| Binär | Dezimal | |||||||||
| Gleitkommazahl mit einfacher Genauigkeit | ± (2-2^-23) × 2127 | ~ ± 10^38.53 | |||||||||
| ± (2-2^-52) × 21023 | ~ ± 10^308.25 |
Die Darstellung von Gleitkommazahlen hat einen bestimmten Bereich. Wenn der Bereich überschritten wird, kommt es zu einem Überlauf (Flow). Im Allgemeinen werden Daten, die größer als der maximale Absolutwert sind, als Überlauf (Overflow) bezeichnet Der minimale absolute Wert wird als Unterlauf (Underflow) bezeichnet.
Darstellungskonventionen für Gleitkommazahlen
Gleitkommazahlen mit einfacher und doppelter Genauigkeit sind beide im IEEE 754-Standard definiert , und es gibt einige spezielle Konventionen, zum Beispiel:
1. Wenn P=0 und M=0, bedeutet es 0.
2. Wenn P = 255 und M = 0, bedeutet dies Unendlich, und das Vorzeichenbit wird verwendet, um zu bestimmen, ob es sich um positive Unendlichkeit oder negative Unendlichkeit handelt.
3. Wenn P=255 und M≠0, bedeutet das NaN (Not a Number, not a number).
Nicht standardmäßige Gleitkommazahlen
Wenn zwei Gleitkommazahlen mit extrem kleinen Absolutwerten subtrahiert werden, kann der Exponent der Differenz den zulässigen Bereich überschreiten und kann am Ende nur ungefähr 0 sein. Um solche Probleme zu lösen, hat der IEEE-Standard denormalisierte Gleitkommazahlen eingeführt, die festlegen, dass die Mantisse nicht normalisiert werden muss, wenn der Exponent einer Gleitkommazahl der minimal zulässige Exponentenwert ist. Bei nicht standardmäßigen Gleitkommazahlen wird die implizite Einschränkung des Mantissenbits aufgehoben und es können Gleitkommazahlen mit kleineren Absolutwerten gespeichert werden. Da es zudem nicht mehr durch das implizite Mantissenfeld eingeschränkt wird, besteht das oben erwähnte Problem extrem kleiner Unterschiede nicht, da alle speicherbaren Unterschiede zwischen Gleitkommazahlen auch gespeichert werden können.
Gemäß der Definition im IEEE 754-Standard kann der Darstellungsbereich kanonischer und nichtkanonischer Gleitkommazahlen wie folgt zusammengefasst werden:
|
Normale Gleitkommazahlen | Nicht standardmäßige Gleitkommazahl | Dezimaler ungefährer Bereich | ||||||||||||
| Gleitkommazahl mit einfacher Genauigkeit | ± 2^-149 bis (1-2^-23)*2^-126 | ± 2^-126 bis (2-2^-23)*2^127 | ± ~10^-44,85 bis ~10^38,53 | ||||||||||||
| Gleitkomma mit doppelter Genauigkeit number | ± 2^-1074 bis (1-2^- 52)*2^-1022 | ± 2^-1022 bis (2-2^-52)*2^1023 td> | ± ~10^-323,3 bis ~10^308,3 |
Standards im Zusammenhang mit IEEE 754
Die Schlussfolgerung daraus Der Artikel basiert auf dem IEEE 754-Standard. Bei diesem Standard handelt es sich um dezimale Gleitkommazahlen, es wird jedoch kein bestimmtes Format angegeben, weshalb es selten verwendet wird. Darüber hinaus begann im Jahr 2000 eine Überarbeitung des IEEE 754, bekannt als IEEE 754R, mit dem Ziel, die Standards IEEE 754 und IEEE 854 zu integrieren. Die Überarbeitungen des Gleitkommaformats dieses Standards umfassen: 1. Hinzufügen von 16-Bit- und 128-Bit-Binär-Gleitkommaformaten 2. Hinzufügen von Dezimal-Gleitkommaformaten und Übernahme des von IBM vorgeschlagenen Formats;
Zusammenfassung: Das Obige ist der gesamte Inhalt dieses Artikels, ich hoffe, er wird für alle hilfreich sein.
Das obige ist der detaillierte Inhalt vonDarstellungsbereich von Gleitkommazahlen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

