Grundlegende Methode zur Implementierung der binären Suche in Java (mit Code)

In diesem Artikel geht es um die grundlegende Methode zur Implementierung der binären Suche in Java (mit Code). Ich hoffe, dass er für Freunde hilfreich ist.

Die binäre Suche ist besonders einfach zu verstehen. Sie ähnelt der Divide-and-Conquer-Idee, die beim schnellen Sortieren und Zusammenführen verwendet wird. Jedes Mal wird die mittlere Zahl mit der Zielzahl verglichen und dann ermittelt ob es größer oder kleiner ist, und das Intervall wird halbiert.

Zum Beispiel:

Xiao Hong wählte eine Zahl von 1-100 (diese Zahl ist 56) und bat Xiao Ming zu erraten, was zu folgendem Dialog führte:

Xiao Ming Erste Schätzung: 68

Xiao Hong: Groß

Xiao Mings zweite Schätzung: 35

Xiao Hong: Klein

Xiao Mings dritte Schätzung Erste Schätzung: 58

Xiaohong: Zu groß

Xiao Mings vierte Vermutung: 49

Xiaohong: Klein

Xiao Mings fünfte Vermutung:54

Xiaohong: Zu klein

Xiao Mings sechste Schätzung: 56

Xiaohong: Bingo! ! !

Wir können sehen, dass Xiao Ming im obigen Gespräch das Intervall jedes Mal verkleinern kann, bis die Antwort richtig ist.

Die binäre Suche ist so. Zum Beispiel haben wir jetzt Arrays 8 , 11, 19 , 23, 27, 33, 45, 55, 67, 98, verwenden Sie die binäre Suche wie unten gezeigt: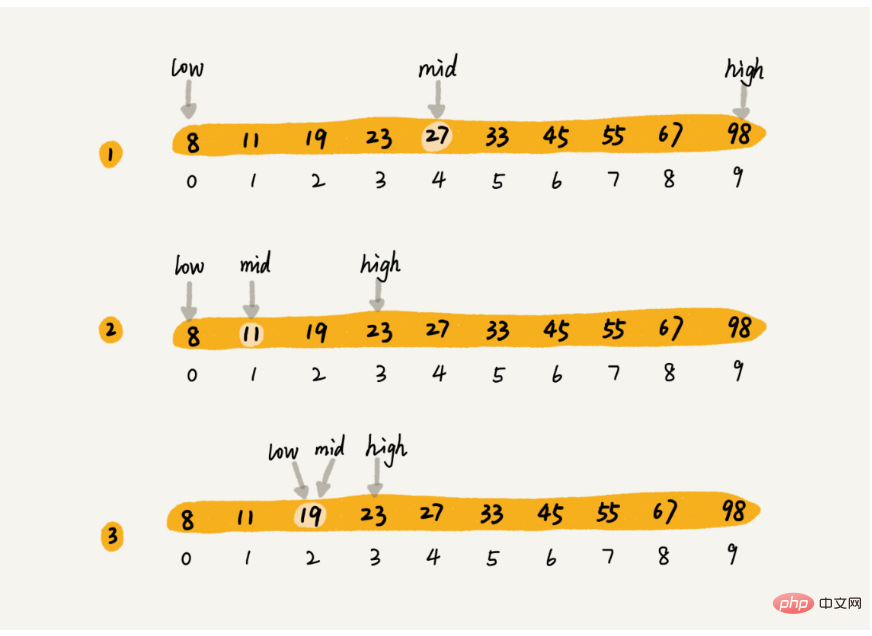

Jedes Mal, wenn Sie das Intervall um die Hälfte reduzieren können, können wir sehen, dass die Das Intervall ändert sich wie folgt:

Wenn die Intervallgröße unendlich nahe bei 1 liegt, ist k = log2n, sodass die Zeitkomplexität O(logn) ist.

Ist es besonders leicht zu verstehen? Hier ist eine einfache binäre Suche, die ich in Java implementiert habe (Hinweis: Es ist die einfachste Implementierung. Die Varianten der binären Suche sind sehr kompliziert und ich beherrsche sie noch nicht)

package com.structure.search;

/**
 * 二分查找法
 *
 * @author zhangxingrui
 * @create 2019-02-15 21:29
 **/
public class BinarySearch {

    public static void main(String[] args) {
        int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
        System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
        System.out.println(binarySearch(nums, 50004));
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-递归方式实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int p, int r, int k){
        if(p > r)
            return -1;

        int mid = (p + r) / 2;
        if(nums[mid] == k)
            return mid;

        if(k > nums[mid])
            return binarySearch(nums, mid + 1, r, k);
        else
            return binarySearch(nums, p,  mid - 1, k);
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-循环实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int k){
        int p = 0;
        int r = nums.length - 1;
        while (p <= r){
            int mid = (p + r) / 2;

            if(nums[mid] == k)
                return mid;

            if(k > nums[p])
                p = mid + 1;
            else
                r = mid - 1;
        }
        return -1;
    }

}

Der Code ist sehr einfach und es muss auf die Randbedingung p<=r geachtet werden.

Aus dem Code ist auch ersichtlich, dass die einfache Implementierung große Einschränkungen aufweist und nur auf geordnete Arrays ohne doppelte Daten angewendet werden kann.

Und die binäre Suche ist nicht für die Abfrage kleiner Daten geeignet (da eine Abfrage kleiner Daten nicht erforderlich ist). Dies ist gleichzeitig leicht zu verstehen und nicht für große Daten geeignet Frage, warum ist das Wollstoff?

Dies liegt an den oben genannten Gründen: Die binäre Suche eignet sich für die Verwendung von Arrays für die zugrunde liegenden Daten, aber das Array ist ein kontinuierlicher Speicherplatz. Wenn die Daten groß sind und Sie die binäre Suche verwenden möchten, ist dies der Fall Implementierung der Daten Nur

kann nur Arrays verwenden, was nicht sehr gut ist. Angenommen, meine Daten haben ein G, dann muss ich einen kontinuierlichen Speicherplatz von 1 G beantragen. Oh mein Gott, ich habe Angst, dass ich voll bin.

Das obige ist der detaillierte Inhalt vonGrundlegende Methode zur Implementierung der binären Suche in Java (mit Code). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!