Heim >Backend-Entwicklung >Python-Tutorial >Python implementiert die Monte-Carlo-Methode (Codebeispiel)
Python implementiert die Monte-Carlo-Methode (Codebeispiel)
- 不言nach vorne
- 2019-01-14 11:29:027063Durchsuche
Der Inhalt dieses Artikels befasst sich mit der Implementierung der Monte-Carlo-Methode (Codebeispiel) in Python. Ich hoffe, dass er für Freunde hilfreich ist.
Die Monte-Carlo-Methode ist eine von Neumann und Ulam vorgeschlagene statistische Simulationsmethode. Je mehr Zufallszahlen vorliegen, desto mehr Zufallszahlen ergeben die Ergebnisse genauer. Im Folgenden verwenden wir Python, um die Monte-Carlo-Methode zu implementieren.
1. Zuerst führen wir eine einfache Näherungsberechnung von Pi durch. In diesem Prozess müssen wir Zufallszahlen verwenden, also müssen wir zuerst import numpy as np verwenden, um die Numpy-Bibliothek zu importieren.
2. Code-Implementierung:
import numpy as np
total = 8000000
count = 0
for i in range(total):
x = np.random.rand()
y = np.random.rand()
dis = (x**2+y**2)**0.5
if dis <p>3. Im obigen Programm verwenden wir 8000000 Zufallszahlen für die Lieferung, damit das Ergebnis genauer ist, und es dauert eine gewisse Zeit Zeit, das Programm auszuführen. Das Endergebnis ist wie folgt: </p><p><span class="img-wrap"><img src="/static/imghwm/default1.png" data-src="https://img.php.cn//upload/image/549/675/172/1547436392667253.png" class="lazy" title="1547436392667253.png" alt="Python implementiert die Monte-Carlo-Methode (Codebeispiel)"></span></p>4. Das Bild unten ist ein Bild, das ich zufällig gezeichnet habe Im Zeichenwerkzeug können wir die Fläche des schwarzen Teils im Bild mithilfe der Monte-Carlo-Methode schätzen. <p></p><p style="max-width:90%"><span class="img-wrap"><img src="/static/imghwm/default1.png" data-src="https://img.php.cn//upload/image/583/174/740/1547436406520588.png" class="lazy" title="1547436406520588.png" alt="Python implementiert die Monte-Carlo-Methode (Codebeispiel)"></span></p>5. Das obige Diagramm ist unregelmäßig. Wir müssen nur wissen, dass die Zufallszahlen angezeigt werden, wenn eine große Anzahl von Zufallszahlen geworfen wird Berechnen Sie die Wahrscheinlichkeit des schwarzen Teils und multiplizieren Sie dann die Gesamtfläche, um die Fläche des schwarzen Teils abzuschätzen. Wir wissen, dass der schwarze RGB-Code (0,0,0) ist, daher müssen wir die Wahrscheinlichkeit von Zufallszahlen berechnen, wenn der RGB-Code (0,0,0) ist. <p></p>6. Code-Implementierung: <p></p><pre class="brush:php;toolbar:false">from PIL import Image
import numpy as np
im = Image.open("C:/Users/21974/Desktop/handwrite2.PNG")
total = 9000000
count = 0
defin = 0
width = im.size[0]
height = im.size[1]
for i in range(total): #用蒙特卡罗方法获得估计值
x = np.random.randint(0, width-1)
y = np.random.randint(0, height-1)
k = im.getpixel((x, y))
if k[0]+k[1]+k[2] == 0:
count += 1
print(int(width*height*count/total))
for i in range(width): #用遍历获得准确值
for j in range(height):
k = im.getpixel((i, j))
if k[0] + k[1] + k[2] == 0:
defin += 1
print(defin)Der obige Code kann in zwei Teile unterteilt werden, gefolgt vom geschätzten Wert der Fläche, der durch die Monte-Carlo-Methode erhalten wird for wird gefolgt von Es ist der genaue Wert der Fläche, die durch Durchlaufen aller Pixel erhalten wird, und vergleicht dann die beiden Ausgaben. 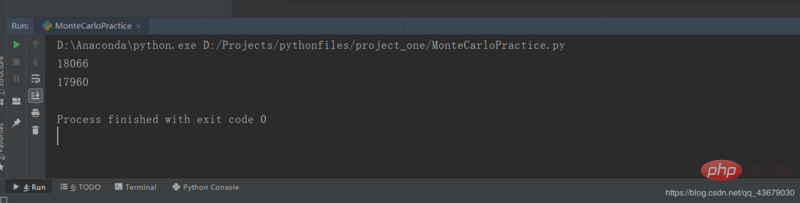
Das obige ist der detaillierte Inhalt vonPython implementiert die Monte-Carlo-Methode (Codebeispiel). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

