Heim >Web-Frontend >js-Tutorial >Einführung in Binärbäume (Binary Heaps) in JavaScript (Codebeispiele)
Einführung in Binärbäume (Binary Heaps) in JavaScript (Codebeispiele)
- 不言nach vorne
- 2019-01-08 10:11:285033Durchsuche
Dieser Artikel bietet Ihnen eine Einführung (Codebeispiel) zu Binärbäumen (Binärheaps). Ich hoffe, dass er Ihnen als Referenz dienen wird.
Binärbaum
Binärbaum ist eine Baumstruktur. Sie zeichnet sich dadurch aus, dass jeder Knoten höchstens zwei Zweigknoten hat Wurzelknoten, Zweigknoten und Blattknoten. Jeder Zweigknoten wird oft als Unterbaum bezeichnet.
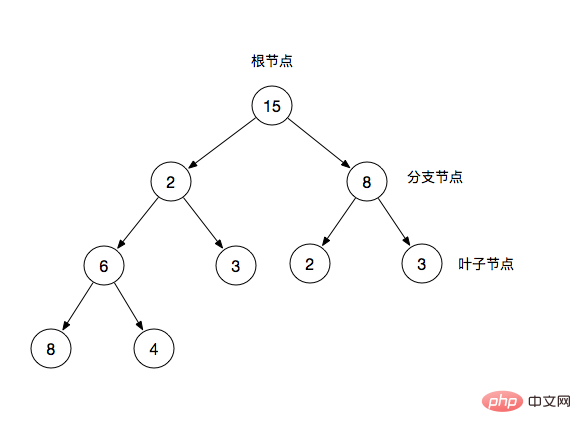
Wurzelknoten: der oberste Knoten des Binärbaums
Zweig Knoten: Zusätzlich zum Wurzelknoten und den Blattknoten
Blattknoten: Außer sich selbst gibt es keine anderen untergeordneten Knoten
Allgemeine Begriffe
In einem Binärbaum verwenden wir häufig übergeordnete Knoten und untergeordnete Knoten, um ihn zu beschreiben. Beispielsweise ist 2 im Bild der übergeordnete Knoten von 6 und 3 und umgekehrt 6 und 3 sind 2 untergeordnete Knoten
Drei Eigenschaften von Binärbäumen
Auf der i-ten Ebene eines Binärbaums gibt es at die meisten 2^i-1 Knoten
-
Wenn i=1, gibt es nur einen Wurzelknoten, 2^(i-1) = 2^0 = 1
Der Binärbaum mit Tiefe k ist höchstens Es gibt 2^k-1 Knoten
Wenn i=2, 2 ^k-1 = 2^2 - 1 = 3 Knoten
Für jeden Binärbaum T, wenn die Anzahl der Zusammenfassungspunkte n0 und die Anzahl der Knoten mit Grad 2 beträgt (Anzahl der Teilbäume ist 2) ist n2, dann ist n0=n2+1
Drei Hauptunterschiede zwischen Bäumen und Binärbäumen
Die Zahl Die Anzahl der Knoten eines Baums beträgt mindestens 1, während die Anzahl der Knoten eines Binärbaums 0 sein kann
Der maximale Grad (Anzahl der Knoten) eines Knotens in einem Baum beträgt nicht begrenzt, während der maximale Grad eines Knotens in einem Binärbaum 2 beträgt
Es gibt keine linke oder rechte Unterscheidung zwischen Knoten in einem Baum, während Knoten in linke und rechte Knoten unterteilt sind
Binärbaumklassifizierung
Binärbäume werden in vollständige Binärbäume und vollständige Binärbäume unterteilt
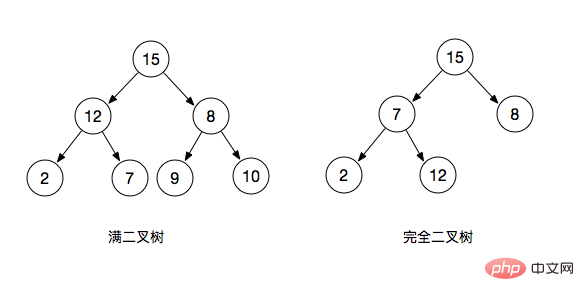
Vollständiger Binärbaum: Ein Binärbaum Ein Baum mit der Tiefe k und 2^k - 1 Knoten wird als vollständiger Binärbaum bezeichnet
Vollständiger Binärbaum: Ein vollständiger Binärbaum bezieht sich auf die letzte Ebene. Ein Binärbaum, in dem sich die linke Seite befindet ist voll, die rechte Seite kann voll sein oder nicht, und die verbleibenden Ebenen sind voll. Dies wird als vollständiger Binärbaum bezeichnet (ein vollständiger Binärbaum ist auch ein vollständiger Binärbaum)
Array-Darstellung des Binärbaums
Verwenden Sie ein Array, um die Struktur des Binärbaums darzustellen, beginnend vom Wurzelknoten nach oben Unten und von links nach rechts. In einem vollständigen Binärbaum, wie in der Abbildung unten gezeigt
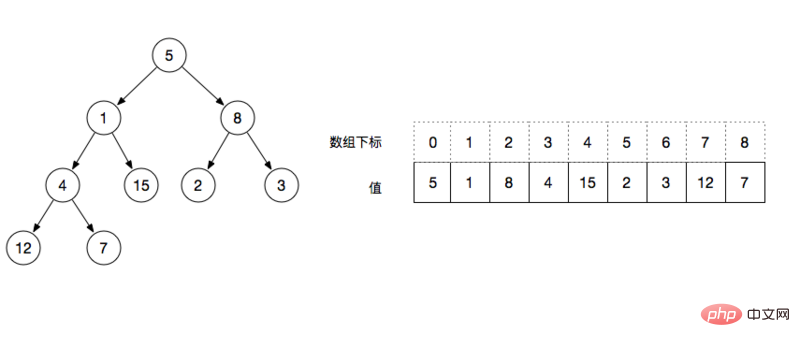
Anhand der obigen Abbildung können wir das vollständig analysieren Der durch das Array dargestellte Binärbaum hat die folgenden Eigenschaften:
-
left = index * 2 + 1, zum Beispiel: Der Index des Wurzelknotens ist 0, dann ist der Wert des linken Knotens ist das Indexarray[0*2+1]=1
right = index * 2 + 2, zum Beispiel: Der Index des Wurzelknotens ist 0, dann ist der Wert des Der rechte Knoten ist das tiefgestellte Array[0*2+2]=2
Ordinal>= floor(N/2) sind alle Blattknoten, zum Beispiel: floor(9/2) = 4, dann sind die Werte ab Index 4 Blattknoten
Binärer Heap
Die Struktur eines binären Heaps wird durch einen vollständigen Binärbaum dargestellt, der wird durch ein Array dargestellt, aber ein binärer Heap muss die folgenden Eigenschaften erfüllen:
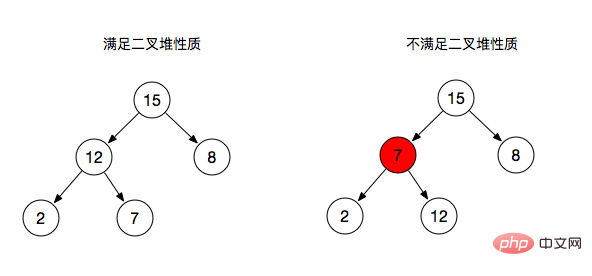
Der Schlüsselwert des übergeordneten Knotens eines binären Heaps ist immer größer oder gleich (kleiner als oder gleich) dem Schlüsselwert eines beliebigen untergeordneten Knotens
-
Wenn der Schlüssel des übergeordneten Knotens ist. Wenn der Wert größer oder gleich (kleiner oder gleich) dem Schlüsselwert von ist Jeder seiner untergeordneten Knoten wird max heap (min heap)

- Linkes Bild: Der übergeordnete Knoten ist immer größer oder gleich seinem untergeordneten Knoten erfüllt die Eigenschaften eines binären Heaps,
- Rechtes Bild: Zweigknoten 7, als übergeordneter Knoten von 2 und 12, erfüllt seine Eigenschaften nicht (größer oder gleich seinem untergeordneten Knoten). ).
- Einfügen: Knoten einfügen
- Löschen: Knoten löschen
- max-hepify: Verzweigungsknoten-Heap-Eigenschaften anpassen
- rebuildHeap: Den gesamten Binär-Heap neu erstellen
- Sortieren: Sortieren
- Initialisierung einer Array-Struktur
Speichern Sie die Array-Länge
class Heap{
constructor(arr){
this.data = [...arr];
this.size = this.data.length;
}
}
max-heapify maximale Heap-Operation
max-heapify dient dazu, jedes Element zu konvertieren, das nicht erfüllt die maximalen Heap-Eigenschaften Eine Operation zum Anpassen von Verzweigungsknoten.
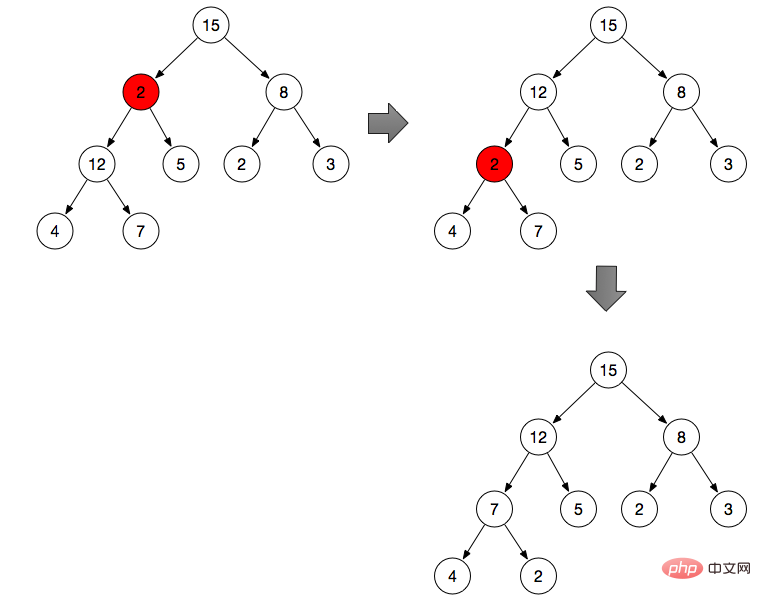
Wie oben gezeigt:
Verzweigungsknoten 2 anpassen (Verzweigungsknoten 2 erfüllt die Eigenschaften nicht des maximalen Heaps)
Standardmäßig ist der Verzweigungsknoten der Maximalwert
Vergleiche 2 mit links und rechte Zweige, von 2, 12, Finden Sie den Maximalwert in 5 und tauschen Sie dann die Position mit 2 aus
Erhalten Sie gemäß den oben genannten binären Heap-Eigenschaften den linken Knoten bzw. rechter Knoten von Zweigknoten 2
Vergleichen Sie drei Knoten und erhalten Sie das tiefgestellte Maximum des Maximalwerts
Wenn der Knoten selbst ist den Maximalwert, stoppen Sie den Vorgang
Tauschen Sie den Maximalknoten mit dem übergeordneten Knoten aus
Wiederholen Sie den Vorgang von Schritt 2, finden den Maximalwert aus 2, 4 und 7 und tausche ihn gegen 2 aus
Rekursion
maxHeapify(i) {
let max = i;
if(i >= this.size){
return;
}
// 当前序号的左节点
const l = i * 2 + 1;
// 当前需要的右节点
const r = i * 2 + 2;
// 求当前节点与其左右节点三者中的最大值
if(l this.data[max]){
max = l;
}
if(r this.data[max]){
max = r;
}
// 最终max节点是其本身,则已经满足最大堆性质,停止操作
if(max === i) {
return;
}
// 父节点与最大值节点做交换
const t = this.data[i];
this.data[i] = this.data[max];
this.data[max] = t;
// 递归向下继续执行
return this.maxHeapify(max);
}
Rekonstruktion des Heaps
Wir können sehen, dass der gerade initialisierte Heap durch ein Array dargestellt wird. Zu diesem Zeitpunkt erfüllt er möglicherweise nicht die Eigenschaften eines maximalen Heaps oder eines minimalen Heaps. Zu diesem Zeitpunkt müssen wir möglicherweise den gesamten Heap erstellen was wir wollen.
Wir haben die Max-Heapify-Operation oben durchgeführt und Max-Heapify passt nur einen bestimmten Zweigknoten an. Um den gesamten Heap in einen Maximum-Heap zu verwandeln, müssen Sie eine Max-Heapify-Operation auf allen Zweigknoten durchführen In der folgenden Abbildung müssen wir nacheinander Max-Hepify-Operationen für die vier Zweigknoten 12, 3, 2 und 15 ausführen.
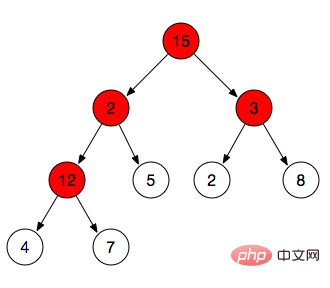
Spezifische Schritte :
Alle Zweigknoten finden: Die oben genannten Eigenschaften des Heaps erwähnen, dass die Seriennummer des Blattknotens>=Math.floor(n/2) ist, also kleiner als die Seriennummer von Math.floor(n/2) Dies sind alles Knoten, die wir anpassen müssen.
Das in der Mitte gezeigte Array ist beispielsweise [15,2,3,12,5,2,8,4,7] => (9/2 )=4 => Diejenigen mit einem Index kleiner als 4 sind 15, 2, 3 und 12 (Knoten, die angepasst werden müssen), während 5, 2, 8, 4 und 7 Blattknoten sind.
MaxHeapify-Vorgang auf allen gefundenen Knoten ausführen
rebuildHeap(){
// 叶子节点
const L = Math.floor(this.size / 2);
for(let i = L - 1; i>=0; i--){
this,maxHeapify(i);
}
}
Maximale Heap-Sortierung
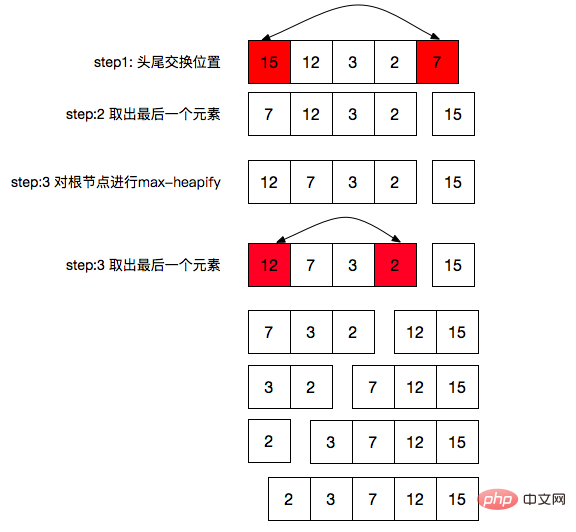
Die Sortierung des größten Haufens, wie in der Abbildung oben gezeigt:
Kopf- und Schwanzposition tauschen
-
Ändern Sie das letzte Element aus dem Heap, was der Größe 1 des Heaps entspricht
, und führen Sie dann eine Max-Heapify-Operation für das aus Heap-Wurzelknoten
Wiederholen In den obigen drei Schritten wissen wir, dass size=0 ist (wir haben diese Randbedingung bereits in der Max-Heapify-Funktion erfüllt)
sort() {
for(let i = this.size - 1; i > 0; i--){
swap(this.data, 0, i);
this.size--;
this.maxHeapify(0);
}
}
Einfügen und Löschen
Das Einfügen und Löschen dieser Löschung ist relativ einfach, nämlich das Einfügen und Löschen eines Arrays
Bis zum Ende einfügen
Heap-Länge + 1
Bestimmen Sie, ob es sich nach dem Einfügen noch um einen maximalen Heap handelt
Wenn nicht, rekonstruieren Sie den Heap
insert(key) {
this.data[this.size] = key;
this.size++
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
Ein Element im Array löschen
Heap-Länge -1
Bestimmen Sie, ob es sich um einen Heap handelt
Wenn nicht, refaktorieren Sie den Heap
delete(index) {
if (index >= this.size) {
return;
}
this.data.splice(index, 1);
this.size--;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
Komplettcode
/**
* 最大堆
*/
function left(i) {
return i * 2 + 1;
}
function right(i) {
return i * 2 + 2;
}
function swap(A, i, j) {
const t = A[i];
A[i] = A[j];
A[j] = t;
}
class Heap {
constructor(arr) {
this.data = [...arr];
this.size = this.data.length;
}
/**
* 重构堆
*/
rebuildHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i--) {
this.maxHeapify(i);
}
}
isHeap() {
const L = Math.floor(this.size / 2);
for (let i = L - 1; i >= 0; i++) {
const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;
const max = Math.max(this.data[i], l, r);
if (max !== this.data[i]) {
return false;
}
return true;
}
}
sort() {
for (let i = this.size - 1; i > 0; i--) {
swap(this.data, 0, i);
this.size--;
this.maxHeapify(0);
}
}
insert(key) {
this.data[this.size++] = key;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
delete(index) {
if (index >= this.size) {
return;
}
this.data.splice(index, 1);
this.size--;
if (this.isHeap()) {
return;
}
this.rebuildHeap();
}
/**
* 堆的其他地方都满足性质
* 唯独跟节点,重构堆性质
* @param {*} i
*/
maxHeapify(i) {
let max = i;
if (i >= this.size) {
return;
}
// 求左右节点中较大的序号
const l = left(i);
const r = right(i);
if (l this.data[max]) {
max = l;
}
if (r this.data[max]) {
max = r;
}
// 如果当前节点最大,已经是最大堆
if (max === i) {
return;
}
swap(this.data, i, max);
// 递归向下继续执行
return this.maxHeapify(max);
}
}
module.exports = Heap;
Zusammenfassung
Heap ist hier, Heap Es ist in einem Binärbaum relativ einfach und wird häufig zum Sortieren und für Prioritätswarteschlangen verwendet. Der Kern des Heaps ist die Max-Heapify-Operation und die drei Eigenschaften des Heaps.
Das obige ist der detaillierte Inhalt vonEinführung in Binärbäume (Binary Heaps) in JavaScript (Codebeispiele). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse