Heim >Backend-Entwicklung >Python-Tutorial >Einführung in das Wissen über die Komplexität sequentieller Listenalgorithmen in Python
Einführung in das Wissen über die Komplexität sequentieller Listenalgorithmen in Python
- 不言nach vorne
- 2018-10-29 17:21:533193Durchsuche
Dieser Artikel vermittelt Ihnen Wissen über die Komplexität sequentieller Tabellenalgorithmen in Python. Ich hoffe, dass er für Freunde hilfreich ist.
1. Einführung in die Algorithmuskomplexität
Für die Zeit- und Raumeigenschaften des Algorithmus ist seine Größe und sein Trend das Wichtigste, also die Funktion, mit der er gemessen werden soll Komplexität Der konstante Faktor kann ignoriert werden
Die Big-O-Notation ist normalerweise die asymptotische Zeitkomplexität eines bestimmten Algorithmus. Die Komplexität häufig verwendeter asymptotischer Komplexitätsfunktionen wird wie folgt verglichen:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
Ein Beispiel für die Einführung von Zeitkomplexität. Bitte vergleichen Sie die beiden Codebeispiele, um die Berechnungsergebnisse zu sehen
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a+b+c ==1000 and a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")

import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")
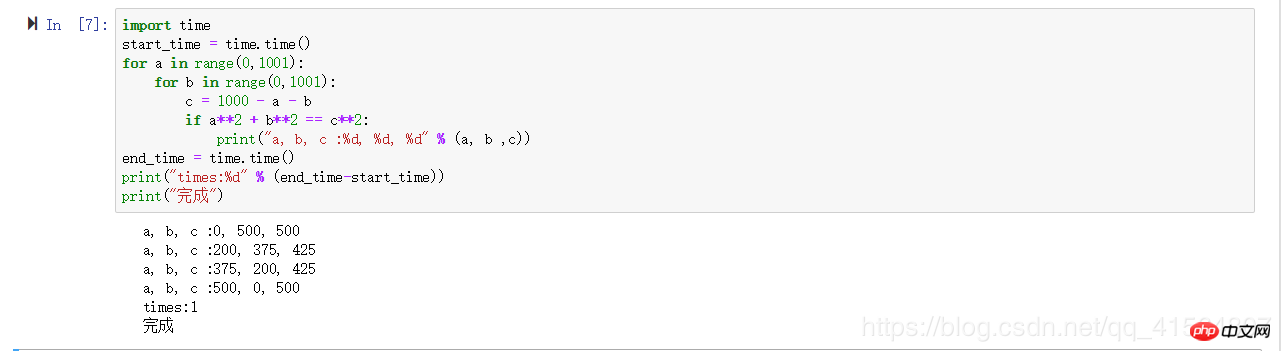
So berechnen Sie die Zeitkomplexität:
# 时间复杂度计算 # 1.基本步骤,基本操作,复杂度是O(1) # 2.顺序结构,按加法计算 # 3.循环,按照乘法 # 4.分支结构采用其中最大值 # 5.计算复杂度,只看最高次项,例如n^2+2的复杂度是O(n^2)
2. Zeitliche Komplexität von sequentiellen Listen
Test der zeitlichen Komplexität von Listen
# 测试
from timeit import Timer
def test1():
list1 = []
for i in range(10000):
list1.append(i)
def test2():
list2 = []
for i in range(10000):
# list2 += [i] # +=本身有优化,所以不完全等于list = list + [i]
list2 = list2 + [i]
def test3():
list3 = [i for i in range(10000)]
def test4():
list4 = list(range(10000))
def test5():
list5 = []
for i in range(10000):
list5.extend([i])
timer1 = Timer("test1()","from __main__ import test1")
print("append:",timer1.timeit(1000))
timer2 = Timer("test2()","from __main__ import test2")
print("+:",timer2.timeit(1000))
timer3 = Timer("test3()","from __main__ import test3")
print("[i for i in range]:",timer3.timeit(1000))
timer4 = Timer("test4()","from __main__ import test4")
print("list(range):",timer4.timeit(1000))
timer5 = Timer("test5()","from __main__ import test5")
print("extend:",timer5.timeit(1000))
Ergebnisse ausgeben

Komplexität der Methoden in der Liste:
# 列表方法中复杂度 # index O(1) # append 0(1) # pop O(1) 无参数表示是从尾部向外取数 # pop(i) O(n) 从指定位置取,也就是考虑其最复杂的状况是从头开始取,n为列表的长度 # del O(n) 是一个个删除 # iteration O(n) # contain O(n) 其实就是in,也就是说需要遍历一遍 # get slice[x:y] O(K) 取切片,即K为Y-X # del slice O(n) 删除切片 # set slice O(n) 设置切片 # reverse O(n) 逆置 # concatenate O(k) 将两个列表加到一起,K为第二个列表的长度 # sort O(nlogn) 排序,和排序算法有关 # multiply O(nk) K为列表的长度
Komplexität der Methoden im Wörterbuch (ergänzend)
# 字典中的复杂度 # copy O(n) # get item O(1) # set item O(1) 设置 # delete item O(1) # contains(in) O(1) 字典不用遍历,所以可以一次找到 # iteration O(n)
3. Datenstruktur der Sequenztabelle
Die vollständigen Informationen einer Sequenztabelle bestehen aus zwei Teilen, einem Teil ist die Menge der Elemente in der Tabelle und der andere Teil Ein Teil besteht darin, einen korrekten Betrieb zu erreichen. Zu den Informationen, die aufgezeichnet werden müssen, gehören hauptsächlich die Kapazität des Elementspeicherbereichs und die Anzahl der Elemente in der aktuellen Tabelle.
Kombination aus Header- und Datenbereich: Integrierte Struktur: Header-Informationen (Aufnahmekapazität und Anzahl vorhandener Elemente) und Datenbereich zur kontinuierlichen Speicherung
-
Getrennte Struktur: Header-Informationen und Datenbereich werden nicht kontinuierlich gespeichert, und einige Informationen werden zum Speichern von Adresseinheiten verwendet, um auf den tatsächlichen Datenbereich zu verweisen
Die Unterschiede und Vor- und Nachteile zwischen den beiden:
# 1.一体式结构:数据必须整体迁移 # 2.分离式结构:在数据动态的过错中有优势rrree
4. Strategien für die Erweiterung des variablen Speicherplatzes in Python
1 Beim Erstellen einer leeren Tabelle (oder (eine sehr kleine Tabelle) weist das System einen Speicherbereich zu, der 8 Elemente aufnehmen kann
2. Wenn der Elementspeicherbereich beim Ausführen von Einfügevorgängen (Einfügen, Anhängen) voll ist, ersetzen Sie ihn durch einen Speicherbereich von 4 Verdoppeln Sie den Speicherbereich
3. Wenn die Tabelle bereits sehr groß ist (der Schwellenwert liegt bei 50000), ändern Sie die Richtlinie und übernehmen Sie die Methode zur Verdoppelung der Größe. Um zu viel freien Speicherplatz zu vermeiden.
Das obige ist der detaillierte Inhalt vonEinführung in das Wissen über die Komplexität sequentieller Listenalgorithmen in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

