JavaScript berechnet die Entfernung zwischen zwei Orten anhand des Breiten- und Längengrads

Wie berechnet man mit JavaScript die Entfernung zwischen zwei Orten? Ich glaube, dass es viele Möglichkeiten gibt, dies zu erreichen. Der folgende Artikel führt Sie in JavaScript ein, um die Entfernung zwischen zwei Orten anhand von Längen- und Breitengraden zu berechnen.

Kürzlich habe ich aus beruflichen Gründen online nach Methoden gesucht, um die Entfernung zwischen zwei Orten basierend auf Längen- und Breitengrad zu berechnen. Dabei habe ich festgestellt, dass es sich entweder um eine geometrische Methode, das Zeichnen eines Bildes oder das Erstellen eines Bildes handelt Reihe von Hilfszeilen und dann die Argumentation beweisen oder sie einfach anwenden, ohne etwas zu sagen. In diesem Artikel wird eine leicht verständliche Möglichkeit vorgestellt, diesen Abstand zu ermitteln.

Idee

Der Einfachheit halber betrachten wir sie zur Berechnung als Kugel.
Der kürzeste Abstand zwischen zwei Orten auf einer Kugel ist die Länge des kleinen Bogens eines Großkreises, der durch zwei Punkte verläuft.

Die Idee ist wie folgt:

Bogenlänge ← Sehnenlänge (Abstand zwischen zwei Punkten) ← Zweipunktkoordinaten (rechteckige Koordinaten) ← Breiten- und Längengrad

Berechnen

1. Koordinatenumrechnung

Angenommen:

Der Radius der Erde ist $R$

Die Linie, die den Mittelpunkt der Erde mit verbindet E 0° N 0° ist die x-Achse

Die Linie, die den Mittelpunkt der Erde mit E 90° N 0° verbindet, ist die y-Achse

Die Linie, die den Mittelpunkt der Erde verbindet Erde zu E 0° N 90° ist die z-Achse

Es gibt einen Punkt $A auf der Erdoberfläche $, der Längengrad ist $e$, der Breitengrad ist $n$ und die Einheit ist Bogenmaß

, dann können die Koordinaten von $A$ ausgedrückt werden als:

$$ x = R cdot cos(n) cdot cos(e)\ y = R cdot cos(n) cdot sin(e)\ z = R cdot sin(n) $$

Code

const R = 6371
const {cos, sin, PI} = Math

let getPoint = (e, n) => {
    //首先将角度转为弧度
    e *= PI/180
    n *= PI/180
    reutrn {
        x: R*cos(n)*cos(e),
        y: R*cos(n)*sin(e),
        z: R*sin(n)
    }
}

2. Berechnen Sie den Abstand zwischen zwei Punkten anhand von Koordinaten

Das ist zu einfach, überspringen Sie

3. Ermitteln Sie die Bogenlänge anhand der Sehnenlänge

Sie können ein Bild zeichnen, um das Verständnis zu erleichtern:

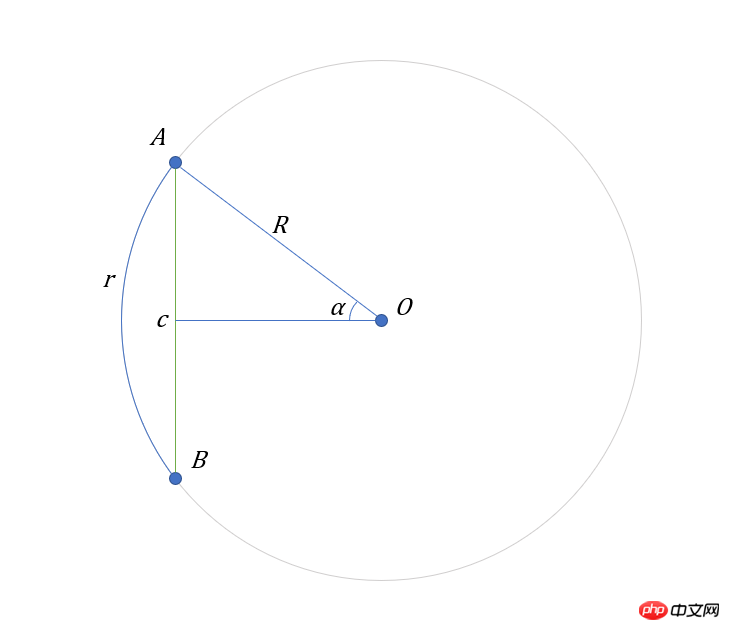
Jetzt die Die Sehnenlänge $c$ ist bekannt, der Radius $R$ erfordert die Länge des Bogens $r$
Das ist sehr einfach, ermitteln Sie einfach zuerst die Größe von $∠alpha$:

$$ alpha = arcsin(c/2/R)\ r = 2alpha cdot R $$

Code

const {asin} = Math
const R = 6371

r = asin(c/2/R)*2*R

Endgültiger Code

/**
 * 获取两经纬度之间的距离
 * @param {number} e1 点1的东经, 单位:角度, 如果是西经则为负
 * @param {number} n1 点1的北纬, 单位:角度, 如果是南纬则为负
 * @param {number} e2
 * @param {number} n2
 */
function getDistance(e1, n1, e2, n2){
    const R = 6371
    const { sin, cos, asin, PI, hypot } = Math
    
    /** 根据经纬度获取点的坐标 */
    let getPoint = (e, n) => {
        e *= PI/180
        n *= PI/180
        //这里 R* 被去掉, 相当于先求单位圆上两点的距, 最后会再将这个距离放大 R 倍
        return {x: cos(n)*cos(e), y: cos(n)*sin(e), z: sin(n)}
    }
    
    let a = getPoint(e1, n1)
    let b = getPoint(e2, n2)
    let c = hypot(a.x - b.x, a.y - b.y, a.z - b.z)
    let r = asin(c/2)*2*R
    return r
}

Verwandte Empfehlungen:

Berechnen Sie die Entfernung zwischen zwei Orten basierend auf Längen- und Breitengrad

PHP berechnet die Entfernung basierend auf dem Längen- und Breitengrad zwischen zwei Punkten, PHP berechnet den Längen- und Breitengrad von zwei Punkten

Das obige ist der detaillierte Inhalt vonJavaScript berechnet die Entfernung zwischen zwei Orten anhand des Breiten- und Längengrads. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!