Heim >Web-Frontend >js-Tutorial >Ausführliche Fallerklärung: Einführung in die dynamische Programmierung (am Beispiel von Treppen)
Ausführliche Fallerklärung: Einführung in die dynamische Programmierung (am Beispiel von Treppen)
- php是最好的语言Original
- 2018-08-09 16:33:274047Durchsuche
Konzept
Dynamische Programmierung ist ein Zweig des Operations Research und eine mathematische Methode zur Optimierung des Entscheidungsprozesses.
Dynamische Programmieralgorithmen basieren normalerweise auf einer Rekursionsformel und einem oder mehreren Anfangszuständen. Die Lösung des aktuellen Teilproblems wird aus der Lösung des vorherigen Teilproblems abgeleitet.
Grundidee
Um ein gegebenes Problem zu lösen, müssen wir seine verschiedenen Teile lösen (d. h. Unterprobleme lösen) und dann die Lösungen der Unterprobleme kombinieren um eine Lösung für das ursprüngliche Problem zu finden.
Normalerweise sind viele Teilprobleme sehr ähnlich, daher versucht die dynamische Programmierung, jedes Teilproblem nur einmal zu lösen , um den Rechenaufwand zu reduzieren.
Sobald die Lösung für ein bestimmtes Teilproblem berechnet wurde, wird sie gespeichert und gespeichert, sodass die Tabelle direkt nachgeschlagen werden kann, wenn die Lösung für dasselbe Teilproblem das nächste Mal benötigt wird .
Dieser Ansatz ist besonders nützlich, wenn die Anzahl der wiederholten Teilprobleme exponentiell mit der Größe der Eingabe wächst.
Dynamische Programmierung hat drei Kernelemente:
1. Optimale Unterstruktur
3. Zustandsübergangsgleichung
Ein weiteres Beispiel: Machen Sie jedes Mal zwei Schritte, also insgesamt fünf Schritte. Dies ist eine andere Art des Gehens.
Aber es ist zu mühsam, dies einzeln zu tun. Wir können einfach darüber nachdenken, wie wir den letzten Schritt machen, wie unten gezeigt
Wie wir zum zehnten gelangen Treppe wie folgt = Gehe zur achten Treppe + Gehe zur neunten Treppe 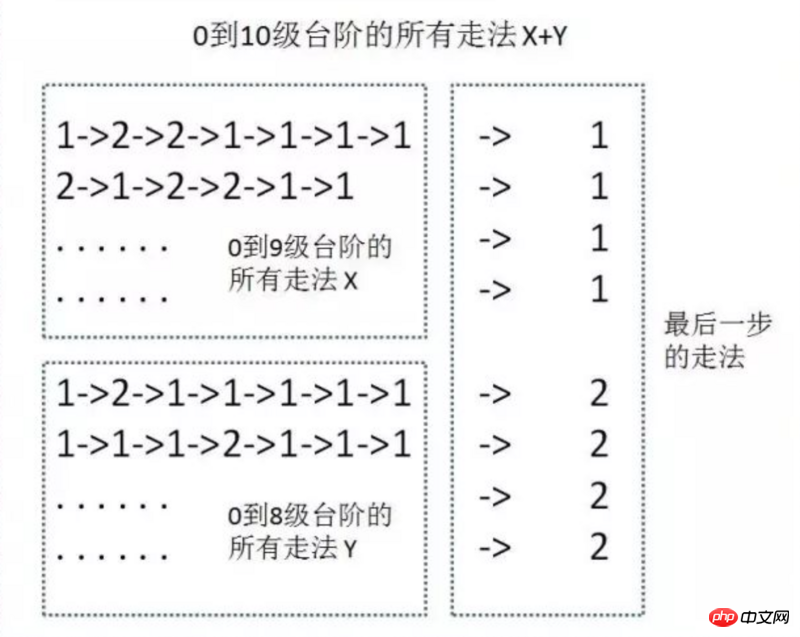 Wir verwenden f(n), um den Weg zur n-ten Treppe darzustellen, also haben wir f(10) = f(9) + f( 8)
Wir verwenden f(n), um den Weg zur n-ten Treppe darzustellen, also haben wir f(10) = f(9) + f( 8)
Auf diese Weise Wir erhalten eine
rekursive Formel
f(n) = f(n-1) + f(n-2);
und zwei weitere Ausgangszustand :
f(1) = 1;
f(2) = 2;
Dies gibt uns die A-Lösung
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return getWays(n-1) + getWays(n-2);
}Die zeitliche Komplexität dieser Methode beträgt O(2^n)
Sie können sehen, dass es sich um einen Binärbaum handelt. Die Anzahl der Knoten gibt an, wie oft unsere rekursive Gleichung berechnet werden muss. 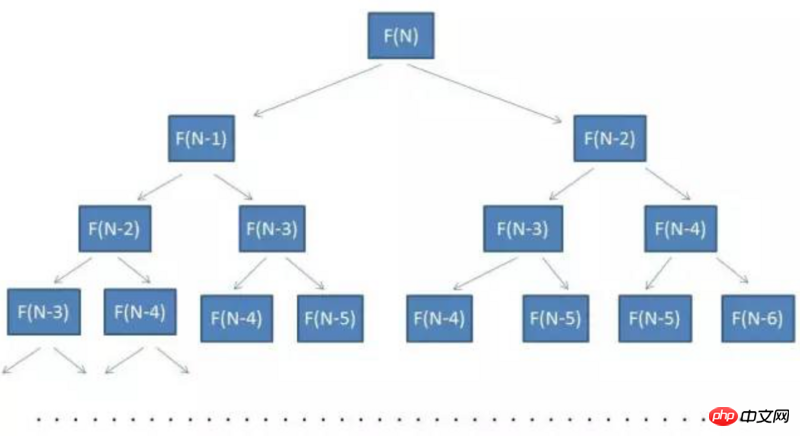 Die Höhe der Zahl beträgt N und die Anzahl der Knoten beträgt ungefähr 2^n
Die Höhe der Zahl beträgt N und die Anzahl der Knoten beträgt ungefähr 2^n
Aber kann diese Methode optimiert werden?
Wir werden feststellen, dass einige Werte wiederholt berechnet werden, wie unten gezeigt
Die gleiche Farbe stellt die wiederholten Teile dar. Können wir diese wiederholt berechneten Werte
aufzeichnen
? 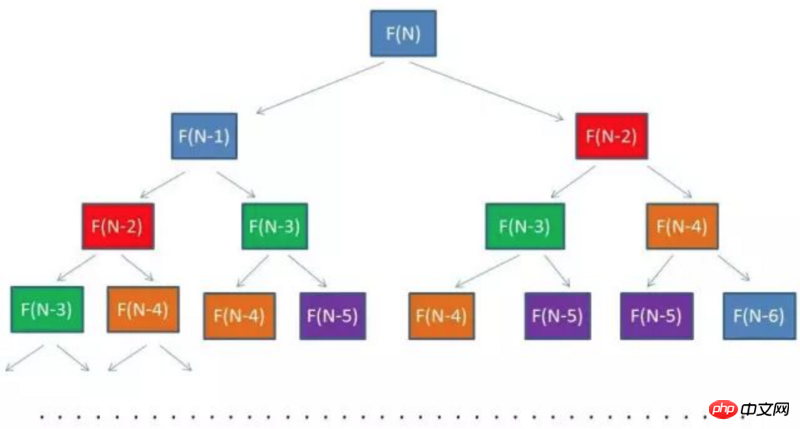 Eine solche Optimierung hat eine zweite MethodeMethode 2: Memo-Algorithmus
Eine solche Optimierung hat eine zweite MethodeMethode 2: Memo-Algorithmus
const map = new Map();
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
if (map.has(n)) {
return map.get(n);
}
const value = getWays(n-1) + getWays(n-2);
map.set(n, value);
return value;
}Weil n-2 Schlüssel-Wert-Paare schließlich in der Karte gespeichert werden, Die Raumkomplexität ist also O(n)und die Zeitkomplexität ist auch
O(n) Das ist die optimale Lösung. ?
Kehren wir zur ursprünglichen Idee zurück. Wir gingen davon aus, dass die vorherige Treppe begangen wurde und betrachteten nur die letzte Stufe, sodass wir zu dem Schluss kamen, dass f(n) = f(n-1) + f (n-2), dies ist eine Top-Down-LösungIm Allgemeinen sollte man nach normaler Denkweise Schritt für Schritt vorgehen. Es sollte von unten nach oben gelöst werden, um mehr mit der Denkweise normaler Menschen übereinzustimmen . Mal sehen, ob es funktioniert
Dies ist die Anzahl der Stufen für eine und zwei Stufen am Anfang, das ist der
 Dies ist eine Iteration, um drei Stufen zu erhalten. f(3) hängt nur von f(1) und f(2) ab
Dies ist eine Iteration, um drei Stufen zu erhalten. f(3) hängt nur von f(1) und f(2) ab
Fahren Sie mit dem nächsten Schritt fort
Wir stellen fest, dass für jede Iteration nur die ersten beiden Iterationen erforderlich sind. Es besteht keine Notwendigkeit, die Daten von zu speichern alle Unterzustände wie ein Memo 
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
// a保存倒数第二个子状态数据,b保存倒数第一个子状态数据, temp 保存当前状态的数据
let a = 1, b = 2;
let temp = a + b;
for (let i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}Hier können wir uns die aktuelle Zeitkomplexität, Zeitkomplexität und Raumkomplexität ansehenDie aktuelle Zeitkomplexität ist immer nochO(n)
, aber die räumliche Komplexität ist auf
O(1) reduziertDies ist das ideale ErgebnisZusammenfassung
Wenn die Änderungsdimensionen zwei, drei oder sogar mehr werden, wird es noch komplizierter. Komplex, der Rucksack Das Problem ist ein typisches mehrdimensionales Problem. Wenn Sie interessiert sind, können Sie online „Neun Vorträge über Rucksäcke“ lesen
Verwandte Empfehlungen:
Detaillierte Erläuterung der Verwendung der dynamischen JS-Programmierung
Analyse dynamischer Programmierbeispiele für fortgeschrittene JavaScript-Algorithmen
Das obige ist der detaillierte Inhalt vonAusführliche Fallerklärung: Einführung in die dynamische Programmierung (am Beispiel von Treppen). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

