Heim > Artikel > Backend-Entwicklung > Beispiel für die Implementierung des Deming-Regressionsalgorithmus mit TensorFlow
Beispiel für die Implementierung des Deming-Regressionsalgorithmus mit TensorFlow
- 不言Original
- 2018-05-02 13:55:082206Durchsuche
Dieser Artikel stellt hauptsächlich Beispiele für die Verwendung von TensorFlow zur Implementierung des Deming-Regressionsalgorithmus vor. Er hat einen bestimmten Referenzwert. Jetzt können Freunde in Not darauf zurückgreifen.
Wenn die kleinste Quadrate lineare Regression ist Der Algorithmus minimiert den vertikalen Abstand zur Regressionslinie (d. h. parallel zur y-Achsenrichtung), dann minimiert die Deming-Regression den Gesamtabstand zur Regressionslinie (d. h. senkrecht zur Regressionslinie). Es minimiert den Fehler in beiden Richtungen des X-Werts und des Y-Werts. Die spezifische Vergleichstabelle sieht wie folgt aus.
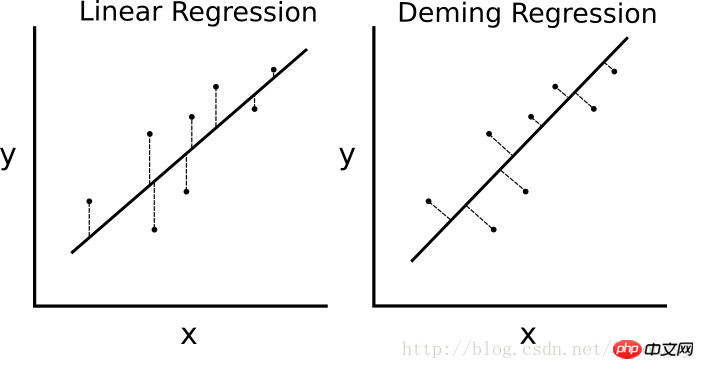
Der Unterschied zwischen dem linearen Regressionsalgorithmus und dem Deming-Regressionsalgorithmus. Die lineare Regression auf der linken Seite minimiert den vertikalen Abstand zur Regressionsgeraden; die Deming-Regression auf der rechten Seite minimiert den Gesamtabstand zur Regressionsgeraden.
Die Verlustfunktion des linearen Regressionsalgorithmus minimiert den vertikalen Abstand; hier ist es notwendig, den Gesamtabstand zu minimieren. Angesichts der Steigung und des Achsenabschnitts einer geraden Linie gibt es eine bekannte geometrische Formel zur Lösung des vertikalen Abstands von einem Punkt zur geraden Linie. Setzen Sie die geometrische Formel ein und lassen Sie TensorFlow den Abstand minimieren.
Die Verlustfunktion ist eine geometrische Formel, die aus einem Zähler und einem Nenner besteht. Bei einer gegebenen geraden Linie y=mx+b und einem Punkt (x0, y0) lautet die Formel zum Ermitteln des Abstands zwischen den beiden:
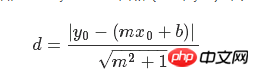
# 戴明回归
#----------------------------------
#
# This function shows how to use TensorFlow to
# solve linear Deming regression.
# y = Ax + b
#
# We will use the iris data, specifically:
# y = Sepal Length
# x = Petal Width
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
# Create graph
sess = tf.Session()
# Load the data
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
# Declare batch size
batch_size = 50
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)
# Declare Demming loss function
demming_numerator = tf.abs(tf.subtract(y_target, tf.add(tf.matmul(x_data, A), b)))
demming_denominator = tf.sqrt(tf.add(tf.square(A),1))
loss = tf.reduce_mean(tf.truep(demming_numerator, demming_denominator))
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.1)
train_step = my_opt.minimize(loss)
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
# Training loop
loss_vec = []
for i in range(250):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
if (i+1)%50==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# Get best fit line
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
# Plot the result
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title('L2 Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('L2 Loss')
plt.show()
Ergebnisse:
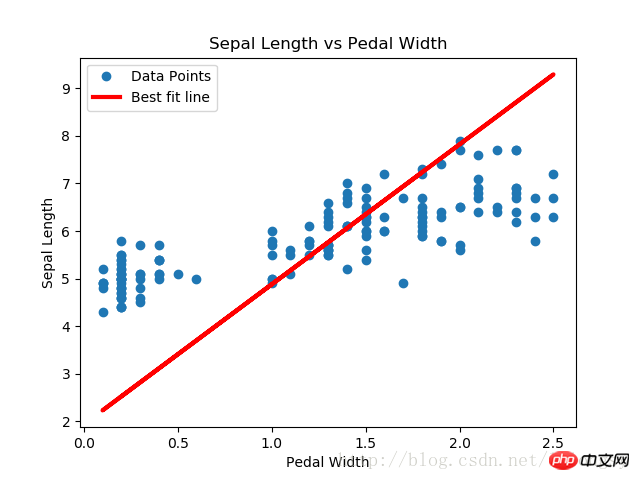
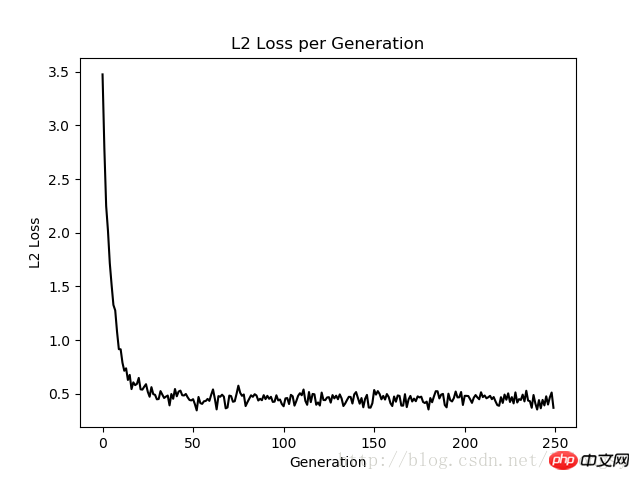
Die mit dem Deming-Regressionsalgorithmus und der linearen Regression erhaltenen Ergebnisse Algorithmus in diesem Artikel Im Grunde das Gleiche. Der Hauptunterschied zwischen den beiden ist die Messung der Verlustfunktion zwischen dem vorhergesagten Wert und dem Datenpunkt: Die Verlustfunktion des linearen Regressionsalgorithmus ist der vertikale Distanzverlust, während der Deming-Regressionsalgorithmus der vertikale Distanzverlust ist (Gesamtwert). x-Achse und y-Achse Distanzverlust).
Beachten Sie, dass der Implementierungstyp des Deming-Regressionsalgorithmus hier die Gesamtregression ist (gesamter Fehler der kleinsten Quadrate). Der allgemeine Regressionsalgorithmus geht davon aus, dass die Fehler in den x- und y-Werten ähnlich sind. Wir können auch unterschiedliche Fehler verwenden, um die Abstandsberechnung der x-Achse und der y-Achse nach unterschiedlichen Konzepten zu erweitern.
Verwandte Empfehlungen:
Beispielcode für die Implementierung von Multi-Class-Support-Vektor-Maschinen mit TensorFlow
TensorFlow implementiert nichtlineare Support-Vektor-Maschinen-Methode
Das obige ist der detaillierte Inhalt vonBeispiel für die Implementierung des Deming-Regressionsalgorithmus mit TensorFlow. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

