Heim >Backend-Entwicklung >Python-Tutorial >Wie TensorFlow Zufallstraining und Batch-Training implementiert
Wie TensorFlow Zufallstraining und Batch-Training implementiert
- 不言Original
- 2018-04-28 10:00:452744Durchsuche
In diesem Artikel wird hauptsächlich die Methode von TensorFlow zur Implementierung von Zufallstraining und Batch-Training vorgestellt. Jetzt teile ich sie mit Ihnen und gebe sie als Referenz. Kommen Sie und werfen Sie gemeinsam einen Blick darauf
TensorFlow aktualisiert Modellvariablen. Es kann jeweils einen Datenpunkt oder große Datenmengen gleichzeitig bearbeiten. Die Arbeit an einem einzelnen Trainingsbeispiel kann zu einem „skurrilen“ Lernprozess führen, aber das Training mit großen Batches kann rechenintensiv sein. Welche Trainingsart gewählt wird, ist für die Konvergenz des maschinellen Lernalgorithmus von entscheidender Bedeutung.
Damit TensorFlow variable Gradienten berechnen kann, damit die Rückausbreitung funktioniert, müssen wir den Verlust an einer oder mehreren Proben messen.
Beim Zufallstraining werden zufällig Trainingsdaten und Zieldatenpaare abgetastet, um das Training abzuschließen. Eine weitere Möglichkeit besteht darin, den Verlust für die Gradientenberechnung in einem großen Batch-Training zu mitteln. Die Batch-Trainingsgröße kann auf einmal auf den gesamten Datensatz erweitert werden. Hier zeigen wir, wie man das vorherige Beispiel eines Regressionsalgorithmus erweitert – mithilfe von Zufallstraining und Batch-Training.
Batch-Training und Zufallstraining unterscheiden sich in ihren Optimierungsmethoden und ihrer Konvergenz.
# 随机训练和批量训练
#----------------------------------
#
# This python function illustrates two different training methods:
# batch and stochastic training. For each model, we will use
# a regression model that predicts one model variable.
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
# 随机训练:
# Create graph
sess = tf.Session()
# 声明数据
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[1], dtype=tf.float32)
y_target = tf.placeholder(shape=[1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1]))
# 增加操作到图
my_output = tf.multiply(x_data, A)
# 增加L2损失函数
loss = tf.square(my_output - y_target)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_stochastic = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100)
rand_x = [x_vals[rand_index]]
rand_y = [y_vals[rand_index]]
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_stochastic.append(temp_loss)
# 批量训练:
# 重置计算图
ops.reset_default_graph()
sess = tf.Session()
# 声明批量大小
# 批量大小是指通过计算图一次传入多少训练数据
batch_size = 20
# 声明模型的数据、占位符
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1,1]))
# 增加矩阵乘法操作(矩阵乘法不满足交换律)
my_output = tf.matmul(x_data, A)
# 增加损失函数
# 批量训练时损失函数是每个数据点L2损失的平均值
loss = tf.reduce_mean(tf.square(my_output - y_target))
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_batch = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100, size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_batch.append(temp_loss)
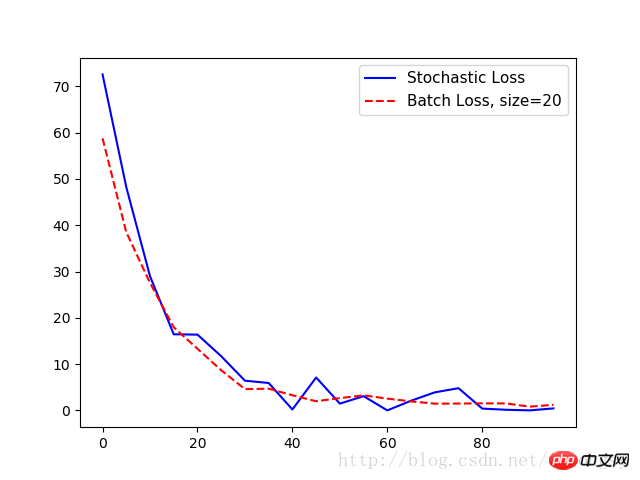
plt.plot(range(0, 100, 5), loss_stochastic, 'b-', label='Stochastic Loss')
plt.plot(range(0, 100, 5), loss_batch, 'r--', label='Batch Loss, size=20')
plt.legend(loc='upper right', prop={'size': 11})
plt.show()
Ausgabe:
Schritt Nr. 5 A = [ 1,47604525]
Verlust = [ 72,55678558]
Schritt #10 A = [ 3,01128507]
Verlust = [ 48,22986221]
Schritt #15 A = [ 4,27042341]
Verlust = [ 28,97912598]
Schritt #20 A = [ 5,2984333]
Verlust s = [16.44779968]
Schritt #25 A = [6.17473984]
Verlust = [16.373312]
Schritt #30 A = [6.89866304]
Verlust = [11.71054649] = [[[ 7.39849901]
Verlust = [ 6,42773056]
Schritt #40 A = [ 7,84618378]
Verlust = [ 5,92940331]
Schritt #45 A = [ 8,15709782]
Verlust = [ 0,2 142024]
Schritt # 50 A = [ 8,54818344]
Verlust = [ 7,11651039]
Schritt #55 A = [ 8,82354641]
Verlust = [ 1,47823763]
Schritt #60 A = [ 9,07896614]
= [ 3,08244276]
SCHRITT #65 A = [9,24868107]
Verlust = [0,01143846]
SCHRITT #70 A = [9,36772251]
VERLUST = [2,10078788]
Schritt #75 A = [9,49171 734 ]
Verlust = [3.90913701]
Schritt #80 a = [9.6622715]
Verlust = [4.80727625]
Schritt #85 a = [9.73786926]
Verlust = [0. 39915398] Schritt #90 A = [9,81853104]
Verlust = [0,14876099]
Schritt #95 A = [9,90371323]
VERLUST = [0,01657014]
SCHRITT #100 A = [9,86669159159159 Verlust = [ 0,444787]
Schritt Nr. 5 A = [[ 2,34371352]]
Verlust = 58,766
Schritt Nr. 10 A = [[ 3,74766445]]
Verlust = 38,4875
Schritt Nr. 15 A = [[ 4,88928795]]
Verlust = 27,5632
Schritt #20 A = [[ 5,82038736]]
Verlust = 17,9523
Schritt #25 A = [[ 6,58999157]]
Verlust = 13.3245
Schritt #30 a = [[7.20851326]]
Verlust = 8,68099
Schritt #35 a = [[7.71694899]]
Verlust = 4,60659
Schritt #40 A = [8.12967111111111111111111111111111111111111111111111111111111111111111111111111112). ]]
Verlust = 4,70107
Schritt #45 A = [[ 8,47107315]]
Verlust = 3,28318
Schritt #50 A = [[ 8,74283409]]
Verlust = 1,99057
Schritt #55 A = [[ 8,98811722]]
Verlust = 2,66906
Schritt #60 A = [[ 9,18062305]]
Verlust = 3,26207
Schritt #65 A = [[ 9,31655025]]
Verlust = 2,55459
Schritt Nr. 70 A = [[ 9,43130589]]
Verlust = 1,95839
Schritt Nr. 75 A = [[ 9,55670166]]
Verlust = 1,46504
Schritt Nr. 80 A = [ [9,6354847]]
Verlust = 1,49021
Schritt Nr. 85 A = [[9,73470974]]
Verlust = 1,53289
Schritt Nr. 90 A = [[9,77956581]]
Verlust = 1,52173
Schritt Nr. 95 A = [[ 9,83666706]]
Verlust = 0,819207
Schritt Nr. 100 A = [[ 9,85569191]]
Verlust = 1,2197
Verwandte Empfehlungen:
| 训练类型 | 优点 | 缺点 |
|---|---|---|
| 随机训练 | 脱离局部最小 | 一般需更多次迭代才收敛 |
| 批量训练 | 快速得到最小损失 | 耗费更多计算资源 |
Ein kurzer Vortrag über die Tensorflow1.0-Pooling-Schicht (Pooling) und die vollständig verbundene Schicht (dicht)
Eine kurze Diskussion zum Speichern, Wiederherstellen und Laden von Tensorflow-Modellen
Das obige ist der detaillierte Inhalt vonWie TensorFlow Zufallstraining und Batch-Training implementiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

