Heim >Backend-Entwicklung >Python-Tutorial >Python implementiert den klassischen LR-Algorithmus
Python implementiert den klassischen LR-Algorithmus
- 零到壹度Original
- 2018-04-19 16:55:445743Durchsuche
Das Beispiel in diesem Artikel beschreibt die Implementierung des klassischen LR-Algorithmus in Python. Teilen Sie es wie folgt als Referenz mit allen:
(1) Den Logistic Regression (LR)-Klassifikator verstehen
Obwohl der Name der logistischen Regression „Regression“ enthält, handelt es sich tatsächlich um eine Klassifizierungsmethode, die hauptsächlich für Zwei-Klassifizierungsprobleme verwendet wird. Sie verwendet die logistische Funktion (oder Sigmoid-Funktion) und die unabhängige Variable Der Wertebereich ist ( -INF, INF), der Wertebereich der unabhängigen Variablen ist (0,1) und die Funktionsform ist:

Da der Definitionsbereich der Sigmoidfunktion (-INF, +INF) ist, beträgt der Wertebereich (0 , 1). Daher eignet sich der grundlegendste LR-Klassifikator zur Klassifizierung von Zielen in zwei Kategorien (Klasse 0, Klasse 1). Die Sigmoid-Funktion hat eine sehr schöne „S“-Form, wie in der folgenden Abbildung dargestellt:

LR Klassifikator (Der Zweck des Logistic Regression Classifier besteht darin, ein 0/1-Klassifizierungsmodell aus den Trainingsdatenmerkmalen zu lernen. Dieses Modell verwendet die lineare Kombination von Beispielmerkmalen  als unabhängige Variable und verwendet die logistische Funktion, um die unabhängige Variable abzubilden zu (0,1). Daher besteht die Lösung des LR-Klassifikators darin, eine Reihe von Gewichten zu lösen Wenn ein konstanter Begriff sinnvoll ist oder nicht, ist es am besten, ihn beizubehalten. Ersetzen Sie ihn in die Logistikfunktion, um eine Vorhersagefunktion zu erstellen:
als unabhängige Variable und verwendet die logistische Funktion, um die unabhängige Variable abzubilden zu (0,1). Daher besteht die Lösung des LR-Klassifikators darin, eine Reihe von Gewichten zu lösen Wenn ein konstanter Begriff sinnvoll ist oder nicht, ist es am besten, ihn beizubehalten. Ersetzen Sie ihn in die Logistikfunktion, um eine Vorhersagefunktion zu erstellen: 


Wenn wir bestimmen möchten, zu welcher Klasse ein neues Feature gehört, einen Z-Wert gemäß der folgenden Formel ermitteln: 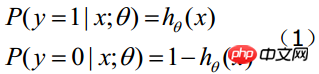
(x1,x2,...,xn sind die verschiedenen Merkmale bestimmter Beispieldaten, die Dimension ist n)
Dann finden Sie es heraus ---wenn es größer als 0,5 ist, ist es Klasse y=1, andernfalls gehört es zur Klasse y=0. (Hinweis: Es wird weiterhin davon ausgegangen, dass die statistischen Stichproben gleichmäßig verteilt sind, daher wird der Schwellenwert auf 0,5 festgelegt.) Wie erhält man diesen Gewichtssatz des LR-Klassifikators? Dies erfordert die Konzepte der Maximum-Likelihood-Schätzung MLE und Optimierungsalgorithmen. Der in der Mathematik am häufigsten verwendete Optimierungsalgorithmus ist der Gradientenaufstiegs-(Abstiegs-)Algorithmus.
Logistische Regression kann auch für die Klassifizierung mehrerer Klassen verwendet werden, die binäre Klassifizierung wird jedoch häufiger verwendet und ist einfacher zu erklären. Daher ist die in der Praxis am häufigsten verwendete Methode die binäre logistische Regression. Der LR-Klassifikator eignet sich für Datentypen: numerische und nominale Daten. Sein Vorteil besteht darin, dass der Berechnungsaufwand nicht hoch ist und er leicht zu verstehen und umzusetzen ist; sein Nachteil besteht darin, dass er leicht unteranpassungsfähig ist und die Klassifizierungsgenauigkeit möglicherweise nicht hoch ist.
(2) Mathematische Ableitung der logistischen Regression
1. Gradientenabstiegsmethode zur Lösung der logistischen Regression
Um den folgenden mathematischen Ableitungsprozess zu verstehen, sind zunächst mehr Ableitungslösungsformeln erforderlich. Sie können sich auf „Häufig verwendete grundlegende Elementarfunktionsableitungsformeln und Integralformeln“ beziehen.
Angenommen, es gibt n Beobachtungsproben und die Beobachtungswerte sind jeweils  Sei
Sei  die Wahrscheinlichkeit, unter bestimmten Bedingungen yi=1 zu erhalten. Die bedingte Wahrscheinlichkeit, unter den gleichen Bedingungen yi=0 zu erhalten, beträgt
die Wahrscheinlichkeit, unter bestimmten Bedingungen yi=1 zu erhalten. Die bedingte Wahrscheinlichkeit, unter den gleichen Bedingungen yi=0 zu erhalten, beträgt  . Daher ist die Wahrscheinlichkeit, einen Beobachtungswert zu erhalten,
. Daher ist die Wahrscheinlichkeit, einen Beobachtungswert zu erhalten,
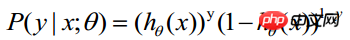 -----Diese Formel ist eigentlich eine umfassende Formel (1), um
-----Diese Formel ist eigentlich eine umfassende Formel (1), um
Da jede Beobachtung unabhängig ist, kann ihre gemeinsame Verteilung als Produkt jeder Randverteilung ausgedrückt werden:
(m stellt die Anzahl der statistischen Stichproben dar) >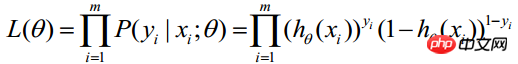 Die obige Formel wird als Wahrscheinlichkeitsfunktion von n Beobachtungen bezeichnet. Unser Ziel ist es, Parameterschätzungen zu finden, die den Wert dieser Wahrscheinlichkeitsfunktion maximieren. Daher besteht der Schlüssel zur Maximum-Likelihood-Schätzung darin, die Parameter
Die obige Formel wird als Wahrscheinlichkeitsfunktion von n Beobachtungen bezeichnet. Unser Ziel ist es, Parameterschätzungen zu finden, die den Wert dieser Wahrscheinlichkeitsfunktion maximieren. Daher besteht der Schlüssel zur Maximum-Likelihood-Schätzung darin, die Parameter
 Finden Sie den Logarithmus der obigen Funktion:
Finden Sie den Logarithmus der obigen Funktion:
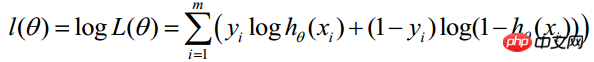
Die Maximum-Likelihood-Schätzung besteht darin, θ zu ermitteln, wenn die obige Formel den Maximalwert annimmt. Zur Lösung kann die Gradientenanstiegsmethode verwendet werden. Im Kurs von Andrew Ng wird J(θ) als die folgende Formel verwendet, das heißt: J(θ)=-(1/m)l(θ), und θ, wenn J(θ) sein Minimum erreicht, ist das erforderliche Optimum Parameter. Ermitteln Sie den Mindestwert mithilfe der Gradientenabstiegsmethode. Die Anfangswerte von θ können alle 1,0 sein, und der Aktualisierungsprozess ist:
(j stellt das j-te Attribut der Stichprobe dar, n insgesamt; a stellt das dar Schrittgröße – jede Bewegung. Der Betrag kann frei angegeben werden 🎜> Daher kann θ (Der Aktualisierungsprozess (kann alle Anfangswerte auf 1,0 setzen) geschrieben werden als:
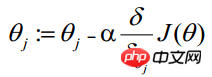
 (i stellt die i-te statistische Stichprobe dar, j stellt das j-te Attribut der Stichprobe dar; a stellt die Schrittgröße dar)
(i stellt die i-te statistische Stichprobe dar, j stellt das j-te Attribut der Stichprobe dar; a stellt die Schrittgröße dar)
Diese Formel wird immer iterativ ausgeführt, bis Konvergenz erreicht ist (


 nimmt in jeder Iteration ab, wenn der bei einem bestimmten Schritt reduzierte Wert kleiner als ein kleiner Wert ist
nimmt in jeder Iteration ab, wenn der bei einem bestimmten Schritt reduzierte Wert kleiner als ein kleiner Wert ist  (ist kleiner als 0,001), dann wird es als konvergent beurteilt) oder bis eine bestimmte Stoppbedingung erreicht ist (z. B. wenn die Anzahl der Iterationen einen bestimmten angegebenen Wert erreicht oder der Algorithmus einen bestimmten zulässigen Fehlerbereich erreicht).
(ist kleiner als 0,001), dann wird es als konvergent beurteilt) oder bis eine bestimmte Stoppbedingung erreicht ist (z. B. wenn die Anzahl der Iterationen einen bestimmten angegebenen Wert erreicht oder der Algorithmus einen bestimmten zulässigen Fehlerbereich erreicht).
2. Vektorisierungslösung
Die Vektorisierung verwendet Matrixberechnungen anstelle von for-Schleifen, um den Berechnungsprozess zu vereinfachen und zu verbessern Effizienz. Wie in der obigen Formel gezeigt, ist Σ(...) ein Summierungsprozess, der offensichtlich eine m-malige Schleife einer for-Anweisung erfordert, sodass die Vektorisierung überhaupt nicht vollständig implementiert ist. Der Vektorisierungsprozess wird im Folgenden vorgestellt:
Die Matrixform der Trainingsdaten ist wie folgt vereinbart: Jede Zeile von x ist ein Trainingsmuster und jede Spalte hat einen anderen Sonderwert :

Der Parameter A von g(A) ist ein Spaltenvektor, Wenn Sie also die g-Funktion implementieren, müssen Sie Spaltenvektoren als Argumente unterstützen und Spaltenvektoren zurückgeben. Aus der obigen Formel ist ersichtlich, dass hθ(x)-y aus g(A)-y in einem Schritt berechnet werden kann.
Der Theta-Aktualisierungsprozess kann wie folgt geändert werden:

Zusammenfassend lauten die Schritte zum Aktualisieren von θ nach der Vektorisierung wie folgt:
(1) Finden Sie A=X* θ(Dies ist eine Matrixmultiplikation, X ist ein (m, n+1)-dimensionaler Vektor, θ ist ein (n+1, 1)-dimensionaler Spaltenvektor und A ist ein (m, 1)-dimensionaler Vektor) 🎜> (2 ) Finden Sie E=g(A)-y (E, y sind (m,1) dimensionale Spaltenvektoren)
(3) Finden Sie (a stellt die Schrittgröße dar)

3, die Wahl der Schrittgröße a
a Der Wert von ist auch ein wichtiger Punkt, um die Konvergenz des Gradientenabfalls sicherzustellen. Wenn der Wert zu klein ist, ist die Konvergenz langsam, und wenn der Wert zu groß ist, ist die Konvergenz des iterativen Prozesses (Überschreiten des Mindestwerts) nicht garantiert. Um sicherzustellen, dass der Gradientenabstiegsalgorithmus korrekt funktioniert, muss sichergestellt werden, dass J(θ) in jeder Iteration abnimmt. Wenn der Wert der Schrittweite a korrekt ist, sollte J(θ) immer kleiner werden. Daher ist das Kriterium zur Beurteilung des Werts von a: Wenn J(θ) kleiner wird, zeigt dies an, dass der Wert korrekt ist, andernfalls verringern Sie den Wert von a.
Die Erfahrung bei der Auswahl der Schrittgröße a ist: Wählen Sie einen Wert von a, jedes Mal etwa das Dreifache der vorherigen Zahl. Wenn die Iteration nicht normal ablaufen kann (J steigt, ist die Schrittgröße zu groß und überschreitet die Boden der Schüssel) ), erwägen Sie die Verwendung einer kleineren Schrittweite. Wenn die Konvergenz langsam ist, sollten Sie erwägen, die Schrittweite zu erhöhen:
…, 0,001, 0,003, 0,01, 0,03, 0,1, 0,3, 1….
4, Eigenwertnormalisierung
Logistische Regression ist auch ein Regressionsalgorithmus, der mehrdimensionale Merkmalstrainingsdaten verwendet Bei der Gradientenmethode zur Lösung der Regression müssen die Eigenwerte skaliert werden, um sicherzustellen, dass der Wertebereich des Merkmals innerhalb derselben Skala liegt, bevor der Berechnungsprozess konvergiert (da der Eigenwertbereich beispielsweise sehr unterschiedlich sein kann) Merkmalswert 1 ist (1000-2000), der Wert von Merkmal 2 ist (0,1-0,2)). Die Methode der Feature-Skalierung kann angepasst werden:
1) Mittelwertnormalisierung (oder Standardisierung)
(X – Mittelwert). (X ))/std(X), std(X) stellt die Standardabweichung der Stichprobe dar
2) Neuskalierung
(X - min) / (max - min)
5, Algorithmusoptimierung – stochastische Gradientenmethode
Gradientenaufstieg (Abstiegs-)Algorithmus Der gesamte Datensatz muss jedes Mal durchlaufen werden, wenn die Regressionskoeffizienten aktualisiert werden. Diese Methode ist in Ordnung, wenn etwa 100 Datensätze verarbeitet werden. Wenn es jedoch Milliarden von Stichproben und Zehntausende von Merkmalen gibt, erhöht sich die Rechenkomplexität Methode wird zu hoch sein. Eine verbesserte Methode besteht darin, die Regressionskoeffizienten jeweils nur mit einem Abtastpunkt zu aktualisieren, was als stochastischer Gradientenalgorithmus bezeichnet wird. Da der Klassifikator beim Eintreffen neuer Proben schrittweise aktualisiert werden kann, kann er die Parameteraktualisierungen abschließen, ohne dass der gesamte Datensatz für die Stapelverarbeitung erneut gelesen werden muss. Daher handelt es sich beim stochastischen Gradientenalgorithmus um einen Online-Lernalgorithmus. (Entsprechend dem „Online-Lernen“ wird die Verarbeitung aller Daten auf einmal als „Stapelverarbeitung“ bezeichnet.) Der stochastische Gradientenalgorithmus entspricht dem Gradientenalgorithmus, ist jedoch recheneffizienter.
(3) Implementieren des logistischen Regressionsalgorithmus in Python
Im vorherigen Abschnitt haben wir etwas über J(θ) gelernt ) Durch Andrew Ngs Kurs =-(1/m)l(θ) wird die Gradientenabstiegsmethode gelöst, die den Lösungsprozess der logistischen Regression veranschaulicht. In diesem Abschnitt verwendet der Prozess der Implementierung des Algorithmus in Python immer noch direkt den Gradienten Aufstiegsmethode oder stochastische Gradientenaufstiegsmethode zur Lösung von J(θ) Das Objekt implementiert auch den Lösungsprozess mithilfe der Gradientenaufstiegsmethode oder der stochastischen Gradientenaufstiegsmethode.
Das LR-Klassifikator-Lernpaket enthält drei Module: lr.py/object_json.py/test.py. Das lr-Modul implementiert den LR-Klassifizierer über das Objekt logisticRegres und unterstützt zwei Lösungsmethoden: gradAscent('Grad') und randomGradAscent('randomGrad') (wählen Sie eine der beiden, classifierArray speichert nur ein Klassifizierungslösungsergebnis, natürlich können Sie das auch Definiere zwei classifierArray unterstützt beide Lösungsmethoden.
Das Testmodul ist eine Anwendung, die den LR-Klassifikator nutzt, um die Sterblichkeit kranker Pferde anhand der Herniensymptome vorherzusagen. Bei diesen Daten liegt ein Problem vor: Die Daten weisen eine Verlustrate von 30 % auf, die durch den Sonderwert 0 ersetzt wird, da 0 keinen Einfluss auf die Gewichtsaktualisierung des LR-Klassifikators hat.
Das teilweise Fehlen von Beispielmerkmalswerten in den Trainingsdaten ist ein sehr heikles Problem. Viele Literaturen widmen sich der Lösung dieses Problems, weil es schade ist, die Daten wegzuwerfen direkt, und die Kosten für die Wiederanschaffung sind ebenfalls hoch. Zu den optionalen Methoden zur Behandlung fehlender Daten gehören:
□ Verwenden Sie den Mittelwert der verfügbaren Funktionen, um fehlende Werte zu füllen.
□ Verwenden Sie spezielle Werte zu ±True-Komplement fehlender Werte, z. B. -1;
□ Ignorieren Sie Stichproben mit fehlenden Werten.
□ Verwenden Sie den Mittelwert ähnlicher Stichproben, um fehlende Werte auszufüllen □ Verwenden Sie zusätzliche Algorithmen für maschinelles Lernen, um fehlende Werte vorherzusagen.
Die Download-Adresse des Lernpakets für den LR-Klassifikatoralgorithmus lautet:
Logistische Regression für maschinelles Lernen
(4) Anwendung der logistischen Regression
Der Hauptzweck der logistischen Regression:
Suche nach Gefahrenfaktoren: Suche nach Risikofaktoren für eine bestimmte Krankheit usw.
Vorhersage: Prognostizieren Sie anhand des Modells die Wahrscheinlichkeit einer bestimmten Krankheit oder Situation unter verschiedenen unabhängigen Bedingungen Variablen;
Diskriminierung: Tatsächlich ähnelt es in gewisser Weise der Vorhersage. Es basiert auch auf dem Modell, um die Wahrscheinlichkeit zu bestimmen, dass jemand zu einer bestimmten Krankheit oder einer bestimmten Situation gehört Es geht darum, herauszufinden, wie wahrscheinlich es ist, dass diese Person beim Sex an einer bestimmten Krankheit leidet.
Logistische Regression wird hauptsächlich in der Epidemiologie verwendet, um die Risikofaktoren einer bestimmten Krankheit zu untersuchen, die Wahrscheinlichkeit einer bestimmten Krankheit basierend auf den Risikofaktoren vorherzusagen usw. Wenn Sie beispielsweise die Risikofaktoren für Magenkrebs untersuchen möchten, können Sie zwei Personengruppen auswählen, eine ist die Gruppe mit Magenkrebs und die andere ist die Gruppe mit Nicht-Magenkrebs. Die beiden Personengruppen müssen unterschiedliche körperliche Merkmale haben Zeichen und Lebensstile. Die abhängige Variable ist hier, ob es sich um Magenkrebs handelt, also „ja“ oder „nein“. Die unabhängigen Variablen können viele umfassen, wie zum Beispiel Alter, Geschlecht, Essgewohnheiten, Helicobacter-pylori-Infektion usw. Die unabhängigen Variablen können entweder kontinuierlich oder kategorisch sein.
Verwandte Empfehlungen:
Logistische Regressionsleiterabstiegsberechnung zur Berechnung des Maximalwerts
Umfassendes Verständnis von LR
Eine kurze Beschreibung der Prinzipien gängiger Algorithmen für maschinelles Lernen (LDA, CNN, LR)
Das obige ist der detaillierte Inhalt vonPython implementiert den klassischen LR-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

