Turm von Hanoi und Fibonacci-Sequenz in Python basierend auf einem rekursiven Algorithmus implementiert

Dieser Artikel stellt hauptsächlich den Turm von Hanoi und die von Python basierende Fibonacci-Sequenz vor. Er analysiert die rekursiven Implementierungstechniken des Turms von Hanoi und der Fibonacci-Sequenz in Form von Beispielen dazu

Dieser Artikel beschreibt die in Python implementierten Tower of Hanoi- und Fibonacci-Sequenzen basierend auf rekursiven Algorithmen. Teilen Sie es als Referenz mit allen. Die Details lauten wie folgt:

Hier verwenden wir zwei Beispiele, um die Verwendung der Rekursion in Python zu erlernen.

1. Finden Sie die Zahl mit dem Index n in der Fibonacci-Folge (der Index zählt von 0)

Die Form der Fibonacci-Folge ist So: 0,1,1,2,3,5,8,13...

① Bei Verwendung der while-Schleife lautet der Python2-Code wie folgt:

def fib(n):
  a,b=0,1
  count=0
  while count<n:
    a,b=b,a+b
    count=count+1
  print a

Die laufenden Ergebnisse sind wie folgt:

>>> >0
> >> fib(1)
>>> fib(2)
>>> 🎜>2
> ;>> fib(4)
3
>>> fib(5)
5



② Rekursion verwenden (Rekursion muss Randbedingungen sein)

, der Python2-Code lautet wie folgt:

def fib(n):
  if n==0 or n==1:#递归的边界条件
    return n
  else:
    return fib(n-1)+fib(n-2)

Die laufenden Ergebnisse sind wie folgt:

>>> fib(0)

0

>>> fib(1)

1

>> ;> fib(2)
1
>>> fib(3)
>>> >> fib(5)
5


Rekursion ist einer der Algorithmen, der rechnerisches Denken am besten ausdrückt und uns den Ausführungsprozess der Rekursion ansieht :

Für dasselbe Programm ist die Ausführungseffizienz der Rekursion geringer als die der Schleife und der Systemressourcenverbrauch höher, obwohl das Programm einfach ist und die Rekursion verwendet der Schleife. Da die Rekursion Schicht für Schicht aufgerufen und nach Abschluss Schicht für Schicht zurückgegeben wird, ist die Ausführungseffizienz der Rekursion nicht hoch. Warum also Rekursion verwenden? Da es einige Probleme gibt, können wir keine sehr offensichtliche Schleifenlösung finden, aber es ist einfach, eine offensichtliche rekursive Lösung zu finden. Nehmen wir zum Beispiel das berühmte Turmproblem von Hanoi.

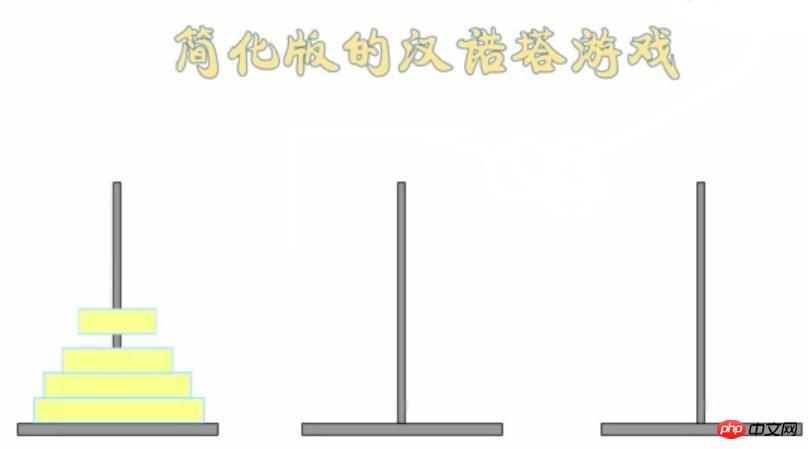
2. Tower of Hanoi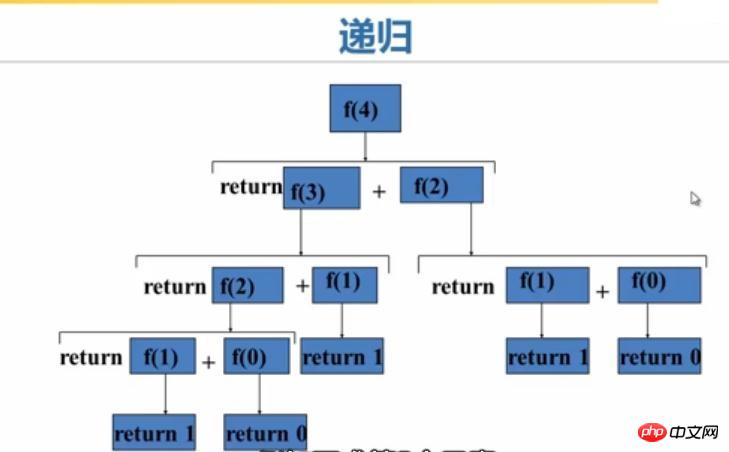

Das Bild unten ist eine vereinfachte Version des Tower of Hanoi-Spiels mit nur 4 Platten:

Die Regeln des Tower of Hanoi-Spiels lauten wie folgt:

Der Python2-Code lautet wie folgt:

Laufergebnis:

def hanoi(a,b,c,n):
  if n==1:#递归结束条件
    print a,'->',c
  else:
    hanoi(a,c,b,n-1)
    print a,'->',c
    hanoi(b,a,c,n-1)

>>> ','C',1)

A -> 🎜>A ->C
B ->>> >A -> B

A -> 🎜>

Verwandte Empfehlungen:


Python-Implementierung und -Anwendung des neuronalen Netzwerkalgorithmus (BP)

Das obige ist der detaillierte Inhalt vonTurm von Hanoi und Fibonacci-Sequenz in Python basierend auf einem rekursiven Algorithmus implementiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!