Heim >Backend-Entwicklung >Python-Tutorial >Python-Beispiel zum Ermitteln des größten gemeinsamen Teilers basierend auf der euklidischen Division
Python-Beispiel zum Ermitteln des größten gemeinsamen Teilers basierend auf der euklidischen Division
- 不言Original
- 2018-04-04 16:52:097048Durchsuche
In diesem Artikel wird hauptsächlich Pythons Methode zur Lösung des größten gemeinsamen Teilers basierend auf der euklidischen Divisionsmethode vorgestellt. Er analysiert die Implementierungsmethode und die Optimierungsoperationsfähigkeiten von Python mithilfe der euklidischen Divisionsmethode, um den größten gemeinsamen Teiler in Form von Beispielen zu lösen. Freunde, die es brauchen, können darauf verweisen
Das Beispiel in diesem Artikel beschreibt Pythons Methode zur Lösung des größten gemeinsamen Teilers basierend auf der euklidischen Divisionsmethode. Teilen Sie es als Referenz mit allen. Die Details lauten wie folgt:
Ich habe die Lösung des größten gemeinsamen Teilers in Knuth TAOCP bereits zusammengefasst. Tatsächlich ist die in den außerschulischen Fragen erforderliche Algorithmusmodifikation so Lösen Sie den größten gemeinsamen Teiler durch euklidische Division.
Mein anfängliches Verständnis dieser Frage war falsch und natürlich hatte ich keine Standardantwort. Schreiben Sie nun die entsprechende Code-Implementierung gemäß der Standardantwort:
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(55,120))
Das Ausführungsergebnis des Programms:
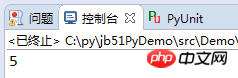
Vertauschen Sie die Positionen der beiden Zahlen. Der Code lautet wie folgt:
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(120,55))
Das Ausführungsergebnis des Programms:

In der Frage wurde erwähnt, dass dadurch die Effizienz verringert wird. Nach dem obigen Code zu urteilen, sollte der Effizienzverlust in der Teilung und im Urteil liegen. Nehmen Sie hier den Code des vorherigen Algorithmus und vergleichen Sie ihn:
def CommDevisor(m,n):
r = m % n
while r != 0:
m = n
n = r
r = m % n
return n
print(CommDevisor(120,25))
Laufergebnisse:
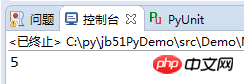
Der neue Algorithmus verfügt über eine zusätzliche Divisions- und Vergleichsoperation in der Schleife. Tatsächlich ist die Vergleichseffizienz immer noch gut, aber die Divisionsoperation führt zu einer Verringerung der Effizienz.
PS: Hier sind ein paar weitere Berechnungstools, die Ihnen als weitere Referenz empfohlen werden:
Online-Unärfunktion (Gleichung ) Lösungsberechnungstools:
http://tools.jb51.net/jisuanqi/equ_jisuanqi
Wissenschaftlicher Rechner online verwenden_erweiterter Rechner Online-Berechnung:
http://tools.jb51.net/jisuanqi/jsqkexue
Online-Rechner_Standardrechner:
http://tools. jb51.net/jisuanqi/jsq
Verwandte Empfehlungen:
Wie man mit Python den größten gemeinsamen Teiler löst
Das obige ist der detaillierte Inhalt vonPython-Beispiel zum Ermitteln des größten gemeinsamen Teilers basierend auf der euklidischen Division. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

