So identifizieren Sie Linearität in der Python-Programmierung

In diesem Artikel erfahren Sie hauptsächlich, wie Sie Linearität in der Python-Programmierung unterscheiden können. Freunde, die es brauchen, können einen Blick darauf werfen.

"""
Author: Victoria
Created on: 2017.9.15 11:45
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def LDA(X0, X1):
    """
    Get the optimal params of LDA model given training data.
    Input:
        X0: np.array with shape [N1, d]
        X1: np.array with shape [N2, d]
    Return:
        omega: np.array with shape [1, d]. Optimal params of LDA.
    """
    #shape [1, d]
    mean0 = np.mean(X0, axis=0, keepdims=True)
    mean1 = np.mean(X1, axis=0, keepdims=True)
    Sw = (X0-mean0).T.dot(X0-mean0) + (X1-mean1).T.dot(X1-mean1)
    omega = np.linalg.inv(Sw).dot((mean0-mean1).T)
    return omega
if __name__=="__main__":
    #read data from xls
    work_book = pd.read_csv("../data/watermelon_3a.csv", header=None)
    positive_data = work_book.values[work_book.values[:, -1] == 1.0, :]
    negative_data = work_book.values[work_book.values[:, -1] == 0.0, :]
    print (positive_data)
    #LDA
    omega = LDA(negative_data[:, 1:-1], positive_data[:, 1:-1])
    #plot
    plt.plot(positive_data[:, 1], positive_data[:, 2], "bo")
    plt.plot(negative_data[:, 1], negative_data[:, 2], "r+")
    lda_left = 0
    lda_right = -(omega[0]*0.9) / omega[1]
    plt.plot([0, 0.9], [lda_left, lda_right], 'g-')
    plt.xlabel('density')
    plt.ylabel('sugar rate')
    plt.title("LDA")
    plt.show()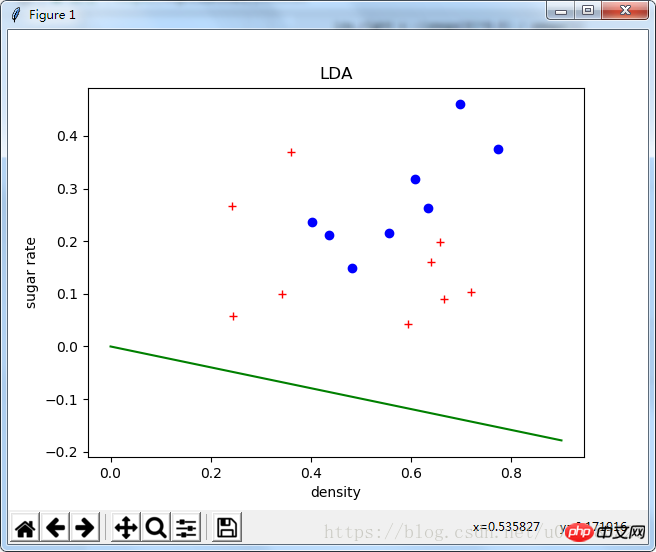

Verwandte Empfehlungen:

Eine kurze Einführung in Linear Diskriminanzanalyse-Tutorial

Lineare Diskriminanzanalyse

Das obige ist der detaillierte Inhalt vonSo identifizieren Sie Linearität in der Python-Programmierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!