Ausführliche Erläuterung der regelmäßigen digitalen Verifizierung (mit Code)

Dieses Mal erkläre ich Ihnen, was die Vorsichtsmaßnahmen sind. Hier ist ein praktischer Fall, werfen wir einen Blick darauf.

Teil 1: Numerische Überprüfung

1. Überprüfen Sie Zeichenfolgen, die nur Zahlen und die angegebene Länge (N) enthalten

Wenn ich beispielsweise eine Zeichenfolge überprüfen möchte, die nur Zahlen und eine Länge von 6 enthält, z. B. 123456, kann ich die folgenden Überprüfungsmethoden mit demselben Effekt verwenden

\d{6}
[0-9]{6}
\d\d\d\d\d\d

Die oben genannten Methoden haben den gleichen Effekt. Die erste Methode ist empfehlenswerter und prägnanter! Hinweis: Ich werde später den prägnanteren regulären Ausdruck verwenden, ohne zu ausführlich zu sein!

2. Stellen Sie sicher, dass die Wortzeichenfolge nur Zahlen enthält und geben Sie die Bereichslänge (N-M) an.

Ich möchte beispielsweise überprüfen, dass sie nur Zahlen enthält Die Länge liegt zwischen 5 und 8 Zeichenfolgen, z. B. 12345, 123456, 1234567, 12345678. Sie können die Überprüfungsmethode

3 verwenden

Offensichtlich sind 0, 100, 56 usw. allesamt nicht negative ganze Zahlen, während -12, 0135 usw. keine nicht negativen ganzen Zahlen sind. Die Verifizierungsdemonstration lautet wie folgt:

                                                                                                                                                                                           56 wird nicht ausgewählt, da es sich nicht um eine positive Zahl handelt. (Hinweis: ^ wird verwendet, was bedeutet, dass es mit 0 oder [1-9] beginnen muss, daher wird -56 nicht ausgewählt; wenn kein ^ vorhanden ist, wird 56 in -56 ausgewählt)

4. Überprüfung beliebiger Ganzzahlen

Beliebige Ganzzahlen wie 0, 456, -65 usw. Dies sind beliebige Ganzzahlen, was bedeutet, dass wir positive und nicht negative Ganzzahlen kombinieren müssen Die Verifizierungsdemonstration lautet wie folgt:

　

Es werden also alle positiven Zahlen einschließlich 0, positive ganze Zahlen und negative ganze Zahlen abgeglichen.

5. Überprüfung positiver Ganzzahlen innerhalb des angegebenen Bereichs

Zum Beispiel möchten wir positive Ganzzahlen im Bereich von 1-5678 überprüfen, z. B. 465, 23 , 5677 usw. Es gehört zu diesem Bereich. Wie kann ich das überprüfen? Keine Sorge, wir können zwischen Partitionen überprüfen:

Verwenden Sie b[1-9]d{0-2}b, um alle positiven ganzen Zahlen zwischen 1-999 zu überprüfen
Verwenden Sie b[1-4]d{3}b, um alle positiven ganzen Zahlen zwischen 1000 und 4999 zu überprüfen
Verwenden Sie b5[0-5] d{ 2}b, um alle positiven Ganzzahlen zwischen 5000 und 5599 zu überprüfen
Verwenden Sie b56[0-6]db, um alle positiven Ganzzahlen zwischen 5600 und 5669 zu überprüfen
Verwenden Sie b567[0-8]b, um alle positiven ganzen Zahlen zwischen 5670 und 5678 zu überprüfen.
Zusammenfassend können wir den folgenden regulären Ausdruck verwenden, um alle positiven ganzen Zahlen zwischen 1 zu überprüfen -5678:

Aber ist das wirklich so? Die Verifizierung läuft wie folgt ab:

^([1-9]\d{0,2})|([1-4]\d{3})|(5[0-5]\d{2})|(56[0-6]\d)|(567[0-8])$

　

Warum ist das so? ? ? Die Überprüfung der nächsten drei Zahlen ist nicht der gewünschte Effekt! ! Dies liegt daran, dass der reguläre Ausdruck beim Abgleich von links nach rechts übereinstimmt. Unter diesen können 2602 und 4999 mit [1-9]d{0,2} abgeglichen werden, sodass keine Notwendigkeit besteht, fortzufahren.

Versuchen wir, die Reihenfolge der regulären Ausdrücke umzukehren? Wie unten gezeigt:

Der Effekt ist wie folgt:

^(567[0-8])|(56[0-6]\d)|(5[0-5]\d{2})|([1-4]\d{3})|([1-9]\d{0,2})$

Was uns dieses Mal glücklich macht, ist, dass alle Zahlen zwischen 1-5678 ausgewählt wurden Habe es! ! Aber 5 von 789 und -5 wurden ausgewählt. Dies liegt daran, dass wir vor der ersten Gruppierung nur ^ hinzugefügt haben. Wir müssen vor jeder Gruppierung ^ hinzufügen. Wie unten gezeigt:

Diesmal ist der Effekt kein Problem, wie folgt:

^(567[0-8])|^(56[0-6]\d)|^(5[0-5]\d{2})|^([1-4]\d{3})|^([1-9]\d{0,2})$

Daraus ist ersichtlich: das Prinzip der Kombinationsreihenfolge (positive ganze Zahl): Von der Bereichskombination des Maximalwerts bis zur Bereichskombination des Minimalwerts.

从这个例子受到启发，我们对于指定范围内的正整数的验证的第一个例子中的每一个分组后添加$或\b也可以解决问题。

也就是说下面的两行代码均有效：

^(567[0-8])|^(56[0-6]\d)|^(5[0-5]\d{2})|^([1-4]\d{3})|^([1-9]\d{0,2})$
^([1-9]\d{0,2})$|([1-4]\d{3})$|(5[0-5]\d{2})$|(56[0-6]\d)$|(567[0-8])$

6.实数的验证

这里要介绍的实数的验证是至少包含一个小数点的实数，因此实数就包括了整数部分、小数部分和小数点。

 验证方法如下：

-?(0|([1-9]\d*))\.\d+

其中-?表示可以有负号也可以没有负号，（0|[1-9]\d*）表示整数部分可以是0也可以是不以0开头的其他整数，\.是为了对元字符.进行转义，\d+表示在小数点后面可以有1个或多个数字重复。所以它可以用来验证一般形式的实数（如0.0、1.2、-1.20等），还可以用来验证负0，如-0.0、-0.00等。

如果我们希望验证指定精度的实数，我们只需要把末尾的+修改成相应的精度即可，如下所示：

-?(0|([1-9]\d*))\.\d{3}$

即表示小数部分长度为3的实数。

7.科学计数法的验证

科学计数法就是把一个数记成a*10^n的形式。其中，a是一位整数或着是只有一位整数的小数（如5,3.2等等），所以可知1<=|a|<10。而n是一位整数。所以不难得出科学计数法的验证方法如下所示：

^-?[1-9](\.\d+)？\*10\^-?\d+$

第二部分：4种国内电话号码的验证

我们知道中国的电话号码的形式不外乎有下面四种：

1.手机号码

2.固定电话号码（不包括区号）

3.区号+固定电话号码

4.区号+固定电话号码+分机号

下面我们按照顺序逐一介绍

1.手机号码

目前国内的手机号码多是13开头、15开头和18开头，并且第三位数字目前都有【0-9】这10个数，所以验证起来就很简单了。如下所示：

     

显然第二种方法更简单一些。

 2.固定电话号码（不包括区号）

固定电话号码一般为7位（如2268358）或8位（82668110），所以验证起来是非常简单的，如下所示：

 

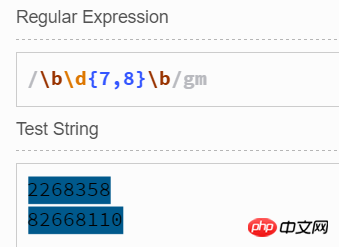
但是，某个地区的电话号码往往是固定在一个具体的范围里的，比如新疆石河子某个地区为2268001-2268999，这时想要确定就需要稍微花一些功夫了。

我们可以把2268001-2268999划分为2268001-2268009和2268010-2268099和2268100-2268999。这样，把验证三者的正则表达式组合起来即可。如下所示：

2268((00[1-9])|(0[1-9]\d)|([1-9]\d{2}))

 

PS 这里就不具体介绍啦，都是很简单的知识，如果有疑问可以看我的上一篇博文，它对基本知识阐述得很具体。

3.区号+固定电话号码验证

区号的长度一般为3-4位，固定电话号码的长度一般为7-8位，比如029-82668110为3位区号和8位固定电话号码的组合，0993-2268358是4位区号和7位固定号码的组合。且在区号和固定号码之间一般都是由-（连字符）链接的。可知，我们只需要对区号和固定电话分别验证即可。　　

\b0\d{2,3}[- ]?\d{7,8}\b

演示效果如下：

 

4.区号+固定电话号码验证+分机号码验证

一些比较大的公司、企业或者政府部门在向外部提供固定的电话号码是，除了区号、固定电话号码之外，还可能包括分机号码。

下面我们以4位的分级号码为例。一般在分机号码之前可能是空格，也可能是-（连字符），还可能什么都没有。 于是验证方法如下：

\b0\d{2,3}[- ]?\d{7,8}[- ]?\d{4}\b

演示效果如下：

    

第三部分：2种身份证号码的验证

1.基本知识

15位身份证号码：

1985年我国实行居民身份证制度，当时签发的身份证号码是15位的。其中前6位为地址码，中间6位为出生日期码（年月日各用两位数字表示），最后三位为顺序码。

(注：顺序码是对同年、同月、同日出生的人编订序号，顺序码的奇数分配给男性，偶数分配给女性)

18位身份证号码：

1999年我国开始使用18位的身份证号。其中前6位为地址码，中间8位为出生日期码（年用4位表示，月日各用2位表示），最后四位为顺序码和校验码。

（注：年份用4位是因为使用2位会导致冲突，比如1903年和2003年出生的人。而校验码主要是为了校验计算机输入公民身份证号码的前17位数字是否正确，其取值范围是0至10，当值等于10时，用X表示）

 2. 15位身份证号码的验证

前6位地址码可以为任意数字，78位的年份码为任意数字，9和10位的月份码应当在01-12之间，11和12位的日期码在01-31之间，最后三位的顺序码为长度为3的任意字符串。于是验证方法如下:

复制代码 代码如下:

\b\d{8}(0[1-9]|1[012])(0[1-9]|[12]\d|3[01])\d{3}\b

 3. 18位身份证号码的验证

前6位地址码为任意数字，7-10位的年份码前两位以19或20开头（这里就不考虑18开头了），月日同15位的身份证号码，三位顺序码为长度为3的任意字符串，最后以为验证码为0-9或X。于是验证方法如下：

\b\d{6}(19|20)\d{2}(0[1-9]|1[012])(0[1-9]|[12]\d|3[01])\d{3}(\d|X)\b

因为只要知道了思路，正则表达式写出来并不难，所以这里就不细讲了。

 第四部分：邮政编码验证

我国邮政编码的编码规则:我国采用四级六位编码制，前两位表示省、市、自治区，第三位代表邮区，第四位代表县、市，最后两位代表投递邮局，最后两位是代表从这个城市哪个投递区投递的，即投递区的位置。例如:邮政编码“130021”“13”代表吉林省，“00”代表省会长春，“21”代表所在投递区。

因此验证我国的邮政编码就十分方便了，如下所示：

     

第五部分：两种IP地址的验证

IP地址可以简单验证，还可以精确验证。

1.简单IP地址验证

我首先ping到了http://www.jb51.net/的IP地址：42.121.252.58。 实际上IP地址一般是1~3位整数.1~3位整数.1~3位整数.1~3位整数，于是我们可以通过下面的正则表达式作简单验证：

([1-9]\d{0,2}\.){3}[1-9]\d{0,2}

验证效果如下所示：

 

2.精确IP地址验证

显然，上面的简单IP地址验证是不精确的，比如999.999.999.999这就不是一个正确的IP地址。

我们知道32位IP地址的每一个数值都是在0~255之间，所以对于1~3位整数.1~3位整数.1~3位整数.1~3位整数我们应该将整数限制在0~255之间，显然，这里要使用分区间的方法了。

0-99之间可以这样表示：([1-9]\d?)|0              (注意这里的表示方法，如果这个数不为0，那么前面就不能有0)

100-199 kann wie folgt ausgedrückt werden: 1d{2}

200-249 kann wie folgt ausgedrückt werden: 2[0-4]d

250-255 Das bedeutet: 25[0-5]

Zusammenfassend lässt sich sagen, dass die Methode zur korrekten Überprüfung der IP-Adresse wie folgt lautet:

Kopieren Sie den Code Der Code lautet wie folgt :

(((25[0-5])|2[0-4]d|1d{2}|[1-9]d|0).){3}(( 25[0 -5])|2[0-4]d|1d{2}|[1-9]d|0)

Der Demonstrationseffekt ist wie folgt:

Es ist erwähnenswert, dass die Gruppierung entscheidend ist. Nur wenn Sie die Gruppe in die richtige Gruppe einteilen, kann es keine Probleme geben.

Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, dass er für das Lernen aller hilfreich sein wird. Ich hoffe auch, dass jeder Script Home unterstützt.

Ich glaube, dass Sie die Methode beherrschen, nachdem Sie den Fall in diesem Artikel gelesen haben. Weitere spannende Informationen finden Sie in anderen verwandten Artikeln auf der chinesischen PHP-Website!

Empfohlene Lektüre:

Detaillierte Erläuterung der Verwendung des g-Modifikators für reguläre globale Übereinstimmungsmuster

Regulärer Ausdruck m-Modifikator (Mehrzeiliger Abgleich) Detaillierte Erläuterung der Verwendung

Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung der regelmäßigen digitalen Verifizierung (mit Code). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!