Heim >Web-Frontend >js-Tutorial >Wie raphael.js die Konvertierung von Winkel in Bogenmaß implementiert
Wie raphael.js die Konvertierung von Winkel in Bogenmaß implementiert
- 零到壹度Original
- 2018-03-28 16:58:162382Durchsuche
Dieser Artikel zeigt Ihnen hauptsächlich, wie Sie Winkel und Bogenmaß in raphael.js umrechnen. Er hat einen guten Referenzwert und ich hoffe, dass er für alle hilfreich sein wird. Folgen wir dem Herausgeber und werfen wir einen Blick darauf.
Die Beziehung zwischen Bogenmaß und Winkel
1. Zwei Winkeleinheiten
“ Bogenmaß „“ und „Grad“ sind zwei verschiedene Einheiten zur Messung der Winkelgröße. Genauso wie „Meter“ und „Fuß“ zwei unterschiedliche Maßeinheiten für die Länge sind.
In Flash ist festgelegt, dass der Winkel im Rotationswinkel (Rotation) in „Grad“ als Einheit angegeben werden sollte, während der Winkel in der trigonometrischen Funktion in „Bogenmaß“ als Einheit angegeben werden sollte. Diese Regel ist das Erste, woran wir uns erinnern müssen! ! ! Zum Beispiel: rotation2 – ist eine Drehung von „2 Grad“; sin (π/2) – ist der Sinus eines Winkels mit einer Größe von „π/2 Bogenmaß“.
2. Die Definition des Bogenmaßes
Die sogenannte „Definition des Bogenmaßes“ bedeutet, wie wird die Winkelgröße von 1 Bogenmaß definiert?
Wir wissen, dass die Definition von „Grad“ lautet: „Zwei Strahlen werden vom Mittelpunkt des Kreises zum Umfang ausgesendet und bilden einen eingeschlossenen Winkel und einen Bogen, der dem eingeschlossenen Winkel direkt gegenüberliegt. Wenn die Länge dieses Bogens genau ist.“ entspricht einem 360stel des Kreisumfangs. Der Winkel zwischen den beiden Strahlen beträgt 1 Grad (Abbildung 1)
Wie ist das Bogenmaß definiert? Zwei Strahlen schießen von der Mitte nach der Umfang, der einen eingeschlossenen Winkel und einen eingeschlossenen Winkel bildet. Wenn die Länge dieses Bogens genau dem Radius des Kreises entspricht, beträgt der Winkel zwischen den beiden Strahlen 1 Bogenmaß.
Vergleichen Sie diese beiden Definitionen von Grad und Bogenmaß. Der einzige Unterschied zwischen ihnen besteht darin, dass die Länge des durch den Winkel begrenzten Bogens einem Drittel des Kreisumfangs entspricht, während das Bogenmaß einfach dem Radius entspricht Die Definition des Bogenmaßes lautet: Wenn die Länge des durch den Winkel begrenzten Bogens gleich dem Radius ist, beträgt die Größe des Winkels 1 Bogenmaß. Die relevanten Bilder zu diesem Thema lauten wie folgt:
Wenn die Länge des durch den Winkel begrenzten Bogens ein Vielfaches des Radius beträgt, beträgt die Größe des Winkels nur ein paar Bogenmaße. Ihr Verhältnis kann wie folgt ausgedrückt und berechnet werden Formel: 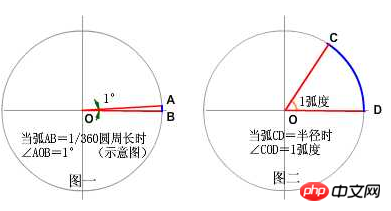 Winkel (Bogenmaß) = Bogenlänge/Radius
Winkel (Bogenmaß) = Bogenlänge/Radius
Der Umfang eines Kreises ist 2π mal der Radius, also beträgt ein Umfangswinkel (360 Grad) 2π Bogenmaß
Die Länge eines Halbkreises ist π mal dem Radius, also ist ein gerader Winkel π Bogenmaß
3. Umrechnung zwischen Grad und Bogenmaß
Demnach ist ein gerader Winkel π Bogenmaß. 180 Grad = π Bogenmaß
Daraus können wir sehen:
1 Grad = π/180 Bogenmaß (≈0,017453 Bogenmaß)
Daher erhalten wir die Formel zur Umrechnung von Grad in Bogenmaß:
Bogenmaß = Grad 45×π/180 =π/4 Bogenmaß
30°=30×π/180 =π/6 Bogenmaß
120°=120×π/180 =2π/3 Bogenmaß
Das Bogenmaß wird wiederum Wie berechnet man Grad?
Weil π Bogenmaß = 180°
Also 1 Bogenmaß = 180°/π (≈57,3°)
Daher kann die Formel zur Umrechnung von Bogenmaß in Grad erhalten werden:
Grad = Bogenmaß × 180°/π
Zum Beispiel:
4π/3 Bogenmaß = 4π/3 ×180°/π
= 240°
Einige Freunde sagen vielleicht, dass es mit „π/“ multipliziert wird. 180". Oder „180°/π" ist leicht falsch zu verstehen. Tatsächlich muss man sich nur merken: π ist π Bogenmaß und 180 ist 180 Grad. In welche Einheit ich umrechnen möchte, muss ich angeben der Zähler. Um in Bogenmaß umzurechnen, setzen Sie π Bogenmaß auf den Zähler und multiplizieren Sie es mit π/180. Darüber hinaus ist 1 Grad viel kleiner als 1 Bogenmaß, nur etwa 0,017453 Bogenmaß (π/180≈0,017453). Daher muss die Zahl nach der Umrechnung von Grad in Bogenmaß kleiner werden, sodass sie bei der Umrechnung in Bogenmaß mit π/180 multipliziert werden muss. Wenn Sie so darüber nachdenken können, werden Sie keinen Fehler machen.
Schreiben Sie „π“ als „PI“ im AS-Code. Und da „π“ und „sin“ beide „mathematische Funktionen“ sind, muss gemäß den Vorschriften „Math“ (Math ist die Abkürzung für „Mathematik“ im Englischen) vorangestellt und dann als „Math.PI“ geschrieben werden ", "Math.sin".
Sin30° muss also als Math.sin (30*Math.PI/180) geschrieben werden. Der Teil in Klammern dient zur Umrechnung von 30° in Bogenmaß, also 30×π/180.
Verwandte Empfehlungen:
Umrechnung von Bogenmaßen und Winkeln
Verstehen Sie die Konzepte und Umrechnungsbeziehungen von Winkeln und Bogenmaßen
Das obige ist der detaillierte Inhalt vonWie raphael.js die Konvertierung von Winkel in Bogenmaß implementiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

