H5 realisiert einen rotierenden dreidimensionalen Zauberwürfel

Dieses Mal bringe ich Ihnen H5, um den rotierenden dreidimensionalen Zauberwürfel zu realisieren. Was sind die Vorsichtsmaßnahmen für H5, um den rotierenden dreidimensionalen Zauberwürfel zu realisieren? Schauen Sie mal rein.

Das Folgende ist der Vorschaubildschirm.

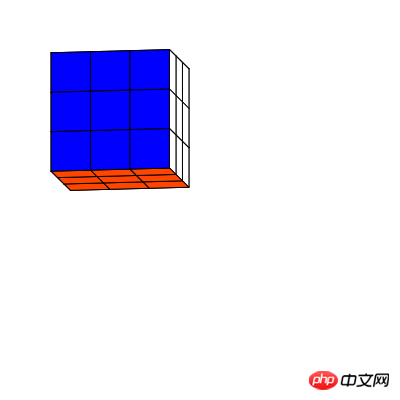
Produktionsprozess

Zuerst müssen Sie Html5 herunterladen Open-Source-Bibliothek lufylegend-1.4.0

Der Zauberwürfel ist in 6 Flächen unterteilt, jede Fläche besteht aus 9 kleinen Rechtecken. Jetzt kapsele ich jedes kleine Rechteck als Klasse,

Da es sich bei dem, was wir jetzt erstellen, um einen 3D-Zauberwürfel handelt, müssen wir zum Zeichnen jedes kleinen Rechtecks ​​die 4 Fixpunkte des kleinen Rechtecks ​​kennen, und diese 4 Fixpunkte werden entsprechend dem Rotationswinkel des Raums transformiert, also in Um diese 4 zu berechnen, müssen Sie für Festpunktkoordinaten den Drehwinkel des Zauberwürfels um die x- und z-Achse kennen.

Erstellen Sie also eine Rechteckklasse wie folgt:

function Rect(pointA,pointB,pointC,pointD,angleX,angleZ,color){  
    base(this,LSprite,[]);  
    this.pointZ=[(pointA[0]+pointB[0]+pointC[0]+pointD[0])/4,(pointA[1]+pointB[1]+pointC[1]+pointD[1])/4,(pointA[2]+pointB[2]+pointC[2]+pointD[2])/4];  
    this.z = this.pointZ[2];  
    this.pointA=pointA,this.pointB=pointB,this.pointC=pointC,this.pointD=pointD,this.angleX=angleX,this.angleZ=angleZ,this.color=color;  
}  
  
Rect.prototype.setAngle = function(a,b){  
    this.angleX = a;  
    this.angleZ = b;  
    this.z=this.getPoint(this.pointZ)[2];  
};

PunktA, PunktB, PunktC, PunktD sind die vier Eckpunkte des kleinen Rechtecks, WinkelX, WinkelZ sind die Drehwinkel des x -Achsen- bzw. Z-Achsen-Farbe ist die Farbe des kleinen Rechtecks.

Der Zauberwürfel ist in 6 Flächen unterteilt. Schauen wir uns zunächst die Vorderseite an. Wenn die Mitte des Würfels als Mittelpunkt des 3D-Koordinatensystems verwendet wird, dann die Koordinaten, die jedem festen Punkt entsprechen der 9 kleinen Rechtecke sind wie in der Abbildung unten dargestellt

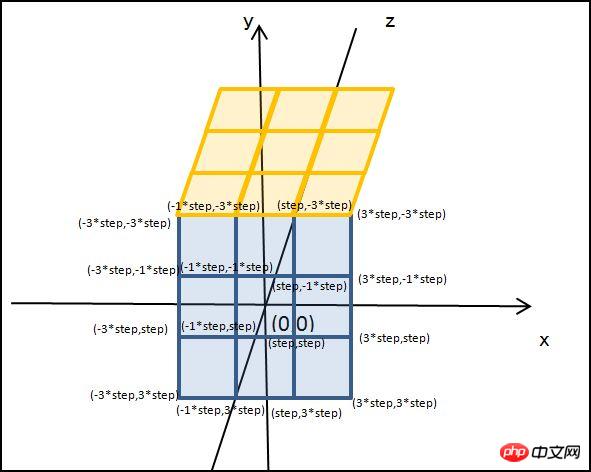
Die 9 kleinen Rechtecke auf der vorherigen Oberfläche können also mit dem folgenden Code erstellt werden

for(var x=0;x<3;x++){  
    for(var y=0;y<3;y++){  
        z = 3;  
        var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#FF0000");  
        backLayer.addChild(rect);  
    }  
}

Dabei ist backLayer eine LSprite-Klasse und step ist die Hälfte der Länge eines kleinen Rechtecks. Auf die gleiche Weise können Sie auch die anderen fünf Flächen erhalten.

Vor dem Zeichnen dieser sechs Flächen müssen zunächst die Koordinaten jedes Fixpunkts anhand des Drehwinkels berechnet werden

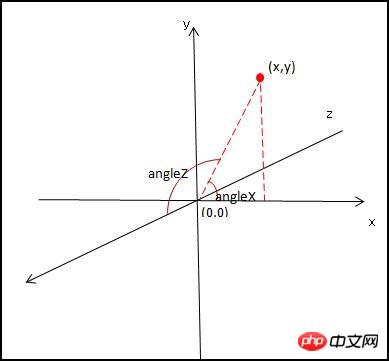
Verwenden Sie gemäß dem obigen Bild die folgende Formel, um die transformierten Festpunktkoordinaten zu erhalten

Rect.prototype.getPoint = function(p){  
    var u2,v2,w2,u=p[0],v=p[1],w=p[2];  
    u2 = u * Math.cos(this.angleX) - v * Math.sin(this.angleX);  
    v2 = u * Math.sin(this.angleX) + v * Math.cos(this.angleX);  
    w2 = w;  
    u = u2; v = v2; w = w2;  
    u2 = u;  
    v2 = v * Math.cos(this.angleZ) - w * Math.sin(this.angleZ);  
    w2 = v * Math.sin(this.angleZ) + w * Math.cos(this.angleZ);  
    u = u2; v = v2; w = w2;  
    return [u2,v2,w2];  
};

Zeichnen Sie abschließend das Rechteck basierend auf den vier Festpunktkoordinaten des kleinen Rechtecks ​​

Rect.prototype.draw = function(layer){  
    this.graphics.clear();  
    this.graphics.drawVertices(1,"#000000",[this.getPoint(this.pointA),this.getPoint(this.pointB),this.getPoint(this.pointC),this.getPoint(this.pointD)],true,this.color);  
};

DrawVertices ist eine Methode der Klasse LGraphics in der Bibliothek lufylegend.js, die ein Polygon basierend auf dem eingehenden Festpunktkoordinaten-Array zeichnen kann.

Abschließend wird der vollständige Code angegeben. Es gibt nur sehr wenig Code und insgesamt 91 Zeilen JS-Code.

1. index.html

<!DOCTYPE html>  
<html>  
<head>  
<meta charset="UTF-8">  
<title>3D魔方</title>  
</head>  
<body>  
<p id="mylegend">loading……</p>  
<script type="text/javascript" src="../lufylegend-1.4.0.min.js"></script>   
<script type="text/javascript" src="./Main.js"></script>   
<script type="text/javascript" src="./Rect.js"></script>   
</body>  
</html>

2. Rect-Klasse

function Rect(pointA,pointB,pointC,pointD,angleX,angleZ,color){  
    base(this,LSprite,[]);  
    this.pointZ=[(pointA[0]+pointB[0]+pointC[0]+pointD[0])/4,(pointA[1]+pointB[1]+pointC[1]+pointD[1])/4,(pointA[2]+pointB[2]+pointC[2]+pointD[2])/4];  
    this.z = this.pointZ[2];  
    this.pointA=pointA,this.pointB=pointB,this.pointC=pointC,this.pointD=pointD,this.angleX=angleX,this.angleZ=angleZ,this.color=color;  
}  
Rect.prototype.draw = function(layer){  
    this.graphics.clear();  
    this.graphics.drawVertices(1,"#000000",[this.getPoint(this.pointA),this.getPoint(this.pointB),this.getPoint(this.pointC),this.getPoint(this.pointD)],true,this.color);  
};  
Rect.prototype.setAngle = function(a,b){  
    this.angleX = a;  
    this.angleZ = b;  
    this.z=this.getPoint(this.pointZ)[2];  
};  
Rect.prototype.getPoint = function(p){  
    var u2,v2,w2,u=p[0],v=p[1],w=p[2];  
    u2 = u * Math.cos(this.angleX) - v * Math.sin(this.angleX);  
    v2 = u * Math.sin(this.angleX) + v * Math.cos(this.angleX);  
    w2 = w;  
    u = u2; v = v2; w = w2;  
    u2 = u;  
    v2 = v * Math.cos(this.angleZ) - w * Math.sin(this.angleZ);  
    w2 = v * Math.sin(this.angleZ) + w * Math.cos(this.angleZ);  
    u = u2; v = v2; w = w2;  
    return [u2,v2,w2];  
};

Drei, Main.js

init(50,"mylegend",400,400,main);  
var a = 0,b=0,backLayer,step = 20,key = null;  
function main(){  
    backLayer = new LSprite();  
    addChild(backLayer);  
    backLayer.x = 120,backLayer.y = 120;  
    //后  
    for(var x=0;x<3;x++){  
        for(var y=0;y<3;y++){  
            z = 0;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#FF4500");  
            backLayer.addChild(rect);  
        }  
    }  
    //前  
    for(var x=0;x<3;x++){  
        for(var y=0;y<3;y++){  
            z = 3;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#FF0000");  
            backLayer.addChild(rect);  
        }  
    }  
    //上  
    for(var x=0;x<3;x++){  
        for(var z=0;z<3;z++){  
            y = 0;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-3*step + y*2*step,-step + z*2*step],0,0,"#FFFFFF");  
            backLayer.addChild(rect);  
        }  
    }  
    //下  
    for(var x=0;x<3;x++){  
        for(var z=0;z<3;z++){  
            y = 3;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-3*step + y*2*step,-step + z*2*step],0,0,"#FFFF00");  
            backLayer.addChild(rect);  
        }  
    }  
    //左  
    for(var y=0;y<3;y++){  
        for(var z=0;z<3;z++){  
            x = 0;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-3*step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#008000");  
            backLayer.addChild(rect);  
        }  
    }  
    //右  
    for(var y=0;y<3;y++){  
        for(var z=0;z<3;z++){  
            x = 3;  
            var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-3*step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#0000FF");  
            backLayer.addChild(rect);  
        }  
    }  
    backLayer.addEventListener(LEvent.ENTER_FRAME,onframe);  
}  
function onframe(){  
    a += 0.1 , b += 0.1;  
    backLayer.childList = backLayer.childList.sort(function(a,b){return a.z - b.z;});  
    for(key in backLayer.childList){  
        backLayer.childList[key].setAngle(a,b);  
        backLayer.childList[key].draw(backLayer);  
   }  
}

Ich glaube, dass Sie die Methode beherrschen, nachdem Sie den Fall in diesem Artikel gelesen haben Spannende Dinge, bitte achten Sie auf PHP Weitere verwandte Artikel auf der chinesischen Website!

Empfohlene Lektüre:

spring mvc+localResizeIMG implementiert H5-Bildkomprimierung und -Upload

Detaillierte Erläuterung der Verwendung von Canvas Zeichnungs-API

Das obige ist der detaillierte Inhalt vonH5 realisiert einen rotierenden dreidimensionalen Zauberwürfel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!