PHP-Heap implementiert Beispiel für den TopK-Algorithmus

Binärer Heap ist eine spezielle Art von Heap. Es gibt zwei Arten von binären Heaps: den Schlüsselwert des übergeordneten Heaps Knoten ist immer größer oder gleich dem Schlüsselwert eines beliebigen untergeordneten Knotens; Mindestheap: Der Schlüsselwert des übergeordneten Knotens ist immer kleiner oder gleich dem Schlüsselwert eines beliebigen untergeordneten Knotens.

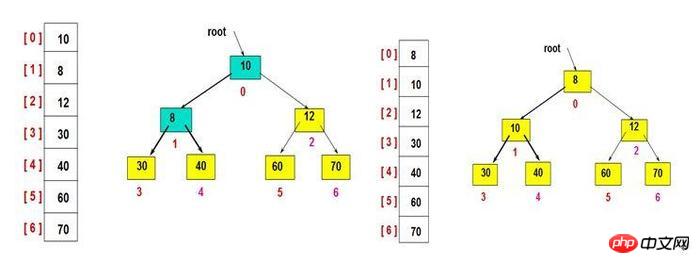
Kleiner oberer Heap – (Bild aus dem Internet)

---

Binärer Heap wird im Allgemeinen durch ein Array dargestellt (siehe Bild oben). ), Beispielsweise ist die Position des Wurzelknotens im Array 0 und die untergeordneten Knoten an der n-ten Position befinden sich an 2n+1 bzw. 2n+2. Daher befinden sich die untergeordneten Knoten an der 0-ten Position an 1 und 2 , und die untergeordneten Knoten von 1 sind bei 3 und 2n+2 4. Analog dazu erleichtert diese Speichermethode das Auffinden von übergeordneten und untergeordneten Knoten.

Ich werde hier nicht näher auf die spezifischen konzeptionellen Probleme eingehen. Wenn Sie Fragen zum binären Heap haben, können Sie diese Datenstruktur gut verstehen Um die oben genannten topN-Probleme zu implementieren und zu lösen, verwenden wir zunächst die Sortiermethode, um den Effekt zu sehen.

Verwenden Sie den Schnellsortierungsalgorithmus, um TopN zu implementieren

//为了测试运行内存调大一点ini_set('memory_limit', '2024M');//实现一个快速排序函数function quick_sort(array $array){
    $length = count($array);    $left_array = array();    $right_array = array();    if($length <= 1){        return $array;
    }    $key = $array[0];    for($i=1;$i<$length;$i++){        if($array[$i] > $key){            $right_array[] = $array[$i];
        }else{            $left_array[] = $array[$i];
        }
    }    $left_array = quick_sort($left_array);    $right_array = quick_sort($right_array);    return array_merge($right_array,array($key),$left_array);    
}//构造500w不重复数for($i=0;$i<5000000;$i++){    $numArr[] = $i; 
}//打乱它们shuffle($numArr);//现在我们从里面找到top10最大的数var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());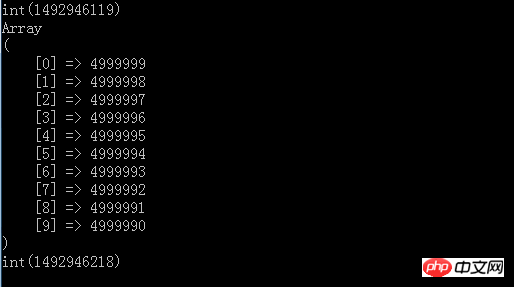

Das Ergebnis nach dem Ausführen von

---

ist OK. Ich habe oben gesehen, dass die Top10-Ergebnisse gedruckt wurden und die Laufzeit etwa 99 Sekunden beträgt. Dies ist jedoch nur der Fall, wenn 5 Millionen Zahlen in den Speicher geladen werden können oder 500 Millionen Zahlen. Es wird definitiv einige Probleme geben.

Verwenden Sie den binären Heap-Algorithmus, um TopN zu implementieren.
Der Implementierungsprozess ist:
1 Zahlen in das Array hinein, dies ist unsere topN-Nummer. Rufen Sie die Funktion zum Generieren eines kleinen oberen Heaps auf. Zu diesem Zeitpunkt muss der obere Teil des Heaps der kleinste sein 🎜>3. Durchlaufen Sie alle verbleibenden Zahlen nacheinander.
4 Vergleichen Sie die Größe jedes Mal mit dem Element oben im Heap Wenn es größer ist als das Element oben im Heap, vergleichen Sie es mit dem Element oben im Heap und rufen Sie es auf Die Funktion zum Generieren eines kleinen oberen Heaps wird verwendet, um den kleinsten Heap zu finden Innerhalb des Heaps befindet sich der größte TopN, da unser kleiner oberer Heap immer den kleinsten ausschließt und den größten belässt. Die Anpassung des kleinen oberen Heaps erfolgt ebenfalls sehr schnell. Es handelt sich nur um eine relative Anpassung, solange der Wurzelknoten vorhanden ist
7 In Bezug auf die Komplexität des Algorithmus ist es das schlimmste Szenario, dass eine Zahl, wenn sie durch den oberen Teil des Heaps ersetzt wird, angepasst werden muss Mal, was schneller ist als die Sortiergeschwindigkeit, und es werden nicht alle Inhalte in den Speicher eingelesen. Es kann verstanden werden, dass es sich bei der Leistung um eine lineare Durchquerung handelt 🎜>Nach dem Ausführen des Ergebnisses


können Sie sehen, dass das Endergebnis ebenfalls zu den Top10 gehört, aber es dauert nur etwa 1 Sekunde, und sowohl Speicher als auch Zeiteffizienz erfüllen unsere Anforderungen und sind das Beste am Sortieren Das liegt daran, dass wir nicht alle Datensätze in den Speicher einlesen müssen, da wir keine Sortierung benötigen. Das Obige dient der Demonstration, sodass 5 Millionen Elemente direkt im Speicher erstellt werden können. Wir können jedoch alle übertragen davon in die Datei übertragen und dann Zeile für Zeile lesen und vergleichen, da der Kernpunkt unserer Datenstruktur die lineare Durchquerung und der Speicher ist. Vergleichen Sie die sehr kleinen Top-Heap-Strukturen im Inneren und erhalten Sie schließlich TopN.

//生成小顶堆函数function Heap(&$arr,$idx){
    $left  = ($idx << 1) + 1;    $right = ($idx << 1) + 2;    if (!$arr[$left]){        return;
    }    if($arr[$right] && $arr[$right] < $arr[$left]){        $l = $right;
    }else{        $l = $left;
    }    if ($arr[$idx] > $arr[$l]){         $tmp = $arr[$idx]; 
         $arr[$idx] = $arr[$l];         $arr[$l] = $tmp;
         Heap($arr,$l);
    }
}//这里为了保证跟上面一致，也构造500w不重复数/*
  当然这个数据集并不一定全放在内存，也可以在
  文件里面，因为我们并不是全部加载到内存去进
  行排序
*/for($i=0;$i<5000000;$i++){    $numArr[] = $i;    
}//打乱它们shuffle($numArr);//先取出10个到数组$topArr = array_slice($numArr,0,10);//获取最后一个有子节点的索引位置//因为在构造小顶堆的时候是从最后一个有左或右节点的位置//开始从下往上不断的进行移动构造（具体可看上面的图去理解）$idx = floor(count($topArr) / 2) - 1;//生成小顶堆for($i=$idx;$i>=0;$i--){
    Heap($topArr,$i);
}

var_dump(time());//这里可以看到，就是开始遍历剩下的所有元素for($i = count($topArr); $i < count($numArr); $i++){    //每遍历一个则跟堆顶元素进行比较大小
    if ($numArr[$i] > $topArr[0]){        //如果大于堆顶元素则替换
        $topArr[0] = $numArr[$i];        /*
          重新调用生成小顶堆函数进行维护，只不过这次是从堆顶
          的索引位置开始自上往下进行维护，因为我们只是把堆顶
          的元素给替换掉了而其余的还是按照根节点小于左右节点
          的顺序摆放这也就是我们上面说的，只是相对调整下，并
          不是全部调整一遍
        */
        Heap($topArr,0);
    }
}
var_dump(time());

Ende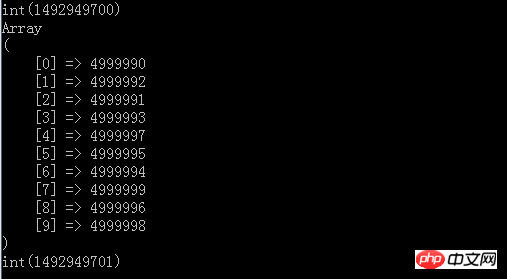

Das Letzte, was ich sagen möchte, ist
Algorithmus + Datenstruktur

Es ist wirklich sehr wichtig, ein guter Algorithmus kann unsere Effizienz erheblich verbessern.

---

Das obige ist der detaillierte Inhalt vonPHP-Heap implementiert Beispiel für den TopK-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!