So lösen Sie das Problem des Verlusts der numerischen Genauigkeit in JavaScript_Javascript-Tipps

Dieser Artikel ist in drei Teile gegliedert

• Einige typische Probleme mit dem Verlust der numerischen JS-Präzision
• Der Grund, warum die numerische Präzision von JS verloren geht
• Lösung (ein Objekt, eine Funktion)

Einige typische Probleme des digitalen Präzisionsverlusts von JS

1. Addiere zwei einfache Gleitkommazahlen

0.1 + 0.2 != 0.3 // true

Das ist wirklich kein Firebug-Problem, Sie können es mit Alert versuchen (haha, nur ein Scherz).

Sehen Sie sich die Ergebnisse der Java-Operation an

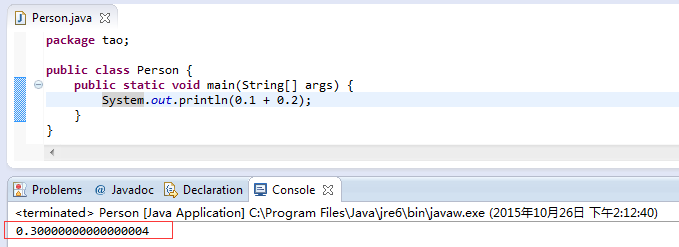
Schauen Sie sich Python noch einmal an

2. Große Ganzzahloperationen

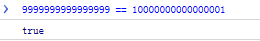
Es macht keinen Sinn, dass 16-stellige und 17-stellige Zahlen gleich sind.

Noch ein Beispiel

var x = 9007199254740992
x + 1 == x // ？

Sehen Sie sich die Ergebnisse an

Drei Ansichten wurden erneut untergraben.

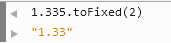
3. toFixed rundet nicht (Chrome)

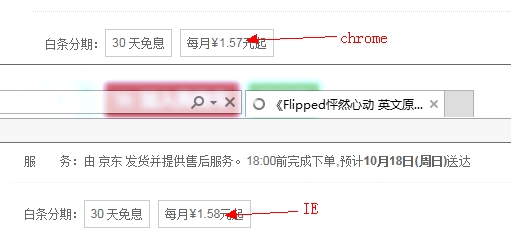
Es gab online Fälle, in denen die Preise in Chrome nicht mit denen anderer Browser übereinstimmten

2. Gründe, warum JS-Zahlen an Präzision verlieren

Die binäre Implementierung und das Bitlimit des Computers begrenzen einige Zahlen, die nicht endlich dargestellt werden können. Genauso wie einige irrationale Zahlen nicht endlich dargestellt werden können, wie zum Beispiel pi 3,1415926..., 1,3333... usw. JS folgt der Spezifikation IEEE 754, verwendet Speicher mit doppelter Genauigkeit und belegt 64 Bit. Wie im Bild gezeigt

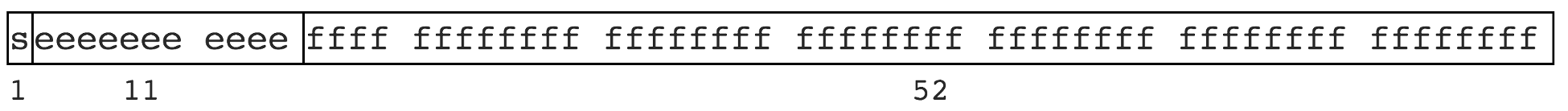
Bedeutung

• 1 Bit wird zur Darstellung des Vorzeichenbits verwendet
• 11 Bits werden zur Darstellung des Exponenten verwendet
• 52 Bit stellen die Mantisse dar

Gleitkommazahl, z. B.

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

Zu diesem Zeitpunkt können wir zum Runden nur die Dezimalzahl imitieren, aber die Binärzahl hat nur zwei Zahlen: 0 und 1, sodass sie zum Runden zu 0 und 1 wird. Dies ist die Hauptursache für Fehler und Genauigkeitsverluste bei einigen Gleitkommazahloperationen in Computern.

Der Präzisionsverlust großer Ganzzahlen ist im Wesentlichen der gleiche wie der von Gleitkommazahlen. Die maximale Anzahl von Mantissenstellen beträgt 52. Daher ist Math.pow(2, 53) die größte Ganzzahl, die in JS genau dargestellt werden kann. , was in Dezimalzahl 9007199254740992 ist.

Größere Werte als 9007199254740992 können an Präzision verlieren

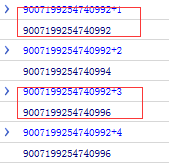
9007199254740992  >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

Eigentlich

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

Das Ergebnis ist wie im Bild dargestellt

Aus dem oben Gesagten können wir erkennen, dass die scheinbar endlichen Zahlen in der Binärdarstellung des Computers unendlich sind. Aufgrund der Begrenzung der Anzahl der Speicherstellen kommt es zu einer „Rundung“ und einem Verlust an Präzision.

3. Lösung

Bei Ganzzahlen ist die Wahrscheinlichkeit von Front-End-Problemen relativ gering. Schließlich erfordern nur wenige Geschäftsanforderungen die Verwendung sehr großer Ganzzahlen. Solange das Operationsergebnis Math.pow (2, 53) nicht überschreitet. die Genauigkeit geht nicht verloren.

Bei Dezimalzahlen besteht immer noch die Gefahr von Problemen im Frontend, insbesondere wenn einige E-Commerce-Websites Daten wie Beträge beinhalten. Lösung: Setzen Sie die Dezimalzahl in eine ganze Zahl um (multiplizieren Sie sie) und reduzieren Sie sie dann wieder auf das ursprüngliche Vielfache (multiplizieren Sie sie durch ein Vielfaches)

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

Das Folgende ist ein Objekt, das ich geschrieben habe, um den Präzisionsverlust bei dezimalen Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen zu verhindern. Natürlich darf die konvertierte Ganzzahl immer noch nicht größer als 9007199254740992 sein.

/**
 * floatObj 包含加减乘除四个方法，能确保浮点数运算不丢失精度
 *
 * 我们知道计算机编程语言里浮点数计算会存在精度丢失问题（或称舍入误差），其根本原因是二进制和实现位数限制有些数无法有限表示
 * 以下是十进制小数对应的二进制表示
 *  0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
 *  0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
 * 计算机里每种数据类型的存储是一个有限宽度，比如 JavaScript 使用 64 位存储数字类型，因此超出的会舍去。舍去的部分就是精度丢失的部分。
 *
 * ** method **
 * add / subtract / multiply /divide
 *
 * ** explame **
 * 0.1 + 0.2 == 0.30000000000000004 （多了 0.00000000000004）
 * 0.2 + 0.4 == 0.6000000000000001 （多了 0.0000000000001）
 * 19.9 * 100 == 1989.9999999999998 （少了 0.0000000000002）
 *
 * floatObj.add(0.1, 0.2) >> 0.3
 * floatObj.multiply(19.9, 100) >> 1990
 *
 */
var floatObj = function() {
 
 /*
  * 判断obj是否为一个整数
  */
 function isInteger(obj) {
  return Math.floor(obj) === obj
 }
 
 /*
  * 将一个浮点数转成整数，返回整数和倍数。如 3.14 >> 314，倍数是 100
  * @param floatNum {number} 小数
  * @return {object}
  * {times:100, num: 314}
  */
 function toInteger(floatNum) {
  var ret = {times: 0, num: 0}
  if (isInteger(floatNum)) {
   ret.num = floatNum
   return ret
  }
  var strfi = floatNum + ''
  var dotPos = strfi.indexOf('.')
  var len = strfi.substr(dotPos+1).length
  var times = Math.pow(10, len)
  var intNum = parseInt(floatNum * times + 0.5, 10)
  ret.times = times
  ret.num = intNum
  return ret
 }
 
 /*
  * 核心方法，实现加减乘除运算，确保不丢失精度
  * 思路：把小数放大为整数（乘），进行算术运算，再缩小为小数（除）
  *
  * @param a {number} 运算数1
  * @param b {number} 运算数2
  * @param digits {number} 精度，保留的小数点数，比如 2, 即保留为两位小数
  * @param op {string} 运算类型，有加减乘除（add/subtract/multiply/divide）
  *
  */
 function operation(a, b, digits, op) {
  var o1 = toInteger(a)
  var o2 = toInteger(b)
  var max = o1.times > o2.times ? o1.times : o2.times
  var result = null
  switch (op) {
   case 'add':
    result = o1.num + o2.num
    break
   case 'subtract':
    result = o1.num - o2.num
    break
   case 'multiply':
    result = o1.num * o2.num
    break
   case 'divide':
    result = o1.num / o2.num
    break
  }
  return result / max
 }
 
 // 加减乘除的四个接口
 function add(a, b, digits) {
  return operation(a, b, digits, 'add')
 }
 function subtract(a, b, digits) {
  return operation(a, b, digits, 'subtract')
 }
 function multiply(a, b, digits) {
  return operation(a, b, digits, 'multiply')
 }
 function divide(a, b, digits) {
  return operation(a, b, digits, 'divide')
 }
 
 // exports
 return {
  add: add,
  subtract: subtract,
  multiply: multiply,
  divide: divide
 }
 
}();

ToFixed wird wie folgt behoben

// toFixed 修复
function toFixed(num, s) {
 var times = Math.pow(10, s)
 var des = num * times + 0.5
 des = parseInt(des, 10) / times
 return des + ''
}

Das Obige befasst sich mit dem Problem des numerischen Präzisionsverlusts in JavaScript. Es analysiert typische Probleme, analysiert die Gründe für den numerischen Präzisionsverlust und teilt auch Lösungen mit. Ich hoffe, dass es für das Lernen aller hilfreich ist.