Teilen Sie Tipps zur parabolischen Bewegung von Bildern in HTML5

Dieser Artikel stellt hauptsächlich einige Gedanken zur parabolischen Bewegung von Bildern in h5 vor und stellt die Bewegungsmethode entlang der Bezier-Kurve detailliert vor. Ich hoffe, dass er allen helfen kann .

Üblicherweise ist das Bewegen von Objekten/Bildern in einer Parabel oder genauer gesagt entlang einer Bezier-Kurve eine häufige Anforderung in der H5-Entwicklung. Daher ist die schnelle Berechnung des Bewegungspfads auf der Grundlage des Designentwurfs die erste Lösung Entwickler.

Die hier häufig verwendete Designentwurfsgröße für die H5-Entwicklung ist 640 * 1008, daher lautet die Lösungsidee basierend auf dieser Größe wie folgt:

1 Zu verschiebende Elemente in PS Exportieren Sie eine PNG-Datei. Wenn die Bewegungsroute im Entwurfsentwurf geplant wurde, müssen Sie die Route auch als PNG exportieren als Entwurfsentwurf und fügen Sie dann die Verschiebungselemente hinzu. Ziehen Sie sie zweimal in die Datei. Wenn eine Bewegungsroute vorhanden ist, ziehen Sie sie ebenfalls hinein, wie unten gezeigt:

Was Hier ist auf die Platzierung des Verschiebungsbildes zu achten. Der Startpunkt und der Endpunkt des Pfades sollten dem Bewegungspunkt des Bildes entsprechen. Die entsprechenden Situationen sind wie folgt:

Es gibt keine Verformungsverarbeitung in der Leinwand, dann ist der Bewegungspunkt die obere linke Ecke des Bildes
In der Leinwand wurde das Bild übersetzt und verschoben, weil drawImage (image, sx, sy, sWidth, sHeight, dx, dy wird entsprechend x1, y1 in translator(x1, y1) , dWidth, dHeight hinzugefügt) der endgültige Versatz von dx und dy.
Wenn das Element durch position:absolute positioniert wird und die Position durch translator3d(x, y, z) in transform gesteuert wird, sollte der Offset x, y sein. Normalerweise können wir in transform links, oben und zusätzlich imitieren margin, um die Position des Elements zu steuern und ein zusätzliches Translate3D(marginLeftX, marginLeftY, 0) in transform hinzuzufügen. Berücksichtigen Sie auch den Wert dieses Margin AI, verwenden Sie die Tasten Strg + R, um die Referenzlinie herauszuziehen, und verschieben Sie das Elementbild, um seine x- und y-Position wie folgt herauszuziehen. Wie im Bild gezeigt:

Wählen Sie dann das Stiftwerkzeug aus, klicken Sie nacheinander auf den Startpunkt und den Endpunkt, lassen Sie die Maus nicht los, nachdem Sie auf den Endpunkt geklickt haben, ziehen Sie die KI direkt und es werden automatisch 2 Kontrollpunkte hinzugefügt. Sie können die Position anpassen der beiden Kontrollpunkte, indem Sie die Maus bewegen, um den vom Stiftwerkzeug generierten Pfad anzupassen, bis er mit dem Referenzlinienpfad im Entwurfsentwurf übereinstimmt:

Lassen Sie nach dem Ziehen an die gewünschte Position die Maustaste los und drücken Sie die Eingabetaste, um den Pfad zu bestätigen. Wenn der umrissene Pfad nicht Ihren Wünschen entspricht, können Sie die Kontrollpunkte weiter ziehen, um Anpassungen vorzunehmen.

4 , danach Wenn die Anpassung abgeschlossen ist, ziehen Sie zwei zusätzliche Referenzlinien an die Position von Kontrollpunkt 1, öffnen Sie dann das Informationsfeld über die Menüleiste – Fenster – Informationen und legen Sie den Startpunkt, den Kontrollpunkt, den Endpunkt und die Koordinaten der drei fest Nehmen Sie es heraus.

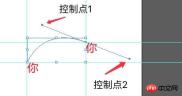5, berechnen Sie die Pixeldifferenz zwischen Kontrollpunkt, Endpunkt und Startpunkt und berechnen Sie den tatsächlichen Kontrollpunkt basierend auf den tatsächlichen x-, y-Koordinatenwerten und Pixeln Differenz des zu verschiebenden Bildes in H5. Wenden Sie dann diese drei Koordinatenpunkte auf die Formel an

Der Code lautet wie folgt:

var path = getBezierPath([278 + 119, 572 - 32], [ 278 - 4, 572 - 137] , [ 278 + 119, 572 - 32] , [ 278, 572], 50);

Darunter sind die Parameter getBezierPath (Endpunkt, Kontrollpunkt 1, Kontrollpunkt 2, Startpunkt, Nummer Wenn es keinen Kontrollpunkt 2 gibt, geben Sie einfach die Koordinaten ein. Die endgültige Formel von _getBezierPath lautet wie folgt:

Verwandte Empfehlungen:

Zwei JS-Implementierungen kleiner Kugeln Parabolische Flugbahnbewegungsmethode

Codebeispiel für eine Animation elastischer potentieller Energie in JavaScript über Parabel Bewegung

jQuery-Implementierungsmethode für parabolische Bewegungen (vollständige Demo im Anhang) Quellcode-Download)_jquery

function getBezierPath(p1, p2, p3, p4, times) {
    function Point2D(x,y){  
        this.x = x || 0.0;  
        this.y = y ||0.0;  
    }  
    
    function PointOnCubicBezier( cp, t ) {  
        var   ax, bx, cx;  
        var   ay, by, cy;  
        var   tSquared, tCubed;  
        var   result = new Point2D ;  
        cx = 3.0 * (cp[1].x - cp[0].x);  
        bx = 3.0 * (cp[2].x - cp[1].x) - cx;  
        ax = cp[3].x - cp[0].x - cx - bx;        
        cy = 3.0 * (cp[1].y - cp[0].y);  
        by = 3.0 * (cp[2].y - cp[1].y) - cy;  
        ay = cp[3].y - cp[0].y - cy - by;        
        tSquared = t * t;  
        tCubed = tSquared * t;        
        result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;  
        result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;        
        return result;  
    }  
    function ComputeBezier( cp, numberOfPoints, curve ){  
        var   dt;  
        var   i;        
        dt = 1.0 / ( numberOfPoints - 1 );  
         for( i = 0; i < numberOfPoints; i++)  
            curve[i] = PointOnCubicBezier( cp, i*dt );  
    }  
      
    var cp=[  
        new Point2D(parseInt(p4[0]), parseInt(p4[1])), new Point2D(p2[0], p2[1]), new Point2D(p3[0], p3[1]), new Point2D(p1[0], p1[1])  
    ];  
    var numberOfPoints = times;  
    var curve=[];  
    ComputeBezier( cp, numberOfPoints, curve );  
    return curve;
}

Das obige ist der detaillierte Inhalt vonTeilen Sie Tipps zur parabolischen Bewegung von Bildern in HTML5. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!