Heim >Web-Frontend >js-Tutorial >Detaillierte Erläuterung der Blasensortiermethode
Detaillierte Erläuterung der Blasensortiermethode
- 一个新手Original
- 2017-10-06 10:41:442929Durchsuche
Blasensortiermethode
HTML5 Academy-Coder: In dieser Ausgabe wird weiterhin der Algorithmus vorgestellt – die Blasensortiermethode. Der Blasensortierungsalgorithmus ist relativ einfach, leicht zu verwenden und relativ stabil. Er ist ein relativ leicht verständlicher Algorithmus und einer der Algorithmen, zu denen Interviewer häufig Fragen stellen.
Tipps: Die Grundkenntnisse zu „Algorithmus“ und „Sortierung“ wurden im vorherigen Abschnitt „Auswahlsortiermethode“ ausführlich erläutert. Sie können auf den entsprechenden Artikellink am Ende des Artikels klicken, um ihn anzuzeigen , und ich werde es hier nicht wiederholen.
Prinzip der Blasensortierung
Grundprinzip
Traverse vom Kopf der Sequenz aus, vergleiche sie paarweise, wenn ersteres größer als letzteres ist, tausche die Positionen bis das Ende Vertauschen Sie die größte Zahl (die größte Zahl in dieser Sortierung) mit dem Ende der ungeordneten Sequenz und werden Sie dadurch Teil der geordneten Sequenz.
Während des nächsten Durchlaufs wird die maximale Zahl nach jedem vorherigen Durchlauf nein länger teilnehmen Sortieren;
Wiederholen Sie diesen Vorgang mehrmals, bis die Sequenz sortiert ist.
Da beim Sortiervorgang Dezimalstellen immer nach vorne und große Zahlen nach hinten gestellt werden, ähnlich wie Blasen, die allmählich nach oben schweben, spricht man von Blasensortierung.
Prinzipdiagramm
Tipps: Blau steht für das Warten auf den Austausch in einer Sortierrunde, Schwarz für den in dieser Sortierrunde abgeschlossenen Austausch, Rot für den abgeschlossenen Sortiervorgang
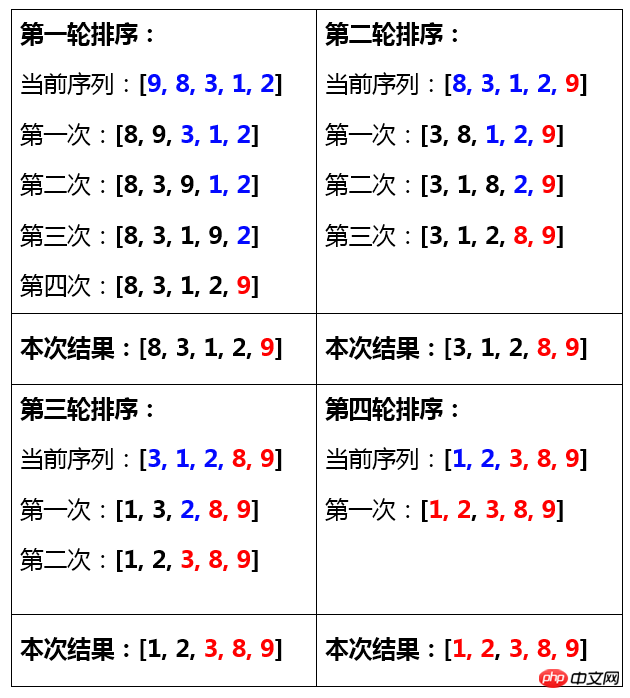
Blasenschrittzerlegung erreichen
Verwenden Sie eine for-Schleife, um die Anzahl der Sortierungen zu bestimmen
Da die Reihenfolge bereits bestimmt werden kann, wenn nur noch eine Zahl in der Reihenfolge übrig ist Sortiert werden muss, ist keine Sortierung erforderlich, daher ist die Anzahl der Sortierreihenfolgelängen 1.

Kontrollieren Sie die Anzahl der Vergleiche für jede Sortierung.
Bei jeder Sortierung müssen mehrere Zahlen in der Reihenfolge paarweise verglichen werden. Es sind mehrere Vergleiche erforderlich. Verwenden Sie die for-Anweisung, um dies zu erreichen. Diese for-Schleife ist in der for-Schleife der sortierten Zeiten verschachtelt (und bildet ein Nest aus doppelten for).

Tipps: j muss auf weniger als len - i - 1 eingestellt werden. Der Grund für die Subtraktion von i ist, dass die sortierten Zahlen nicht mehr in den Vergleich einbezogen werden Der Grund für die Subtraktion von 1 ist, dass das Array unter Indexwerten liegt, die bei 0 beginnen.
Kernfunktion - Paare vergleichen und Positionen entsprechend der Situation austauschen
Vergleichen Sie die Größe zweier Zahlen als die letztere, tauschen Sie die Werte aus, d. h. tauschen Sie die Positionen aus .

Vollständiger Code der Blasensortierung

Optimierung der Blasensortierung
Wenn die Sequenz Die Daten ist: [0, 1, 2, 3, 4, 5];
verwendet zum Sortieren die obige Blasensortiermethode, und das erhaltene Ergebnis ist definitiv kein Problem, aber die zu sortierende Reihenfolge ist in Ordnung Theoretisch besteht keine Notwendigkeit, die Sortierung zu durchlaufen.
Der aktuelle Algorithmus führt die Durchlaufsortierung unabhängig davon durch, ob die Anfangssequenz in Ordnung ist, und die Effizienz ist relativ gering, sodass der aktuelle Sortieralgorithmus optimiert werden muss.
Im folgenden Algorithmus wird eine Swap-Variable eingeführt und vor jeder Sortierung auf „false“ initialisiert. Wenn zwei Zahlen ihre Positionen tauschen, wird sie auf „true“ gesetzt.
Am Ende jeder Sortierung wird beurteilt, ob der Austausch falsch ist. Wenn dies der Fall ist, bedeutet dies, dass die Sequenz sortiert wurde oder die Sequenz selbst eine geordnete Sequenz ist und die nächste Sortierung nicht durchgeführt wird .
Durch diese Methode werden unnötige Vergleiche und Positionsaustausche reduziert, was die Leistung des Algorithmus weiter verbessert.

Effizienz der Blasensortiermethode
Zeitkomplexität
Bester Zustand: Die zu sortierende Sequenz selbst ist eine geordnete Sequenz Aus dem optimierten Code kann geschlossen werden, dass die Anzahl der Sortierungen n-1 beträgt und die Zeitkomplexität O(n) beträgt. Schlimmster Fall: Die zu sortierende Reihenfolge ist in umgekehrter Reihenfolge und 1 muss zu diesem Zeitpunkt sortiert werden + 2 +3…(n - 1) = n(n – 1)/2 mal
Die Zeitkomplexität ist O(n^2).
Raumkomplexität
Die Blasensortiermethode erfordert einen zusätzlichen Raum (temporäre Variable), um die Position von Elementen auszutauschen, sodass die Raumkomplexität O(1) ist.
Stabilität des Algorithmus
Wenn benachbarte Elemente gleich sind, besteht keine Notwendigkeit, die Positionen zu tauschen, und die Reihenfolge derselben Elemente ändert sich nicht. Daher handelt es sich um eine stabile Sortierung.
Was ist O? !
Zeitkomplexität beschreibt genauer gesagt die zeitliche Wachstumskurve eines Algorithmus, wenn die Größe des Problems weiter zunimmt. Daher stellen diese Steigerungen um Größenordnungen keine genaue Leistungsbewertung dar und können als Näherungswert verstanden werden. (Ähnlich der räumlichen Komplexität)
O(n?) bedeutet, dass die Komplexität ungefähr gleich Cn? ist, wenn n groß genug ist. Einfach ausgedrückt, wenn n groß genug ist n wächst linear, die Komplexität wächst quadratisch.
O(n) bedeutet, dass, wenn n sehr groß ist, die Komplexität ungefähr gleich Cn ist und C eine bestimmte Konstante ist. Kurz gesagt: Wenn n linear wächst, wächst die Komplexität linear.
O(1) bedeutet, dass die Komplexität grundsätzlich nicht zunimmt, wenn n sehr groß ist. Kurz gesagt: Da n linear wächst, wird die Komplexität nicht von n beeinflusst und wächst entlang eines konstanten Niveaus (die Konstante ist hier 1).
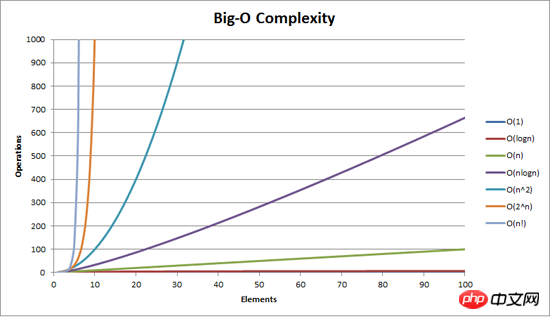
Tipps: Im Bild liegt O(1) nahe der X-Achse und ist nicht deutlich zu sehen.
Tipps: Dieses Bild stammt von der Website „Stack Overflow“.
Links zu verwandten Artikeln
Sortiermethode auswählen
Sei jeden Tag glücklich
Das Leben ist hart und Programmieren ist nicht einfach, aber vergessen Sie es nicht lächeln!

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Blasensortiermethode. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

