Heim >Java >javaLernprogramm >Detaillierte Erläuterung von Methodenbeispielen zur Implementierung des Merge-Sort-Algorithmus in Java
Detaillierte Erläuterung von Methodenbeispielen zur Implementierung des Merge-Sort-Algorithmus in Java
- 黄舟Original
- 2017-09-23 09:58:222092Durchsuche
In diesem Artikel werden hauptsächlich relevante Informationen zur detaillierten Erläuterung des Zusammenführungssortierungsalgorithmus in Java vorgestellt. Es handelt sich also um einen Sortieralgorithmus mit einer Zeitkomplexität von O(N logN). Es wird im täglichen Leben häufig verwendet. Freunde, die es benötigen, können sich auf
Detaillierte Erklärung des Zusammenführungssortierungsalgorithmus in Java beziehen Der Sortieralgorithmus ist, wie der Name schon sagt, eine Methode, die zuerst den Algorithmus teilt und dann kombiniert. Die Idee des Algorithmus besteht darin, das zu sortierende Array in einzelne Elemente zu zerlegen, wobei jedes Element ein einzelnes Individuum ist, und dann die beiden benachbarten Elemente von klein auf zu sortieren zu groß oder von groß nach klein, um ein Ganzes zu bilden, und dann wird jedes Ganze mit einem bestimmten Algorithmus zusammengeführt Das Ganze enthält drei Elemente. Fahren Sie mit dem Zusammenführen benachbarter Ganzen fort, bis alle Ganzen zu einem Ganzen zusammengeführt sind. Das endgültige Ganze ist das Ergebnis der Sortierung des ursprünglichen Arrays.
Bei benachbarten Ganzen besteht die Idee des Zusammenführens darin, das kleinste Element der beiden Ganzen zu nehmen (vorausgesetzt, sie sind tatsächlich in aufsteigender Reihenfolge sortiert) und es jedes Mal in ein neues Array einzufügen Durchlaufen Sie es und schließlich die beiden Ganzen. Nachdem alle Elemente aufgenommen wurden, wird ein in aufsteigender Reihenfolge sortiertes Ganzes erhalten. Der Zusammenführungsprozess ähnelt zwei aufsteigend geordneten Decks A und B (wie in der Abbildung gezeigt). Jedes Mal wird ein Element von oben genommen und in Deck C platziert: Aus dem Bild ist ersichtlich, dass für zwei benachbarte Ganzheiten A und B die darin enthaltenen Elemente in aufsteigender Reihenfolge sortiert sind. Jetzt gibt es ein temporäres Array C und dann die beiden Elemente oben in A und B. Nehmen Sie das kleinere Element heraus und fügen Sie es in C ein. Für das gesamte herausgenommene Element verschieben Sie den Index, der auf das Element zeigt, um ein Bit nach unten. Nehmen Sie weiterhin das kleinere der oberen Elemente der beiden Ganzen heraus und fügen Sie es in C ein. und Schleife nacheinander: Wenn die Elemente eines bestimmten Ganzen abgerufen werden, werden alle Elemente des anderen Ganzen direkt in C verschoben. Für das ganze C wird es durch Sortieren von A und B erhalten. Da A und B zwei benachbarte Ganzen sind, müssen Sie am Ende nur die Elemente in C in ein gemeinsames Ganzes kopieren, das aus A und B besteht. Das ist jedoch Dadurch wird auch der Zweck erreicht, A und B zusammenzuführen und gleichzeitig zu sortieren. 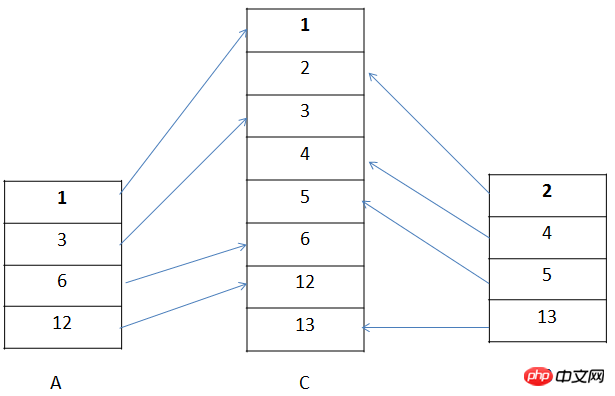
Der Code enthält zwei Hauptmethoden
public class MergeSort {
public static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr) {
AnyType[] tmp = ((AnyType[]) new Comparable[arr.length]);
mergeSort(arr, 0, arr.length - 1, tmp);
}
private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr, int start, int end, AnyType[] tmp) {
if (start < end) {
int mid = (start + end) >> 1;
mergeSort(arr, start, mid, tmp);
mergeSort(arr, mid + 1, end, tmp);
merge(arr, start, mid, end, tmp);
}
}
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] arr, int start, int mid, int end, AnyType[] tmp) {
int i = start, j = mid + 1, k = start;
while (i <= mid && j <= end) {
if (arr[i].compareTo(arr[j]) < 0) {
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= end) {
tmp[k++] = arr[j++];
}
for (int m = start; m <= end; m++) {
arr[m] = tmp[m];
}
}
}
private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] arr, int start, int end, AnyType[] tmp)
Die erste Methode ist eine rekursive Methode
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] arr, int start, int mid, int end, AnyType[] tmp)
Die Funktion der zweiten Methode besteht darin, die beiden sortierten Teile zusammenzuführen Bei der ersten Methode besteht der letzte Schritt darin, die zweite Methode auszuführen, die darin besteht, die beiden vorherigen Schritte zu sortieren. Nach dem Zusammenführen der Teile ist die Funktion dieser Methode abgeschlossen. Was die zweite Methode betrifft, ist die Implementierungsidee die gleiche wie zuvor beschrieben. Nehmen Sie das kleinere Element vom oberen der beiden Kartenstapel und legen Sie es in eine temporäre Anordnung. Wenn ein Kartenstapel herausgenommen wird, legen Sie die restlichen Elemente ab des Arrays in Das zweite Deck fügt schließlich die Elemente des temporären Arrays wieder in das ursprüngliche Array ein.
In diesem Artikel wird hauptsächlich die Idee der Zusammenführungssortierung ausführlich erläutert und der Code anhand spezifischer Codes und Ideen analysiert.
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung von Methodenbeispielen zur Implementierung des Merge-Sort-Algorithmus in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

