js implementiert Datenstrukturen: Baum und Binärbaum, Binärbaumdurchquerung und grundlegende Operationsmethoden

Baumstruktur ist eine sehr wichtige Art nichtlinearer Struktur. Intuitiv ist eine Baumstruktur eine hierarchische Struktur, die durch Verzweigungsbeziehungen definiert wird.

Bäume werden auch häufig im Computerbereich verwendet. In Compilern werden Bäume beispielsweise zur Darstellung der grammatikalischen Struktur des Quellprogramms verwendet Verhalten von Algorithmen, Bäume können verwendet werden, um seinen Ausführungsprozess usw. zu beschreiben.

Schauen wir uns zunächst einige Konzepte von Bäumen an: 1. Baum (Baum) ist eine endliche Menge von n (n>=0) Knoten. In jedem nicht leeren Baum:

(1) Es gibt und gibt nur einen bestimmten Knoten namens Wurzel

(2) Wenn n>1, können die verbleibenden Knoten in m ( m>0) gegenseitig disjunkte endliche Mengen T1, T2, T3,...Tm, von denen jede selbst ein Baum ist und Teilbaum der Wurzel genannt wird.

Zum Beispiel ist (a) ein Baum mit nur einem Wurzelknoten; (b) ist ein Baum mit 13 Knoten, wobei A die Wurzel ist und die übrigen Knoten in 3 disjunkte Teilmengen unterteilt sind: T1= {B,E,F,K,L},t2={D,H,I,J,M};T1, T2 und T3 sind alle Teilbäume der Wurzel A und selbst ein Baum.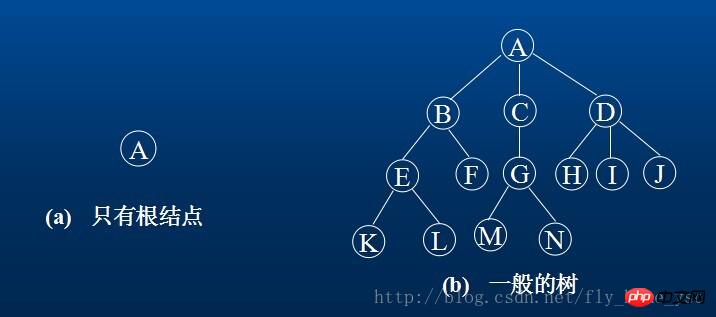

2. Der Knoten des Baums enthält ein Datenelement und mehrere Zweige, die auf seine Unterbäume verweisen. Die Anzahl der Teilbäume, die ein Knoten hat, wird als Grad des Knotens bezeichnet. In (b) ist beispielsweise der Grad von A 3, der Grad von C 1 und der Grad von F 0. Der Knoten mit Grad 0 wird Blatt- oder Endknoten genannt. Knoten mit einem anderen Grad als 0 werden als nichtterminale Knoten oder Verzweigungsknoten bezeichnet. Der Grad eines Baums ist der maximale Grad jedes Knotens im Baum. Der Grad des Baums in (b) ist 3. Die Wurzel des Teilbaums eines Knotens wird als Kind des Knotens bezeichnet. Dementsprechend wird dieser Knoten als übergeordneter Knoten des Kindes bezeichnet. Kinder derselben Eltern nennen sich gegenseitig Geschwister. Die Vorfahren eines Knotens sind alle Knoten auf den Zweigen von der Wurzel bis zum Knoten. Im Gegensatz dazu wird jeder Knoten im Teilbaum, der an einem Knoten wurzelt, als Nachkomme dieses Knotens bezeichnet.

3. Die Ebene eines Knotens wird ausgehend von der Wurzel definiert. Die Wurzel ist die erste Ebene und die folgenden untergeordneten Elemente sind die zweite Ebene. Wenn sich ein Knoten auf der Ebene l befindet, befindet sich die Wurzel seines Teilbaums auf der Ebene l+1. Die Knoten, deren Eltern auf derselben Ebene liegen, sind Cousins ​​voneinander. Beispielsweise sind die Knoten G und E, F, H, I und J Cousins ​​voneinander. Die maximale Knotenebene im Baum wird als Tiefe oder Höhe des Baums bezeichnet. Die Tiefe des Baums in (b) beträgt 4.

4. Wenn die Teilbäume der Knoten im Baum als von links nach rechts geordnet betrachtet werden (d. h. sie können nicht ausgetauscht werden), wird der Baum als geordneter Baum bezeichnet, andernfalls wird er als ungeordneter Baum bezeichnet Baum. In einem geordneten Baum wird die Wurzel des Teilbaums ganz links als erstes Kind bezeichnet, und die Wurzel des Teilbaums ganz rechts wird als letztes Kind bezeichnet.

5. Wald ist eine Sammlung von m (m>=0) disjunkten Bäumen. Für jeden Knoten im Baum ist die Menge seiner Teilbäume der Wald.

Werfen wir einen Blick auf Konzepte im Zusammenhang mit Binärbäumen:

Binärbaum ist eine weitere Baumstruktur. Sein Merkmal ist, dass jeder Knoten höchstens zwei Unterbäume hat (d. h. es gibt keine). Knoten mit Grad größer als 2) und die Teilbäume eines Binärbaums können in linke und rechte Teilbäume unterteilt werden (die Reihenfolge kann nicht beliebig umgekehrt werden).

Eigenschaften von Binärbäumen:

1 . Im Binärbaum gibt es höchstens 2 i-1 Leistungsknoten auf der i-ten Schicht (i>=1).

2. Ein Binärbaum mit Tiefe k hat höchstens 2 k-1 Knoten (k>=1).

　3. Wenn für jeden Binärbaum T die Anzahl der Endknoten n0 und die Anzahl der Knoten mit Grad 2 n2 ist, dann ist n0 = n2 + 1;

　Die Tiefe des Der Baum ist k. Ein Binärbaum mit 2 k-1 Knoten wird als vollständiger Binärbaum bezeichnet.

Ein Binärbaum mit n Knoten der Tiefe k, genau dann, wenn jeder seiner Knoten den Knoten mit den Nummern 1 bis n im vollständigen Binärbaum der Tiefe k entspricht. Er wird als vollständiger Binärbaum bezeichnet.

Das Folgende sind zwei Merkmale eines vollständigen Binärbaums:

4. Die Tiefe eines vollständigen Binärbaums mit n Knoten beträgt Math.floor(log 2 n) + 1

5. Wenn die Knoten eines vollständigen Binärbaums mit n Knoten (seine Tiefe ist Math.floor(log 2 n) + 1) in Schichtenreihenfolge nummeriert werden (von der 1. Ebene bis zum Math.floor(2 n) + 1, jede Ebene von links nach rechts), dann für jeden Knoten (1

　(1) Wenn i=1, dann ist Knoten i eine binäre Baumwurzel, keine Eltern; Wenn i>1, dann ist sein übergeordneter Knoten (i) der Knoten Math.floor(i/2).

　(2) Wenn 2i > n, dann hat Knoten i kein linkes Kind (Knoten i ist ein Blattknoten); andernfalls ist sein linkes Kind LChild(i) Knoten 2i.

　　(3) Wenn 2i + 1 > n, dann hat Knoten i kein rechtes Kind; andernfalls ist sein rechtes Kind Knoten 2i + 1; 🎜>
Speicherstruktur des Binärbaums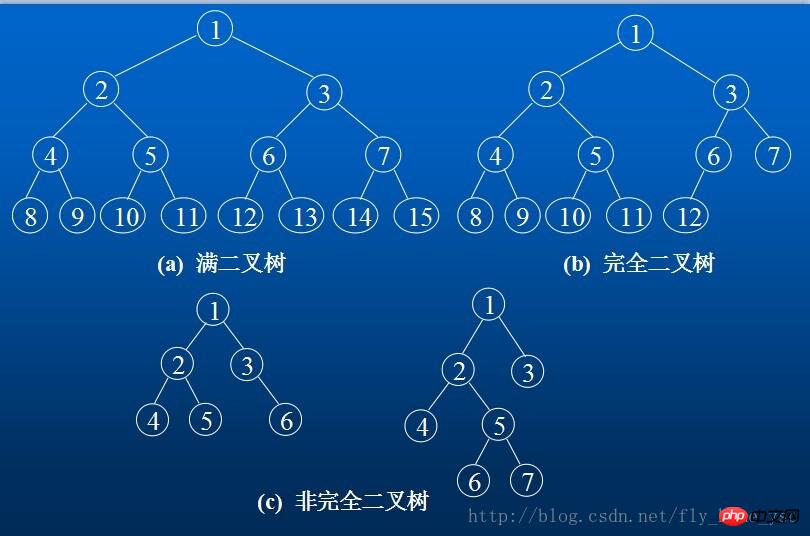

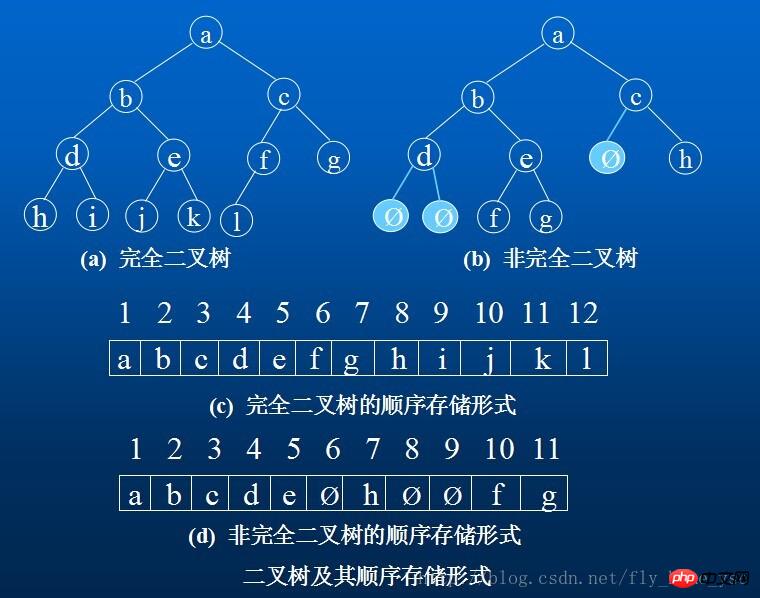
1. Sequentielle Speicherstruktur
Verwenden Sie einen Satz kontinuierlicher Speichereinheiten, um die Knotenelemente im gesamten Binärbaum von oben nach unten und von links nach rechts zu speichern, dh das Knotenelement mit der Nummer i im Binärbaum wird in der Komponente mit dem Index i-1 im oben definierten eindimensionalen Array gespeichert. „0“ zeigt an, dass dieser Knoten nicht existiert. Diese sequentielle Speicherstruktur ist nur für vollständige Binärbäume geeignet.
Denn im schlimmsten Fall erfordert ein einzweigiger Baum mit der Tiefe k und nur k Knoten (es gibt keinen Knoten mit Grad 2 im Baum) eine Länge von 2 hoch -1 dimensionales Array.

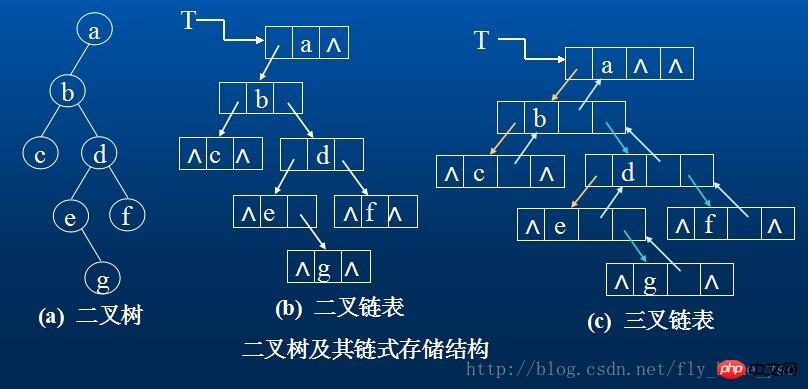
2. Verknüpfte Speicherstruktur
Der Knoten eines Binärbaums besteht aus einem Datenelement und zwei Zweigen, die auf seinen linken bzw. rechten Teilbaum zeigen, was bedeutet, dass die Knoten in der verknüpften Liste des Binärbaums sind mindestens drei Felder enthalten: Datenfeld sowie linke und rechte Zeigerfelder. Um das Auffinden der übergeordneten Knoten eines Knotens zu erleichtern, kann der Knotenstruktur manchmal ein Zeigerfeld hinzugefügt werden, das auf den übergeordneten Knoten zeigt. Die durch Verwendung dieser beiden Strukturen erhaltenen Speicherstrukturen von Binärbäumen werden als binär verknüpfte Listen bzw. dreifach verknüpfte Listen bezeichnet.
Es gibt n+1 leere Linkfelder in einer binär verknüpften Liste mit n Knoten. Wir können diese leeren Linkfelder verwenden, um andere nützliche Informationen zu speichern und so eine andere verknüpfte Speicherstruktur zu erhalten – eine verknüpfte Hinweisliste.

Es gibt drei Haupttypen der Binärbaumdurchquerung:

Durchquerung erster Ordnung (Wurzel): Wurzel links und rechts
Durchquerung mittlerer Ordnung (Wurzel): Linke Wurzel rechts
Zurück (Wurzel-)Reihenfolge Durchquerung: Linke und rechte Wurzeln

Sequentielle Speicherstruktur des Binärbaums:

Verkettete Speicherform des Binärbaums:

// 顺序存储结构
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];
    // 链式存储结构
    function BinaryTree(data, leftChild, rightChild) {
        this.data = data || null;
        // 左右孩子结点
        this.leftChild = leftChild || null;
        this.rightChild = rightChild || null;
    }

Durchqueren des Binärbaums: bezieht sich auf den einmaligen Besuch jedes Knotens im Binärbaum gemäß einer festgelegten Regel.

1. Vorbestellungsdurchlauf des Binärbaums

1) Die rekursive Definition des Algorithmus lautet:

Wenn der Binärbaum leer ist, endet der Durchlauf

　⑴ Besuchen Sie den Wurzelknoten;

　⑵ Durchlaufen Sie den linken Teilbaum der Reihe nach (rufen Sie diesen Algorithmus rekursiv auf);

　⑶ Durchlaufen Sie den rechten Teilbaum der Reihe nach (rufen Sie diesen Algorithmus rekursiv auf) .

Algorithmusimplementierung:

// 顺序存储结构的递归先序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    console.log('preOrder:');
    void function preOrderTraverse(x, visit) {
        visit(tree[x]);
        if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储结构的递归先序遍历
    BinaryTree.prototype.preOrderTraverse = function preOrderTraverse(visit) {
        visit(this.data);
        if (this.leftChild) preOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) preOrderTraverse.call(this.rightChild, visit);
    };

2) Nicht rekursiver Algorithmus:

Angenommen, T ist eine Variable, die auf den Wurzelknoten des Binärbaums zeigt, den nicht rekursiven Algorithmus ist: Wenn der Binärbaum leer ist, dann sei p=T; (1) p ist der Wurzelknoten

(2) Wenn p nicht leer ist oder der Stapel ist nicht leer;

(3) Wenn p nicht leer ist, greifen Sie auf den durch p gezeigten Knoten zu, schieben Sie p auf den Stapel, p = p.leftChild, greifen Sie auf den linken Teilbaum zu; > (4) Ansonsten; gehe zurück zu p, dann p = p.rightChild, greife auf den rechten Teilbaum zu

　(5) Gehe zu (2), bis der Stapel leer ist.

Code-Implementierung:

2. Durchlauf des Binärbaums in der richtigen Reihenfolge:

1) Die rekursive Definition des Algorithmus lautet:

// 链式存储的非递归先序遍历

    // 方法1
    BinaryTree.prototype.preOrder_stack = function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {
                p.data && visit(p.data);                
                stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();                
                stack.push(p.rightChild);
            }
        }
    };    // 方法2
     BinaryTree.prototype.preOrder_stack2 = function (visit) {        
     var stack = new Stack();        
     var p = this;        
     while (p || stack.top) {            
     if (p) {                
     stack.push(p);
                p.data && visit(p.data);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p = p.rightChild;
            }
        }
    };

Wenn der Binärbaum leer ist, endet die Durchquerung; andernfalls

　⑴ Durchlaufen Sie den linken Teilbaum (rufen Sie diesen Algorithmus rekursiv auf);

　⑵ Besuchen Sie den Wurzelknoten;

　⑶ Der rechte Teilbaum der Reihe nach durchlaufen (diesen Algorithmus rekursiv aufrufen).

2) Nicht-rekursiver Algorithmus

T ist eine Variable, die auf den Wurzelknoten des Binärbaums zeigt. Der nicht-rekursive Algorithmus lautet: Wenn der Binärbaum leer ist, kehre zurück ; andernfalls sei p=T

// 顺序存储结构的递归中序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('inOrder:');
    void function inOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
        visit(tree[x]);
        if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });

    // 链式存储的递归中序遍历
    BinaryTree.prototype.inPrderTraverse = function inPrderTraverse(visit) {        
    if (this.leftChild) inPrderTraverse.call(this.leftChild, visit);
        visit(this.data);
        if (this.rightChild) inPrderTraverse.call(this.rightChild, visit);
    };

　⑴ Wenn p nicht leer ist, wird p auf den Stapel geschoben,

　⑵ Ansonsten (das heißt, p ist leer), lege den Stapel zurück auf p und greife auf das Objekt zu, auf das p zeigt. Knoten, p=p.rightChild; Gehe zu (1); Bis der Stapel leer ist.

　

<br/>

3. Post-Order-Durchquerung des Binärbaums:

1) Rekursiver Algorithmus

Wenn der Binärbaum leer ist, endet die Durchquerung; andernfalls

　⑴ Nachbestellung durch den linken Teilbaum (rufen Sie diesen Algorithmus rekursiv auf);

// 方法1
    inOrder_stack1: function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {                
            stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();
                p.data && visit(p.data);                
                stack.push(p.rightChild);
            }
        }
    },    // 方法2
    inOrder_stack2: function (visit) {        
    var stack = new Stack();        
    var p = this;        
    while (p || stack.top) {            
    if (p) {                
    stack.push(p);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p.data && visit(p.data);
                p = p.rightChild;
            }
        }
    },

　⑵ Nachbestellung durchläuft den rechten Teilbaum (rufen Sie diesen Algorithmus rekursiv auf); Besuchen Sie den Wurzelknoten.

2) Nicht-rekursiver Algorithmus

Beim Post-Order-Traversal ist der Wurzelknoten der zuletzt besuchte. Wenn der Suchzeiger während des Durchlaufvorgangs auf einen bestimmten Wurzelknoten zeigt, kann daher nicht sofort darauf zugegriffen werden, sondern der linke Teilbaum muss zuerst durchlaufen werden und der Wurzelknoten wird auf den Stapel verschoben. Wenn der Wurzelknoten nach dem Durchlaufen seines linken Teilbaums durchsucht wird, ist er immer noch nicht zugänglich und sein rechter Teilbaum muss durchquert werden. Daher muss der Wurzelknoten erneut auf den Stapel verschoben werden, wenn sein rechter Teilbaum durchlaufen und dann wieder auf den Stapel verschoben wird. Richten Sie daher eine Statusflag-Variablenmarke ein:

Mark=0 zeigt an, dass gerade auf diesen Knoten zugegriffen wurde, mark=1 zeigt an, dass die Verarbeitung des linken Teilbaums abgeschlossen ist und zurückgegeben wird,

mark= 2 zeigt an, dass der rechte Teilbaum verarbeitet wird. Ende zurückgeben. Jedes Mal, wenn die Aktion basierend auf dem Markierungsfeld oben im Stapel entschieden wird

Idee zur Algorithmusimplementierung:

// 顺序存储结构的递归后序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('postOrder:');
    void function postOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
        visit(tree[x]);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储的递归后序遍历
    BinaryTree.prototype.postOrderTraverse = function postOrderTraverse(visit) {        
    if (this.leftChild) postOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) postOrderTraverse.call(this.rightChild, visit);
        visit(this.data);
    };

　(1) Der Wurzelknoten wird in den Stapel verschoben und Markierung = 0;

　(2) Wenn der Stapel nicht leer ist, legen Sie ihn auf den Knoten

(3) Wenn die Markierung des Knotens = 0 ist, ändern Sie die Markierung des aktuellen Knotens auf 1, und schiebe den linken Teilbaum auf den Stapel

(4) Wenn die Markierung des Knotens = 1 ist, ändere die Markierung des aktuellen Knotens auf 2 und schiebe den rechten Teilbaum auf den Stapel

　(5) Wenn die Markierung des Knotens = 2 ist, greifen Sie auf den Wert des aktuellen Knotens zu.

　(6) Beenden Sie, bis der Stapel leer ist.

　

Ein konkretes Beispiel

Das obige ist der detaillierte Inhalt vonjs implementiert Datenstrukturen: Baum und Binärbaum, Binärbaumdurchquerung und grundlegende Operationsmethoden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!