Heim >Backend-Entwicklung >PHP-Tutorial >Fortgeschrittenes Kapitel für Programmierer: Das Temperament der Hash-Tabelle
Fortgeschrittenes Kapitel für Programmierer: Das Temperament der Hash-Tabelle
- ringa_leeOriginal
- 2017-09-17 10:16:481485Durchsuche
Herr Zhang Yanpo kam 2016 zu Baishan Cloud Technology und ist hauptsächlich für die Forschung und Entwicklung von Objektspeichern, die Datenverteilung in Computerräumen sowie Reparatur und Problemlösung verantwortlich. Mit dem Ziel, eine Datenspeicherung auf 100PB-Ebene zu erreichen, führte er das Team dazu, den Entwurf, die Implementierung und den Einsatz eines netzwerkweiten verteilten Speichersystems abzuschließen, das „kalte“ und „heiße“ Daten trennte und die Kosten für kalte Daten auf 1,2 senkte mal die Redundanz.
Herr Zhang Yanpo arbeitete von 2006 bis 2015 für Sina und war für das Architekturdesign, die Formulierung des Zusammenarbeitsprozesses, die Codespezifikation und die Implementierung von Standards sowie die Implementierung der meisten Funktionen des Cross-IDC-Cloud-Speicherdienstes auf PB-Ebene verantwortlich. Arbeitete an der Unterstützung von Sinas internen Speicherdiensten wie Weibo, Mikrodisk, Video, SAE, Musik, Software-Downloads usw. Von 2015 bis 2016 war er als leitender technischer Experte bei Meituan tätig und entwarf eine 100 PB-Objektspeicherlösung für alle Computerräume: Entwerfen und implementieren Sie eine Replikationsstrategie für mehrere Kopien mit hoher Parallelität und hoher Zuverlässigkeit und optimieren Sie den Löschcode, um den E/A-Overhead um 90 % zu reduzieren.
In der Softwareentwicklung entspricht eine Hash-Tabelle dem zufälligen Platzieren von n Schlüsseln in b Buckets, um die Speicherung von n Daten in b-Einheitsräumen zu erreichen.
Wir haben einige interessante Phänomene in der Hash-Tabelle gefunden:
Das Verteilungsmuster der Schlüssel in der Hash-Tabelle
Wann die Hash-Tabelle Wenn die Anzahl der Schlüssel und Buckets gleich ist (n/b=1):
37 % der Buckets sind leer
37 % der Buckets enthalten nur 1 Schlüssel
26 % der Buckets haben mehr als 1 Schlüssel (Hash-Konflikt)
Die folgende Abbildung zeigt es intuitiv. Wenn n=b=20, die Anzahl der Schlüssel in jedem Bucket in der Hash-Tabelle (sortieren Sie die Buckets nach der Anzahl der Schlüssel):
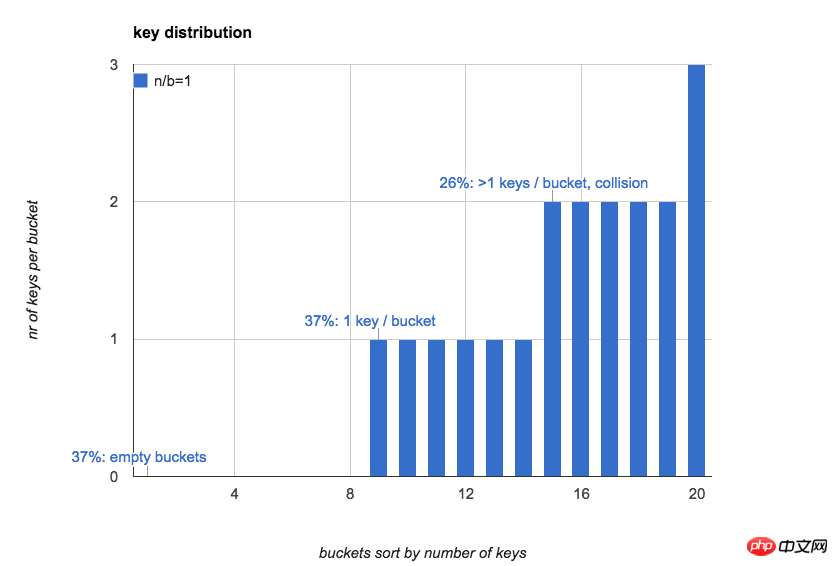
Oft verwenden wir die Hash-Tabelle. Der erste Eindruck ist: Wenn Schlüssel zufällig in alle Buckets gelegt werden, ist die Anzahl der Schlüssel im Bucket relativ einheitlich und die erwartete Anzahl der Schlüssel in jedem Bucket beträgt 1.
Tatsächlich ist die Verteilung der Schlüssel im Bucket sehr ungleichmäßig, wenn n klein ist; wenn n zunimmt, wird sie allmählich durchschnittlich.
Der Einfluss der Anzahl der Schlüssel auf die Anzahl der Buckets in Kategorie 3
Die folgende Tabelle zeigt, wie sich der Wert von n/b auf Kategorie 3 auswirkt, wenn b bestehen bleibt unverändert und n erhöht sich Die folgende Abbildung zeigt die Rate leerer Eimer und den sich ändernden Trend der Konfliktrate mit dem N/B-Wert:
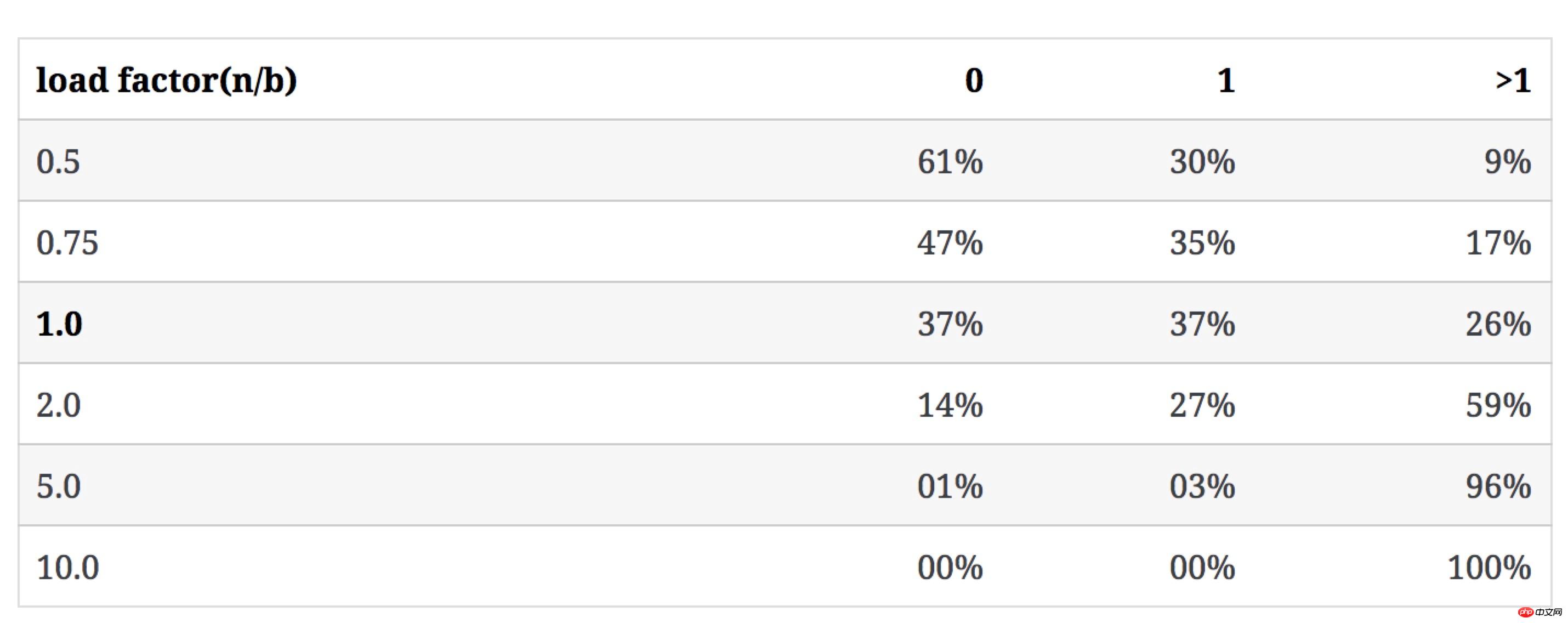
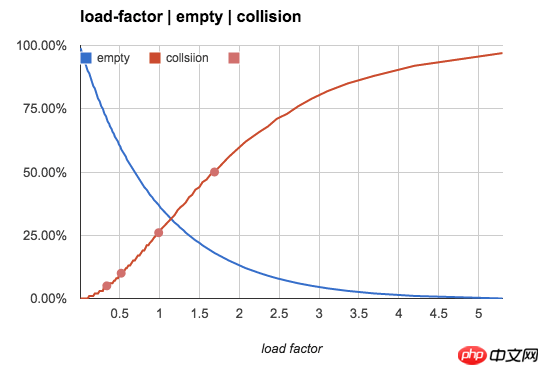
Wenn n/b 1 überschreitet (ein Bucket ermöglicht die Speicherung mehrerer Schlüssel), wird unser Hauptbeobachtungsobjekt zum Verteilungsmuster der Anzahl der Schlüssel im Bucket.
Die folgende Tabelle zeigt den Grad der Ungleichmäßigkeit, wenn n/b groß ist und die Anzahl der Schlüssel in jedem Bucket tendenziell einheitlich ist.Um den Grad der Ungleichmäßigkeit zu beschreiben, verwenden wir das Verhältnis zwischen der maximalen und minimalen Anzahl von Schlüsseln im Eimer ((am wenigsten)/am meisten), um ihn auszudrücken.
In der folgenden Tabelle ist die Verteilung der Schlüssel aufgeführt, wenn n zunimmt, wenn b=100.
Es ist ersichtlich, dass mit zunehmender durchschnittlicher Anzahl von Schlüsseln im Eimer die Ungleichmäßigkeit ihrer Verteilung allmählich abnimmt.
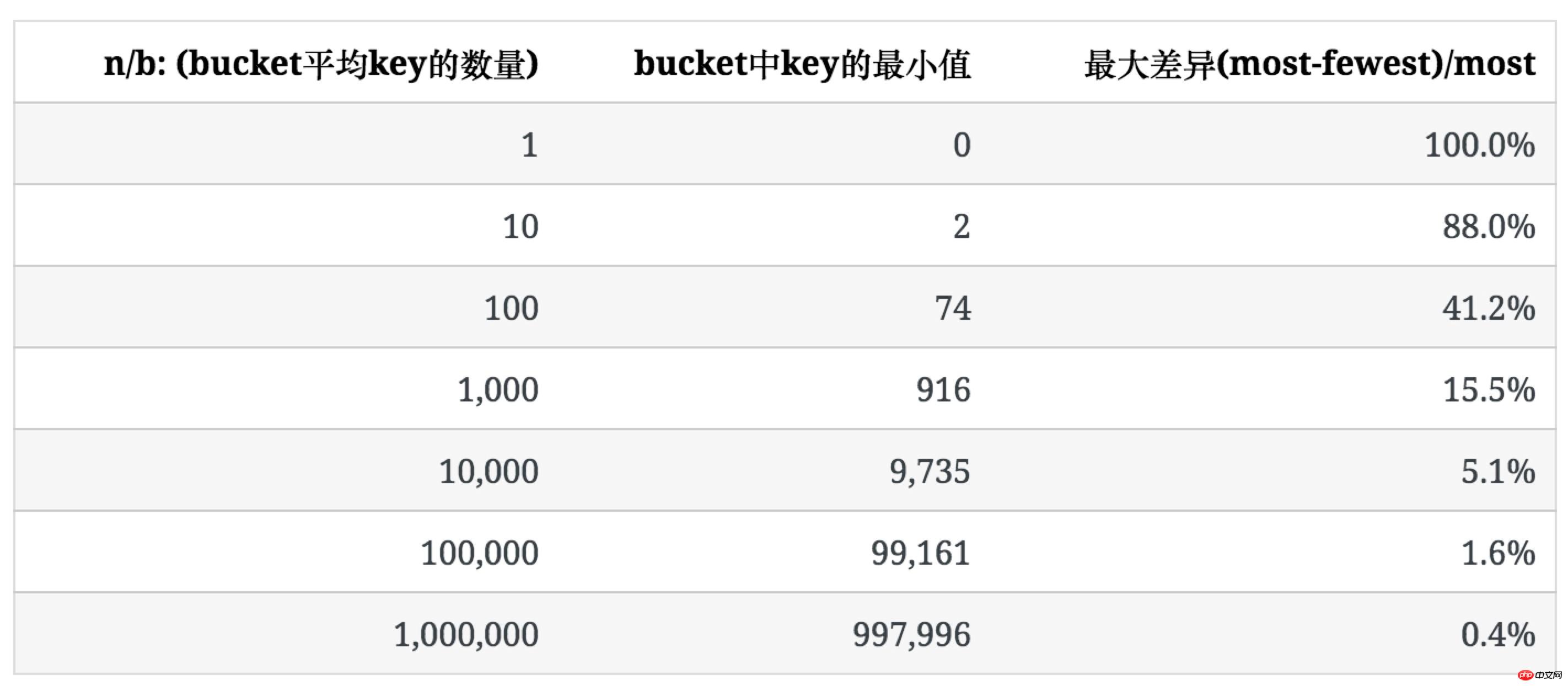
和空bucket或1个key的bucket的占比不同n/b,均匀程度不仅取决于n/b的值,也受b值的影响,后面会提到。 未使用统计中常用的均方差法去描述key分布的不均匀程度,是因为软件开发过程中,更多时候要考虑最坏情况下所需准备的内存等资源。Ein in Hash-Tabellen häufig verwendetes Konzept, der Lastfaktor α=n/b, wird zur Beschreibung verwendet Eigenschaften von Hash-Tabellen.
Normalerweise beträgt sein n/b ≤0,75, basierend auf der Speicher-Hash-Tabelle. Diese Einstellung kann nicht nur Platz sparen, sondern auch die Schlüsselkonfliktrate relativ niedrig halten. Eine niedrige Konfliktrate bedeutet eine langsame Hash-Verschiebung und das Einfügen der Hash-Tabelle erfolgt schneller.
In diesem Szenario von n/b=0,75 sind etwa 47 % der Buckets leer, wenn keine lineare Erkennung verwendet wird (z. B. die Verwendung einer verknüpften Liste im Bucket zum Speichern mehrerer Schlüssel). Bei Verwendung der linearen Erkennung wird von diesen 47 % der Buckets etwa die Hälfte der Buckets durch die lineare Erkennung gefüllt.
线性探测是一个经常被使用的解决插入时hash冲突的算法,它在1个bucket出现冲突时,按照逐步增加的步长顺序向后查看这个bucket后面的bucket,直到找到1个空bucket。因此它对hash的冲突非常敏感。Hash-Tabellen-Funktionstipps:
在很多内存hash表的实现中,选择n/b=<p><strong>Die Hash-Tabelle selbst ist ein Algorithmus, der eine bestimmte Menge Platz gegen Effizienz austauscht. Ein geringer Zeitaufwand (O(1)), eine geringe Speicherplatzverschwendung und eine niedrige Konfliktrate können nicht gleichzeitig erreicht werden. </strong></p>
- Hash-Tabellen eignen sich nur für die Speicherung reiner Speicherdaten Strukturen:
Die Hash-Tabelle tauscht Speicherplatz aus, um die Zugriffsgeschwindigkeit zu erhöhen. Eine kleine Verschwendung von Speicher ist jedoch akzeptabel 🎜 >- Die meisten Hochsprachen (integrierte Hash-Tabelle, Hash-Set usw.) behalten n/b≤Wenn n/b klein ist, verteilt die Hash-Tabelle die Schlüssel nicht gleichmäßig.
- Hash-Tabellen sind nur für Speichermedien mit schnellem Direktzugriff geeignet. Die Datenspeicherung auf der Festplatte erfolgt meist über Btrees oder andere geordnete Datenstrukturen.
Load Factor:n/b>1
另外一种hash表的实现,专门用来存储比较多的key,当 n/b>1n/b1.0时,线性探测失效(没有足够的bucket存储每个key)。这时1个bucket里不仅存储1个key,一般在一个bucket内用chaining,将所有落在这个bucket的key用链表连接起来,来解决冲突时多个key的存储。
链表只在n/b不是很大时适用。因为链表的查找需要O(n)的时间开销,对于非常大的n/b,有时会用tree替代链表来管理bucket内的key。
n/b值较大的使用场景之一是:将一个网站的用户随机分配到多个不同的web-server上,这时每个web-server可以服务多个用户。多数情况下,我们都希望这种分配能尽可能均匀,从而有效利用每个web-server资源。
这就要求我们关注hash的均匀程度。因此,接下来要讨论的是,假定hash函数完全随机的,均匀程度根据n和b如何变化。
n/b 越大,key的分布越均匀
当 n/b 足够大时,空bucket率趋近于0,且每个bucket中key的数量趋于平均。每个bucket中key数量的期望是:
avg=n/b
定义一个bucket平均key的数量是100%:bucket中key的数量刚好是n/b,下图分别模拟了 b=20,n/b分别为 10、100、1000时,bucket中key的数量分布。
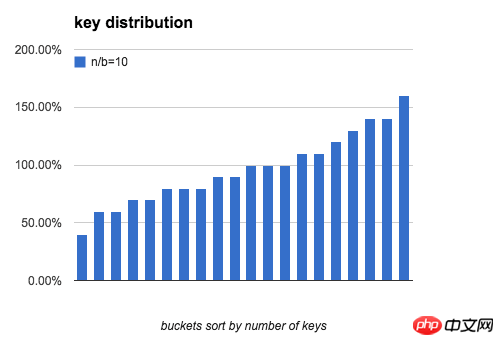
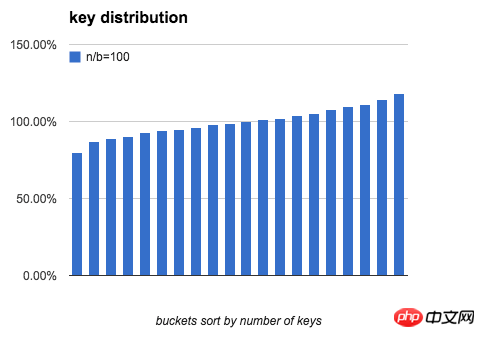
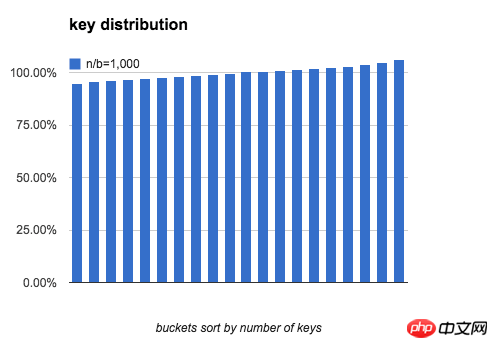
可以看出,当 n/b 增大时,bucket中key数量的最大值与最小值差距在逐渐缩小。下表列出了随b和n/b增大,key分布的均匀程度的变化:
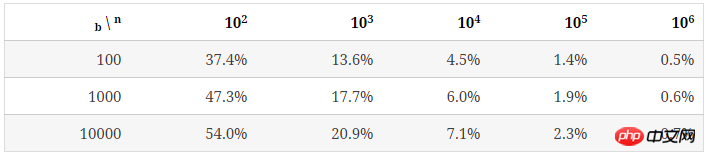
结论:
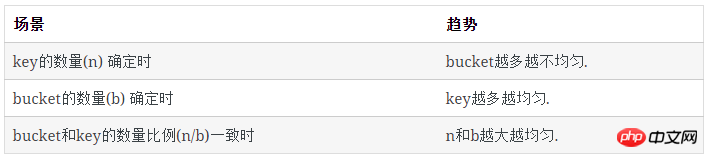
计算
上述大部分结果来自于程序模拟,现在我们来解决从数学上如何计算这些数值。
每类bucket的数量
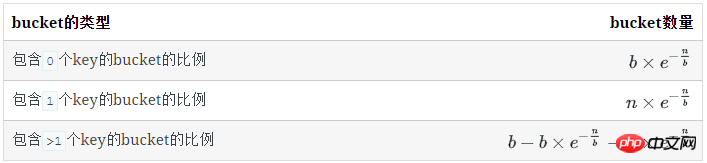
空bucket数量
对于1个key, 它不在某个特定的bucket的概率是 (b−1)/b
所有key都不在某个特定的bucket的概率是( (b−1)/b)n
已知:
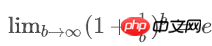
空bucket率是:
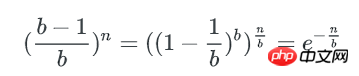
空bucket数量为:

有1个key的bucket数量
n个key中,每个key有1/b的概率落到某个特定的bucket里,其他key以1-(1/b)的概率不落在这个bucket里,因此,对某个特定的bucket,刚好有1个key的概率是:
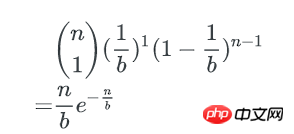
刚好有1个key的bucket数量为:
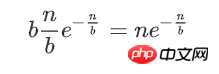
多个key的bucket
剩下即为含多个key的bucket数量:
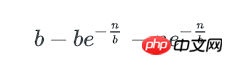
key在bucket中分布的均匀程度
类似的,1个bucket中刚好有i个key的概率是:n个key中任选i个,并都以1/b的概率落在这个bucket里,其他n-i个key都以1-1/b的概率不落在这个bucket里,即:
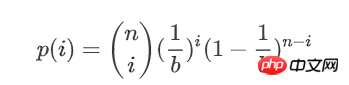
这就是著名的二项式分布。
我们可通过二项式分布估计bucket中key数量的最大值与最小值。
通过正态分布来近似
当 n, b 都很大时,二项式分布可以用正态分布来近似估计key分布的均匀性:
p=1/b,1个bucket中刚好有i个key的概率为:
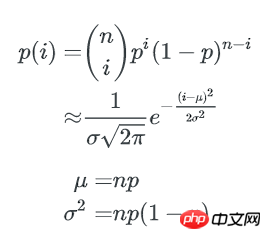
1个bucket中key数量不多于x的概率是:
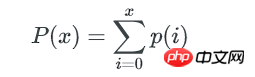
所以,所有不多于x个key的bucket数量是:
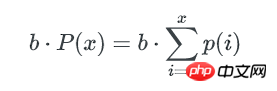
bucket中key数量的最小值,可以这样估算: 如果不多于x个key的bucket数量是1,那么这唯一1个bucket就是最少key的bucket。我们只要找到1个最小的x,让包含不多于x个key的bucket总数为1, 这个x就是bucket中key数量的最小值。
计算key数量的最小值x
一个bucket里包含不多于x个key的概率是:
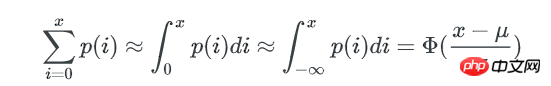
Φ(x) 是正态分布的累计分布函数,当x-μ趋近于0时,可以使用以下方式来近似:
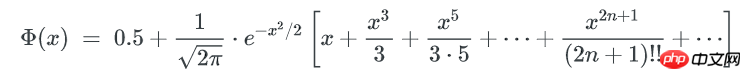
这个函数的计算较难,但只是要找到x,我们可以在[0~μ]的范围内逆向遍历x,以找到一个x 使得包含不多于x个key的bucket期望数量是1。
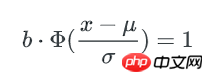
x可以认为这个x就是bucket里key数量的最小值,而这个hash表中,不均匀的程度可以用key数量最大值与最小值的差异来描述: 因为正态分布是对称的,所以key数量的最大值可以用 μ + (μ-x) 来表示。最终,bucket中key数量最大值与最小值的比例就是:
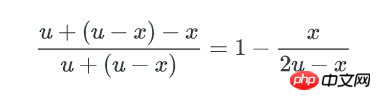
(μ是均值n/b)
程序模拟
以下python脚本模拟了key在bucket中分布的情况,同时可以作为对比,验证上述计算结果。
import sysimport mathimport timeimport hashlibdef normal_pdf(x, mu, sigma):
x = float(x)
mu = float(mu)
m = 1.0 / math.sqrt( 2 * math.pi ) / sigma
n = math.exp(-(x-mu)**2 / (2*sigma*sigma))return m * ndef normal_cdf(x, mu, sigma):
# integral(-oo,x)
x = float(x)
mu = float(mu)
sigma = float(sigma) # to standard form
x = (x - mu) / sigma
s = x
v = x for i in range(1, 100):
v = v * x * x / (2*i+1)
s += v return 0.5 + s/(2*math.pi)**0.5 * math.e ** (-x*x/2)def difference(nbucket, nkey):
nbucket, nkey= int(nbucket), int(nkey) # binomial distribution approximation by normal distribution
# find the bucket with minimal keys.
#
# the probability that a bucket has exactly i keys is:
# # probability density function
# normal_pdf(i, mu, sigma)
#
# the probability that a bucket has 0 ~ i keys is:
# # cumulative distribution function
# normal_cdf(i, mu, sigma)
#
# if the probability that a bucket has 0 ~ i keys is greater than 1/nbucket, we
# say there will be a bucket in hash table has:
# (i_0*p_0 + i_1*p_1 + ...)/(p_0 + p_1 + ..) keys.
p = 1.0 / nbucket
mu = nkey * p
sigma = math.sqrt(nkey * p * (1-p))
target = 1.0 / nbucket
minimal = mu while True:
xx = normal_cdf(minimal, mu, sigma) if abs(xx-target) < target/10: break
minimal -= 1
return minimal, (mu-minimal) * 2 / (mu + (mu - minimal))def difference_simulation(nbucket, nkey):
t = str(time.time())
nbucket, nkey= int(nbucket), int(nkey)
buckets = [0] * nbucket for i in range(nkey):
hsh = hashlib.sha1(t + str(i)).digest()
buckets[hash(hsh) % nbucket] += 1
buckets.sort()
nmin, mmax = buckets[0], buckets[-1] return nmin, float(mmax - nmin) / mmaxif __name__ == "__main__":
nbucket, nkey= sys.argv[1:]
minimal, rate = difference(nbucket, nkey) print 'by normal distribution:'
print ' min_bucket:', minimal print ' difference:', rate
minimal, rate = difference_simulation(nbucket, nkey) print 'by simulation:'
print ' min_bucket:', minimal print ' difference:', rateDas obige ist der detaillierte Inhalt vonFortgeschrittenes Kapitel für Programmierer: Das Temperament der Hash-Tabelle. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- So verwenden Sie cURL zum Implementieren von Get- und Post-Anfragen in PHP
- Alle Ausdruckssymbole in regulären Ausdrücken (Zusammenfassung)

