Detailliertes Beispiel dafür, wie Python die Subset-Tree-Vorlage der Backtracking-Methode verwendet, um das Treppensteigproblem zu lösen

In diesem Artikel wird hauptsächlich die Verwendung der Teilmengenbaumvorlage der Backtracking-Methode durch Python zur Lösung des Treppensteigproblems vorgestellt Need Friends kann sich auf

beziehen. Dieser Artikel beschreibt das Beispiel von Python, das die Teilmengenbaumvorlage der Backtracking-Methode verwendet, um das Treppensteigproblem zu lösen. Teilen Sie es als Referenz mit allen. Die Details lauten wie folgt:

Problem

Eine bestimmte Treppe hat n Stufen, und jede Stufe kann Machen Sie nur 1 Schritt oder 2 Schritte. Wie viele Möglichkeiten gibt es, Treppen von unten nach oben zu steigen?

Analyse

Dieses Problem wurde vor der Anwendung der Divide-and-Conquer-Methode gelöst. Hier werde ich jedoch die Backtracking-Subset-Tree-Vorlage verwenden, um das Problem zu lösen.

Stellen Sie die Methode der Elementzustandsraumanalyse vor: Jeder Schritt ist ein Element, und die Anzahl der möglichen Schritte [1, 2] ist sein Zustandsraum. Es ist nicht schwer zu erkennen, dass die Elemente nicht fixiert sind, aber der Zustandsraum ist fixiert.

Laden Sie den Code direkt hoch.

Code

'''爬楼梯'''
n = 7 # 楼梯阶数
x = []  # 一个解（长度不固定，1-2数组，表示该步走的台阶数）
X = []  # 一组解
# 冲突检测
def conflict(k):
  global n, x, X
  # 部分解步的步数之和超过总台阶数
  if sum(x[:k+1]) > n:
    return True
  return False # 无冲突
# 回溯法（递归版本）
def climb_stairs(k): # 走第k步
  global n, x, X
  if sum(x) == n: # 已走的所有步数之和等于楼梯总台阶数
    print(x)
    #X.append(x[:]) # 保存（一个解）
  else:
    for i in [1, 2]: # 第k步这个元素的状态空间为[1,2]
      x.append(i)
      if not conflict(k): # 剪枝
        climb_stairs(k+1)
      x.pop()       # 回溯
# 测试
climb_stairs(0) # 走第0步

Rendering

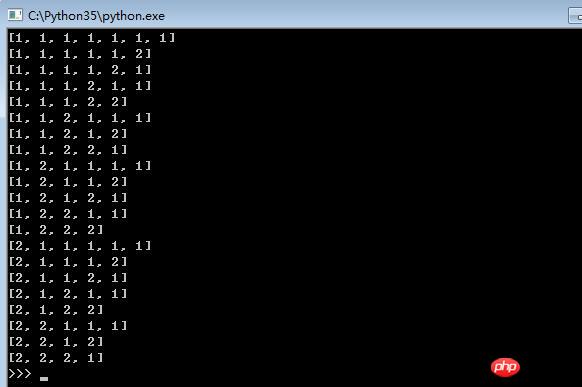
Das obige ist der detaillierte Inhalt vonDetailliertes Beispiel dafür, wie Python die Subset-Tree-Vorlage der Backtracking-Methode verwendet, um das Treppensteigproblem zu lösen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!