Heim >Backend-Entwicklung >Python-Tutorial >Ausführliche Erläuterung der Verwendung von Backtracking-Subset-Tree-Vorlagen durch Python zur Lösung von Labyrinthproblemen
Ausführliche Erläuterung der Verwendung von Backtracking-Subset-Tree-Vorlagen durch Python zur Lösung von Labyrinthproblemen
- 巴扎黑Original
- 2017-09-02 11:43:462137Durchsuche
Dieser Artikel stellt hauptsächlich die Verwendung der Backtracking-Methode zur Lösung von Labyrinthproblemen vor. Er beschreibt kurz die Prinzipien des Labyrinthproblems und analysiert anhand von Beispielen die relevanten Bedienfähigkeiten und Vorsichtsmaßnahmen zur Lösung des Labyrinthproblems in Python basierend auf der Teilmenge der Backtracking-Methode Baumvorlage. Erforderliche Freunde können sich auf
beziehen. Dieser Artikel beschreibt ein Beispiel für die Verwendung der Backtracking-Methode zur Lösung von Labyrinthproblemen in Python. Teilen Sie es allen als Referenz mit. Die Details lauten wie folgt:
Problem
Bei einem Labyrinth ist der Eingang bekannt. Fragen Sie, ob es einen Weg vom Eingang zum Ausgang gibt, und wenn ja, geben Sie einen solchen Weg aus. Beachten Sie, dass die Bewegung in acht Richtungen ausgeführt werden kann: oben, unten, links, rechts, oben links, oben rechts, unten links und unten rechts. Die Eingabe von 0 im Labyrinth bedeutet, dass es begehbar ist, und die Eingabe von 1 bedeutet, dass es sich um eine Wand handelt. Umgeben Sie das Labyrinth der Einfachheit halber mit 1, um Grenzprobleme zu vermeiden.
Analyse
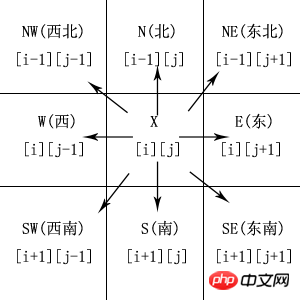
Angesichts der Tatsache, dass links und rechts relativ sind, wird es in acht Richtungen modifiziert: Norden, Nordosten, Osten, Südosten, Süden, Südwesten, Westen und Nordwesten. In jedem Raster stehen 8 Richtungen zur Auswahl, also 8 Zustände zur Auswahl. Daher müssen diese 8 Zustände ausgehend vom Eingangsgitter jedes Mal durchlaufen werden, wenn ein Gitter betreten wird.
Natürlich kann die Teilmengenbaumvorlage der Backtracking-Methode angewendet werden.
Beachten Sie, dass die Länge der Lösung nicht festgelegt ist.
Code
# 迷宫(1是墙,0是通路)
maze = [[1,1,1,1,1,1,1,1,1,1],
[0,0,1,0,1,1,1,1,0,1],
[1,1,0,1,0,1,1,0,1,1],
[1,0,1,1,1,0,0,1,1,1],
[1,1,1,0,0,1,1,0,1,1],
[1,1,0,1,1,1,1,1,0,1],
[1,0,1,0,0,1,1,1,1,0],
[1,1,1,1,1,0,1,1,1,1]]
m, n = 8, 10 # 8行,10列
entry = (1,0) # 迷宫入口
path = [entry] # 一个解(路径)
paths = [] # 一组解
# 移动的方向(顺时针8个:N, EN, E, ES, S, WS, W, WN)
directions = [(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1)]
# 冲突检测
def conflict(nx, ny):
global m,n,maze
# 是否在迷宫中,以及是否可通行
if 0 <= nx < m and 0 <= ny < n and maze[nx][ny]==0:
return False
return True
# 套用子集树模板
def walk(x, y): # 到达(x,y)格子
global entry,m,n,maze,path,paths,directions
if (x,y) != entry and (x % (m-1) ==0 or y % (n-1) == 0): # 出口
#print(path)
paths.append(path[:]) # 直接保存,未做最优化
else:
for d in directions: # 遍历8个方向(亦即8个状态)
nx, ny = x+d[0], y+d[1]
path.append((nx,ny)) # 保存,新坐标入栈
if not conflict(nx, ny): # 剪枝
maze[nx][ny] = 2 # 标记,已访问(奇怪,此两句只能放在if区块内!)
walk(nx, ny)
maze[nx][ny] = 0 # 回溯,恢复
path.pop() # 回溯,出栈
# 解的可视化(根据一个解x,复原迷宫路径,'2'表示通路)
def show(path):
global maze
import pprint, copy
maze2 = copy.deepcopy(maze)
for p in path:
maze2[p[0]][p[1]] = 2 # 通路
pprint.pprint(maze) # 原迷宫
print()
pprint.pprint(maze2) # 带通路的迷宫
# 测试
walk(1,0)
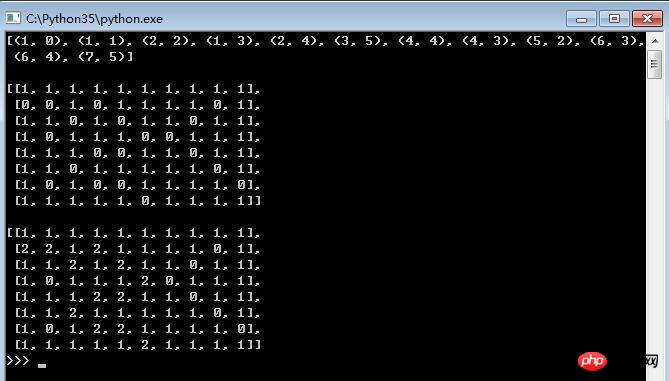
print(paths[-1], '\n') # 看看最后一条路径
show(paths[-1])Rendering
Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung der Verwendung von Backtracking-Subset-Tree-Vorlagen durch Python zur Lösung von Labyrinthproblemen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

