Heim >Java >javaLernprogramm >Empfohlene Ressourcen für Mahout-Video-Tutorials
Empfohlene Ressourcen für Mahout-Video-Tutorials
- 黄舟Original
- 2017-09-01 10:01:391602Durchsuche
Mahout bietet einige skalierbare Implementierungen klassischer Algorithmen im Bereich des maschinellen Lernens mit dem Ziel, Entwicklern dabei zu helfen, intelligente Anwendungen bequemer und schneller zu erstellen. Mahout enthält viele Implementierungen, einschließlich Clustering, Klassifizierung, Empfehlungsfilterung und häufiges Unterelement-Mining. Darüber hinaus kann Mahout mithilfe der Apache Hadoop-Bibliothek effizient in die Cloud skalieren.

Der Unterrichtsstil des Lehrers:
Die Vorträge des Lehrers sind einfach, klar, schichtweise analysiert, ineinandergreifend und Strenge Argumentation, hat eine strenge Struktur, nutzt die logische Kraft des Denkens, um die Aufmerksamkeit der Schüler zu erregen, und nutzt Vernunft, um den Unterrichtsprozess im Klassenzimmer zu steuern. Durch das Anhören der Vorlesungen des Lehrers lernen die Schüler nicht nur Wissen, sondern erhalten auch eine Denkschulung und werden auch von der strengen akademischen Haltung des Lehrers beeinflusst und beeinflusst
Der schwierigere Punkt in diesem Video ist die Logistik regression classifier_Bei Yessian Classifier_1:
1. Hintergrund
Lassen Sie uns zunächst einige Fragen stellen Fragen: Wenn Sie diese Fragen beantworten können, müssen Sie diesen Artikel nicht lesen, da Ihre Motivation zum Lesen lediglich darin besteht, Fehler in diesem Artikel zu finden. Bitte senden Sie eine E-Mail an „Naive Bayesian“. of Faults“ an 297314262 @qq.com, ich werde Ihren Brief sorgfältig lesen.
Übrigens, wenn Sie nach dem Lesen dieses Artikels die folgenden Fragen immer noch nicht beantworten können, benachrichtigen Sie mich bitte per E-Mail und ich werde mein Bestes tun, um Ihre Zweifel zu beantworten.
Das „naive“ im Naive-Bayes-Klassifikator bezieht sich speziell auf die Eigenschaften dieses Klassifikators
Naive-Bayes-Klassifikator und Maximum-Likelihood-Schätzung (MLE), Maximum-Posteriori-Wahrscheinlichkeitsbeziehung (MAP)
Naive Bayes-Klassifizierung, logistische Regressionsklassifizierung, generatives Modell und Entscheidungsmodell
Die Beziehung zwischen überwachtem Lernen und Bayes'scher Schätzung
2 Übereinstimmung
Das ist also so Artikel beginnt. Was die verschiedenen Ausdrucksformen betrifft, die in diesem Artikel vorkommen können, werden hier zunächst einige Konventionen getroffen.
Großbuchstaben wie X stellen Zufallsvariablen dar; wenn X eine mehrdimensionale Variable ist, dann der Index i stellt die i-te Dimensionsvariable dar. Das heißt, Xi
Kleinbuchstaben wie Xij repräsentieren einen Wert der Variablen (den j-ten Wert von Xi)
3 Überwachtes Lernen
Okay, also beantworten Sie zuerst die vierte Frage: Wie kann die Bayes'sche Schätzung verwendet werden, um Probleme beim überwachten Lernen zu lösen?
Für überwachtes Lernen besteht unser Ziel tatsächlich darin, eine Zielfunktion f zu schätzen: Die Variable Y ist das tatsächliche Klassifizierungsergebnis der Stichprobe. Angenommen, der Wert der Stichprobe |X=xk), finden Sie einfach alle Schätzungen von P(X=xk|Y=yi) und alle Schätzungen von P(Y=yi) basierend auf der Stichprobe. Der anschließende Klassifizierungsprozess besteht darin, das größte yi von P(Y=yi|X=xk) zu finden. Es ist ersichtlich, dass die Verwendung der Bayes'schen Schätzung das Problem des überwachten Lernens lösen kann.
4. „Naive“ Eigenschaften von Klassifikatoren 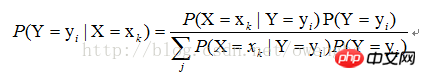
Wie oben erwähnt, kann die Lösung von P(X=xk|Y=yi) in die Lösung von P(X1=x1j1|Y=yi), P(X2=x2j2|Y=yi) umgewandelt werden. .. P (Xn=xnjn|Y=yi), wie verwendet man dann die Maximum-Likelihood-Schätzmethode, um diese Werte zu finden?
Zuerst müssen wir verstehen, was Maximum-Likelihood-Schätzung ist. Tatsächlich geht es in unseren Lehrbüchern zur Wahrscheinlichkeitstheorie ausschließlich um die Lösung unbeaufsichtigter Lernprobleme. Sie sollten verstehen, dass die Verwendung der Maximum-Likelihood-Schätzung zur Lösung überwachter Lernprobleme unter naiven Merkmalen tatsächlich die Verwendung der Maximum-Likelihood-Schätzung zur Lösung unbeaufsichtigter Lernprobleme unter verschiedenen Kategorien von Bedingungen bedeutet.
Das obige ist der detaillierte Inhalt vonEmpfohlene Ressourcen für Mahout-Video-Tutorials. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

