Grundlegende und häufig verwendete Algorithmen in Python

Dieser Artikel konzentriert sich hauptsächlich auf das Erlernen häufig verwendeter Algorithmen in Python. Interessierte Freunde können sich auf den Inhalt dieses Abschnitts beziehen >

Algorithmusdefinition

ZeitkomplexitätRaumkomplexitätGemeinsame Algorithmusbeispiele

1. Algorithmusdefinition

Algorithmus bezieht sich auf eine genaue und vollständige Beschreibung einer Problemlösung. Es handelt sich um eine Reihe klarer Anweisungen zur Lösung von Problemen, die eine systematische Methode zur Beschreibung des strategischen Mechanismus zur Lösung von Problemen darstellen. Mit anderen Worten: Es ist möglich, für bestimmte standardisierte Inputs innerhalb einer begrenzten Zeit den erforderlichen Output zu erhalten. Wenn ein Algorithmus fehlerhaft oder für ein Problem ungeeignet ist, wird die Ausführung des Algorithmus das Problem nicht lösen. Verschiedene Algorithmen können unterschiedliche Zeit, Raum oder Effizienz nutzen, um dieselbe Aufgabe zu erledigen. Die Qualität eines Algorithmus kann an seiner räumlichen und zeitlichen Komplexität gemessen werden. Ein Algorithmus sollte die folgenden sieben wichtigen Eigenschaften aufweisen:

①Endlichkeit: Die Endlichkeit eines Algorithmus bedeutet, dass der Algorithmus nach der Ausführung einer begrenzten Anzahl von Schritten terminieren kann; 🎜>②Bestimmtheit: Jeder Schritt des Algorithmus muss eine genaue Definition haben.

③Eingabe: Ein Algorithmus hat 0 oder mehr Eingaben zur Beschreibung des Operanden. Die Ausgangssituation, die sogenannte 0-Eingabe, bezieht sich auf die festgelegten Anfangsbedingungen durch den Algorithmus selbst;

④Ausgabe: Ein Algorithmus verfügt über eine oder mehrere Ausgaben, um die Ergebnisse der Verarbeitung der Eingabedaten widerzuspiegeln. Ein Algorithmus ohne Ausgabe ist bedeutungslos.

⑤Effektivität: Jeder im Algorithmus ausgeführte Berechnungsschritt kann in grundlegende ausführbare Operationsschritte zerlegt werden, d. h. jeder Berechnungsschritt kann innerhalb einer begrenzten Zeit abgeschlossen werden (auch als Wirksamkeit bezeichnet). ;

⑥Hohe Effizienz: schnelle Ausführung und geringer Ressourcenverbrauch;

⑦Robustheit (Robustheit): Korrekte Reaktion auf Daten.

2. Zeitkomplexität

In der Informatik ist die Zeitkomplexität eines Algorithmus eine Funktion, die die Funktionsweise des Algorithmus quantitativ beschreibt. Die häufig verwendete Big-O-Notation ist eine mathematische Notation, die zur Beschreibung des asymptotischen Verhaltens einer Funktion verwendet wird. Genauer gesagt handelt es sich um eine Funktion, die anhand einer anderen (normalerweise einfacheren) Funktion beschrieben wird In der Mathematik wird es im Allgemeinen verwendet, um die verbleibenden Terme von abgeschnittenen unendlichen Reihen zu charakterisieren. In der Informatik ist es sehr nützlich, die Komplexität von Algorithmen zu analysieren Komplexität kann als asymptotisch bezeichnet werden, was die Situation berücksichtigt, in der sich die Größe des Eingabewerts der Unendlichkeit nähert.

Großes O, kurz gesagt kann man es sich als „Ordnung von“ (ungefähr) vorstellen.

Unendlich asymptotisch

Die Big-O-Notation ist sehr nützlich bei der Analyse der Effizienz eines Algorithmus. Beispielsweise kann die Zeit, die zum Lösen eines Problems der Größe n benötigt wird (oder die Anzahl der erforderlichen Schritte), ermittelt werden: T(n) = 4n^2 - 2n + 2.

Wenn n zunimmt, wird der Term n^2; In den meisten Fällen ist die Auswirkung des Weglassens auf den Wert des Ausdrucks vernachlässigbar.

Mathematische Darstellungskompetenz Tutorial zum Darstellungskonzept von Python

1. Berechnungsmethode

1 Algorithmus kann nicht theoretisch berechnet werden und kann nur durch Ausführen eines Tests auf dem Computer ermittelt werden. Aber es ist für uns unmöglich und unnötig, jeden Algorithmus auf dem Computer zu testen. Wir müssen nur wissen, welcher Algorithmus mehr Zeit benötigt und welcher weniger Zeit benötigt. Und die Zeit, die ein Algorithmus benötigt, ist proportional zur Anzahl der Ausführungen von Anweisungen im Algorithmus. Je mehr Anweisungen der Algorithmus hat, desto mehr Zeit benötigt er.

Die Anzahl der Anweisungsausführungen in einem Algorithmus wird als Anweisungshäufigkeit oder Zeithäufigkeit bezeichnet. Bezeichnen Sie es als T(n).

2. Im Allgemeinen ist die Häufigkeit, mit der die Grundoperation des Algorithmus wiederholt wird, eine Funktion f(n) des Moduls n. Daher wird die zeitliche Komplexität des Algorithmus aufgezeichnet : T ( n)=O(f(n)). Mit zunehmendem Modul n ist die Wachstumsrate der Algorithmusausführungszeit proportional zur Wachstumsrate von f(n). Je kleiner f(n), desto geringer ist die Zeitkomplexität des Algorithmus und desto höher ist die Effizienz des Algorithmus .

Ermitteln Sie bei der Berechnung der Zeitkomplexität zunächst die Grundoperationen des Algorithmus, bestimmen Sie dann seine Ausführungszeiten basierend auf den entsprechenden Anweisungen und ermitteln Sie dann die gleiche Größenordnung von T(n) (seine gleiche Größenordnung sind). wie folgt: 1 , Log2n, n, nLog2n, n Quadrat, n Würfel, 2 n Potenz, n!), nachdem ich herausgefunden habe, dass f (n) = diese Größenordnung ist, wenn T (n)/f (n) gefunden wird Die Grenze Eine Konstante c kann erhalten werden, und die Zeitkomplexität T(n)=O(f(n)).

3. Häufige Zeitkomplexitäten

sind in aufsteigender Reihenfolge angeordnet:
Konstante Ordnung O(1), Logarithmische Ordnung O( log2n), lineare Ordnung O(n), lineare logarithmische Ordnung O(nlog2n), quadratische Ordnung O(n^2), kubische Ordnung O(n^3),..., k-te Potenzordnung O(n ^k), Exponentielle Ordnung O(2^n).
Unter ihnen

1.O(n), O(n^2), kubische Ordnung O(n^3),..., k-te Ordnung O(n^k) sind Zeitkomplexität polynomialer Ordnung bzw. Zeit erster Ordnung genannt Komplexität, Zeitkomplexität zweiter Ordnung. . . .
2.O(2^n), exponentielle Zeitkomplexität, diese Art ist unpraktisch
3 Logarithmische Ordnung O(log2n), lineare logarithmische Ordnung O(nlog2n), mit Ausnahme der konstanten Ordnung, dies ist die effizienteste

Beispiel: Algorithmus:

 for（i=1;i<=n;++i）
 {
 for(j=1;j<=n;++j)
 {
 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
 for(k=1;k<=n;++k)
 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
 }
 }

Dann gibt es T(n) = n^2+n^ 3. Gemäß Auf die gleiche Größenordnung in den Klammern oben können wir bestimmen, dass n^3 die gleiche Größenordnung wie T(n) hat
Dann haben wir f(n) = n^3 und finden es dann entsprechend T(n)/f(n) Der Grenzwert kann durch die Konstante c erhalten werden
Dann ist die zeitliche Komplexität des Algorithmus: T(n)=O(n^3)

4. Definition: Wenn ein Problem die Skala n hat und die Zeit, die ein bestimmter Algorithmus zur Lösung dieses Problems benötigt, T(n) ist, wird eine bestimmte Funktion von T(n) als „ bezeichnet. „Zeitkomplexität“ dieses Algorithmus.

Wenn die Eingabemenge n allmählich zunimmt, wird der Grenzfall der Zeitkomplexität als „asymptotische Zeitkomplexität“ des Algorithmus bezeichnet.

Wir verwenden oft die große O-Notation, um die Zeitkomplexität auszudrücken. Beachten Sie, dass es sich um die Zeitkomplexität eines bestimmten Algorithmus handelt. Big O bedeutet, dass es per Definition eine Obergrenze gibt, wenn f(n)=O(n), dann gilt f(n)=O(n^2). ein Supremum, aber die Menschen sind es im Allgemeinen gewohnt, beim Ausdrücken das erstere auszudrücken.

Darüber hinaus hat ein Problem selbst auch seine Komplexität. Wenn die Komplexität eines Algorithmus die untere Grenze der Komplexität des Problems erreicht, wird ein solcher Algorithmus als bester Algorithmus bezeichnet.

„Big O-Notation“: Der in dieser Beschreibung verwendete Grundparameter ist n, die Größe der Probleminstanz, die die Komplexität oder Laufzeit als Funktion von n ausdrückt. Das „O“ stellt hier die Reihenfolge dar. „Binäre Suche ist O(logn)“, was bedeutet, dass „ein Array der Größe n über logn-Schritte abgerufen werden muss“. dass, wenn n zunimmt, die Laufzeit höchstens proportional zu f(n) zunimmt.

Diese asymptotische Schätzung ist für die theoretische Analyse und den groben Vergleich von Algorithmen sehr wertvoll, aber Details können in der Praxis auch zu Unterschieden führen. Beispielsweise kann ein O(n2)-Algorithmus mit geringem Overhead für kleine n schneller laufen als ein O(nlogn)-Algorithmus mit hohem Overhead. Wenn n groß genug wird, müssen Algorithmen mit langsamer ansteigenden Funktionen natürlich schneller arbeiten.

O(1)

Temp=i;i=j;j=temp; Die Häufigkeit von ist alle 1 und die Ausführungszeit davon Das Programmsegment ist eine von der Problemgröße n unabhängige Konstante. Die zeitliche Komplexität des Algorithmus ist konstanter Ordnung und wird als T(n)=O(1) aufgezeichnet. Wenn die Ausführungszeit des Algorithmus mit zunehmender Problemgröße n nicht zunimmt, ist seine Ausführungszeit nur eine große Konstante, selbst wenn der Algorithmus Tausende von Anweisungen enthält. Die zeitliche Komplexität dieses Algorithmustyps beträgt O(1).

O(n^2)

2.1 Tauschen Sie den Inhalt von i und j aus

sum=0; (einmal) for(i=1;i9e97613297d5c55a07d3950d7771e35elinker Teilbaum->rechter Teilbaum

Durchquerung in der Reihenfolge: linker Teilbaum->Wurzelknoten->rechter Teilbaum

Post-Order-Durchquerung: linker Teilbaum->rechter Teilbaum->Wurzelknoten

Zum Beispiel: Finden Sie drei Durchquerungen des folgenden Baums

Durchquerung vor der Bestellung: abdefgc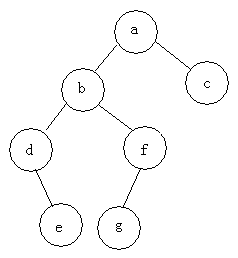

Durchquerung in der Reihenfolge: debgfac

Durchquerung nach der Bestellung: edgfbca

Typ des Binärbaums

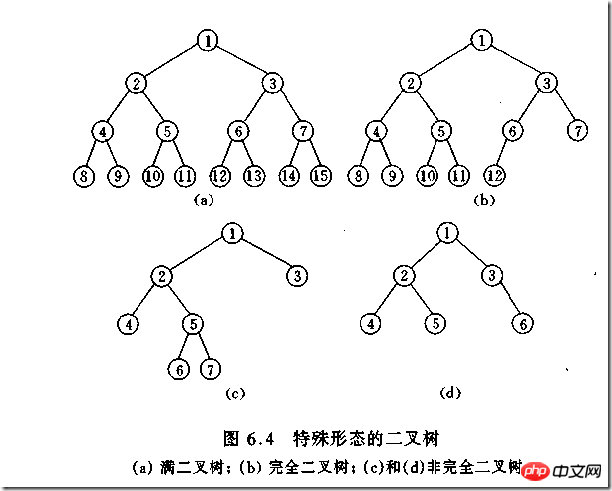
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

如何判断平衡二叉树？

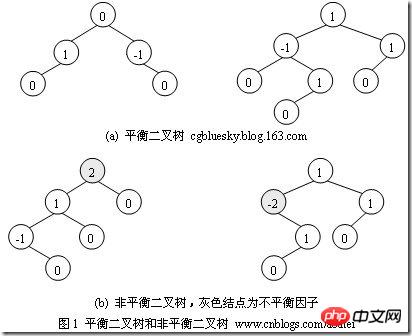
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树遍历实现

class TreeNode(object):
 def __init__(self,data=0,left=0,right=0):
 self.data = data
 self.left = left
 self.right = right
 
class BTree(object):
 def __init__(self,root=0):
 self.root = root
 
 
 def preOrder(self,treenode):
 if treenode is 0:
 return
 print(treenode.data)
 self.preOrder(treenode.left)
 self.preOrder(treenode.right)
 def inOrder(self,treenode):
 if treenode is 0:
 return
 self.inOrder(treenode.left)
 print(treenode.data)
 self.inOrder(treenode.right)
 
 def postOrder(self,treenode):
 if treenode is 0:
 return
 self.postOrder(treenode.left)
 self.postOrder(treenode.right)
 print(treenode.data)
if __name__ == '__main__':
 n1 = TreeNode(data=1)
 n2 = TreeNode(2,n1,0)
 n3 = TreeNode(3)
 n4 = TreeNode(4)
 n5 = TreeNode(5,n3,n4)
 n6 = TreeNode(6,n2,n5)
 n7 = TreeNode(7,n6,0)
 n8 = TreeNode(8)
 root = TreeNode('root',n7,n8)
 
 bt = BTree(root)
 print("preOrder".center(50,'-'))
 print(bt.preOrder(bt.root))
 
 print("inOrder".center(50,'-'))
 print (bt.inOrder(bt.root))
 
 print("postOrder".center(50,'-'))
 print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
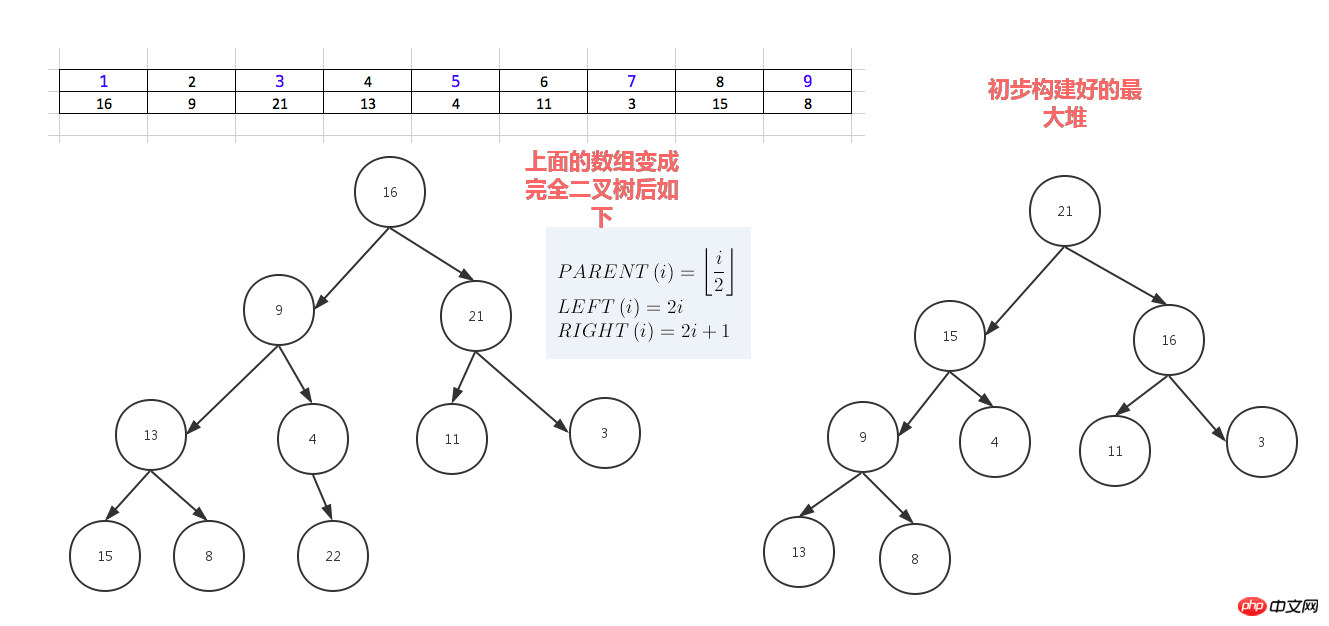
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
 root = node
 #print(root,2*root+1,end)
 while True:
 # 从root开始对最大堆调整
 
 child = 2 * root +1 #left child
 if child > end:
 #print('break',)
 break
 print("v:",root,arr[root],child,arr[child])
 print(arr)
 # 找出两个child中交大的一个
 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
 child += 1 #设置右边为大
 
 if arr[root] < arr[child]:
 # 最大堆小于较大的child, 交换顺序
 tmp = arr[root]
 arr[root] = arr[child]
 arr[child]= tmp
 
 # 正在调整的节点设置为root
 #print("less1:", arr[root],arr[child],root,child)
 
 root = child #
 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
 #print("less2:", arr[root],arr[child],root,child)
 else:
 # 无需调整的时候, 退出
 break
 #print(arr)
 print(&#39;-------------&#39;)
 
def heap_sort(arr):
 # 从最后一个有子节点的孩子还是调整最大堆
 first = len(arr) // 2 -1
 for i in range(first, -1, -1):
 sift_down(arr, i, len(arr) - 1)
 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
 print(&#39;--------end---&#39;,arr)
 # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
 for end in range(len(arr) -1, 0, -1):
 arr[0], arr[end] = arr[end], arr[0]
 sift_down(arr, 0, end - 1)
 #print(arr)
def main():
 # [7, 95, 73, 65, 60, 77, 28, 62, 43]
 # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
 array = [16,9,21,13,4,11,3,22,8,7,15,29]
 #array = []
 #for i in range(2,5000):
 # #print(i)
 # array.append(random.randrange(1,i))
 
 print(array)
 start_t = time.time()
 heap_sort(array)
 end_t = time.time()
 print("cost:",end_t -start_t)
 print(array)
 #print(l)
 #heap_sort(l)
 #print(l)
 
 
if __name__ == "__main__":
 main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
 print("-------",dataset[0:i+1],len(dataset),i)
 #for index in range(int(len(dataset)/2),0,-1):
 for index in range(int((i+1)/2),0,-1):
 print(index)
 p_index = index

 l_child_index = p_index *2 - 1
 r_child_index = p_index *2
 print("l index",l_child_index,'r index',r_child_index)
 p_node = dataset[p_index-1]
 left_child = dataset[l_child_index]

 if p_node < left_child: # switch p_node with left child
 dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
 #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
 #print(left_child)
 right_child = dataset[r_child_index]
 print(p_index,p_node,left_child,right_child)

 # if p_node < left_child: #switch p_node with left child
 # dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
 # # redefine p_node after the switch ,need call this val below
 # p_node = dataset[p_index - 1]
 #
 if p_node < right_child: #swith p_node with right child
 dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 else:
 print("p node [%s] has no right child" % p_node)


 #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

 print("switch i index", i, dataset[0], dataset[i] )
 print("before switch",dataset[0:i+1])
 dataset[0],dataset[i] = dataset[i],dataset[0]
 print(dataset)

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

首先要明确一下增量的取法：

第一次增量的取法为： d=count/2;

第二次增量的取法为: d=(count/2)/2;

最后一直到: d=1;

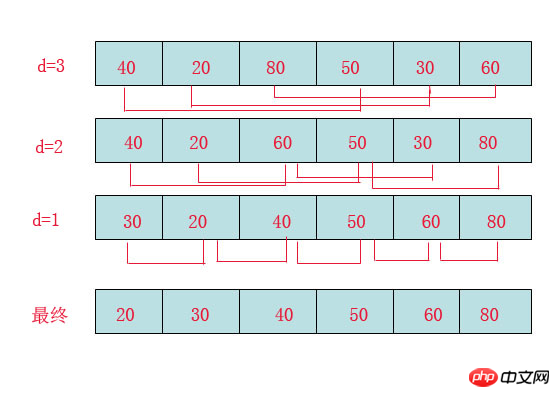
看上图观测的现象为：

d=3时：将40跟50比，因50大，不交换。

              将20跟30比，因30大，不交换。

              将80跟60比，因60小，交换。

d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

              将20跟50比，不交换，继续将50跟80比，不交换。

d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

希尔排序代码

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
 print("---step ---", step)
 #对分组数据进行插入排序

 for index in range(0,len(source)):
 if index + step < len(source):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 if current_val > source[index+step]: #switch
 source[index], source[index+step] = source[index+step], source[index]

 step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
 for index in range(1, len(source)):
 current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
 position = index

 while position > 0 and source[
  position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position - 1] # 把左边的一个元素往右移一位
 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

t_end = time.time() - t_start

print("cost:",t_end)

Das obige ist der detaillierte Inhalt vonGrundlegende und häufig verwendete Algorithmen in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!