Heim >Java >javaLernprogramm >Detaillierte Erläuterung der Binär- und Bitoperationen in Java
Detaillierte Erläuterung der Binär- und Bitoperationen in Java
- 零下一度Original
- 2017-07-16 16:58:514132Durchsuche
1. Darstellungsmethode:
In der Java-Sprache werden Binärzahlen durch Zweierkomplement dargestellt, das höchste Bit ist das Vorzeichenbit, das Vorzeichenbit positiver Zahlen ist 0, und das Vorzeichenbit negativer Zahlen ist 1. Die Darstellung des Komplementcodes muss die folgenden Anforderungen erfüllen.
(1) Das höchste Bit einer positiven Zahl ist 0, und die verbleibenden Bits stellen den Wert selbst dar (Binärzahl).
(2) Bei einer negativen Zahl wird das Komplement des Absolutwerts der Zahl bitweise invertiert und dann 1 zur gesamten Zahl addiert.
Bitweise OperationenAusdruck besteht aus Operanden und bitweisen Operatoren, die den GanzzahltypBitweise ausführen Operationen mit Binärzahlen. Bitoperatoren können in logische Operatoren (einschließlich ~, &, | und ^) und Schiebeoperatoren (einschließlich >>, << und >>>) unterteilt werden.
1) Der linke Verschiebungsoperator (<<) kann den Operanden auf der linken Seite des Operators um die auf der rechten Seite des Operators angegebene Anzahl von Ziffern nach links verschieben (durch Auffüllen von 0). Low-Bit).
2) Der „vorzeichenbehaftete“ Rechtsverschiebungsoperator (>>) verschiebt den Operanden auf der linken Seite des Operators um die auf der rechten Seite des Operators angegebene Anzahl von Ziffern nach rechts. Der „vorzeichenbehaftete“ Rechtsverschiebungsoperator verwendet eine „Vorzeichenerweiterung“: Wenn der Wert positiv ist, wird 0 in das High-Bit eingefügt; wenn der Wert negativ ist, wird 1 in das High-Bit eingefügt.
3) Java hat außerdem einen „vorzeichenlosen“ Rechtsverschiebungsoperator (>>>) hinzugefügt, der eine „Nullerweiterung“ verwendet: Unabhängig davon, ob positiv oder negativ, werden an der Spitze Nullen eingefügt Bits. Dieser Operator ist in C oder C++ nicht verfügbar.
4) Wenn char, byte oder short verschoben werden, werden sie automatisch in ein int konvertiert, bevor die Verschiebung durchgeführt wird. Es werden nur die 5 Low-Bits rechts verwendet. Dies verhindert, dass wir eine unrealistische Anzahl von Ziffern innerhalb eines int verschieben. Wenn ein langer Wert verarbeitet wird, ist das erhaltene Endergebnis ebenfalls lang. Zu diesem Zeitpunkt werden nur die 6 niedrigen Bits auf der rechten Seite verwendet, um zu verhindern, dass die Bewegung die Anzahl der vorgefertigten Ziffern im langen Wert überschreitet. Es kann aber auch zu Problemen kommen, wenn Sie „vorzeichenlose“ Rechtsverschiebungen durchführen. Wenn Sie eine Rechtsverschiebungsoperation für ein Byte oder einen kurzen Wert durchführen, ist das Ergebnis möglicherweise nicht korrekt (insbesondere Java 1.0 und Java 1.1). Sie werden automatisch in den Typ int konvertiert und nach rechts verschoben. Eine „Null-Erweiterung“ kommt jedoch nicht vor, sodass Sie in diesen Fällen ein Ergebnis von -1 erhalten.
Binär ist ein in der Computertechnologie weit verbreitetes Zahlensystem. Binärdaten sind eine Zahl, die durch zwei Ziffern, 0 und 1, dargestellt wird. Seine Basis ist 2, die Übertragsregel ist „zwei zu eins“ und die Entlehnungsregel ist „eins zu gleich zwei entleihen“. Sie wurde von Leibniz, dem deutschen Meister der mathematischen Philosophie, im 18. Jahrhundert entdeckt. Das aktuelle Computersystem verwendet grundsätzlich ein Binärsystem, und Daten werden hauptsächlich in Form von Zweierkomplementcodes in Computern gespeichert. Das Binärsystem im Computer ist ein sehr kleiner Schalter, wobei „Ein“ für 1 und „Aus“ für 0 steht.
Wie sieht Binärdatei in Java aus? Lassen Sie uns gemeinsam seinen geheimnisvollen Schleier lüften.
1. Javas integrierte Dezimalkonvertierung
Die grundlegenden Berechnungsmethoden für die Konvertierung von Dezimalzahlen in Binärzahlen und die Konvertierung von Binärzahlen in Dezimalzahlen werden hier nicht besprochen .
In Java sind mehrere Methoden integriert, die uns bei der Konvertierung verschiedener Basen helfen. Wie in der folgenden Abbildung gezeigt (am Beispiel der Ganzzahlformung, sind andere Typen gleich):
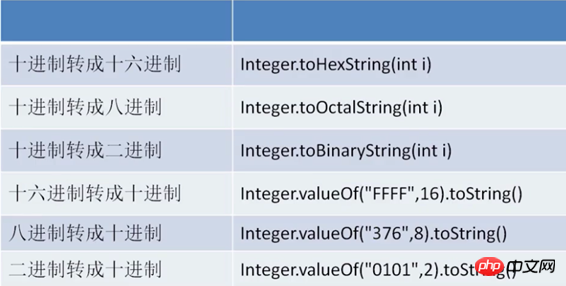
1, Dezimalzahl in andere Basen umwandeln:
1 二进制:Integer.toHexString(int i);2 八进制:Integer.toOctalString(int i);3 十六进制:Integer.toBinaryString(int i);
2. Konvertieren Sie andere Basen in Dezimalzahlen:
1 二进制:Integer.valueOf("0101",2).toString;2 八进制:Integer.valueOf("376",8).toString;3 十六进制:Integer.valueOf("FFFF",16).toString;
3. Verwenden Sie die Methoden parseInt() und valueOf() in der Integer-Klasse, um andere Basen zu konvertieren in Dezimalzahl.
Der Unterschied besteht darin, dass der Rückgabewert der parseInt()-Methode vom Typ int ist, während der Rückgabewert von valueOf() ein Integer-Objekt ist.
2. Grundlegende Bitoperationen
Binär kann genau wie Dezimalzahlen addieren, subtrahieren, multiplizieren und dividieren, verfügt aber auch über eine einfachere Operationsmethode – Bitoperationen. Beispielsweise beträgt die Größe des int-Typs in Computern 32 Bit, was durch 32-Bit-Binärzahlen dargestellt werden kann, sodass wir Bitoperationen verwenden können, um int-Typwerte zu berechnen. Natürlich können Sie einige auch mit gewöhnlichen Methoden berechnen Daten, hier stelle ich Ihnen hauptsächlich die Methoden der Bitoperation vor. Wir werden feststellen, dass Bitoperationen eine mit gewöhnlichen Operationsmethoden unvergleichliche Leistungsfähigkeit haben. Weitere Anwendungen von Bit-Operationen finden Sie in meinem nächsten Blogbeitrag „Magische Bit-Operationen“
Werfen wir zunächst einen Blick auf die Grundlagen Operatoren von Bitoperationen:
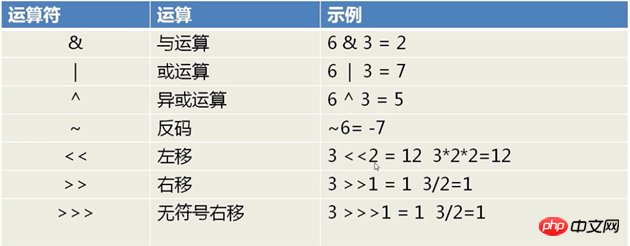
Vorteile:
Unter bestimmten Umständen einfache Berechnung, schnelle Geschwindigkeit, breite Unterstützung
Wenn Sie arithmetische Methoden verwenden, ist die Geschwindigkeit langsam und die Logik kompliziert
Bitweise Operationen sind nicht auf eine Sprache beschränkt, es handelt sich um die grundlegende Operationsmethode von Computern
>>> > >>>>>>>>>>>>>>>>>>>> > >>>>>>>>>>>>>>>>>>>> >
(1) Bitweise UND &
Wenn beide beiden Bits 1 sind, ist das Ergebnis 1
0&0=0; 0&1= 0;1&0=0;1&1=1
Zum Beispiel: 51&5 ist 0011 0011 & 0000 0101 =0000 0001, also 51&5=1.
Besondere Verwendung
(1)Klar. Wenn Sie eine Einheit auf Null zurücksetzen möchten, auch wenn alle ihre Binärbits 0 sind, verknüpfen Sie sie einfach mit einem UND mit einem Wert, dessen Bits alle Null sind, und das Ergebnis ist Null.
(2) Nehmen Sie die angegebene Position in einer Zahl ein.
Zum Beispiel: Angenommen, X=10101110, nehmen Sie die unteren vier Ziffern von X und verwenden Sie
Methode: Finden Sie eine Zahl, die dem Bit entspricht, das x sein muss. Das entsprechende Bit der Zahl ist 1 und die verbleibenden Bits sind Null. Führen Sie eine UND-Operation für diese Zahl und x durch, um die angegebene Zahl zu erhalten Bit in x.
(2) Bitweises ODER |
Solange einer von ihnen 1 ist, ist das Ergebnis 1.
0|0=0; 1|0=1; 1|1=1;
Zum Beispiel: 51|5 0011 0011 |. 0000 0101 =0011 0111 Daher wird 51|5=55
Sonderverwendung
häufig verwendet, um 1 auf bestimmte Positionen von in Daten zu setzen .
Methode: Suchen Sie eine Zahl, die dem Bit von x entspricht, das auf 1 gesetzt werden soll. Das entsprechende Bit der Zahl ist 1 und die verbleibenden Bits sind Null. Diese Zahl ist relativ zu x oder setzt eine Position in x auf 1.
(3) Exklusives ODER^
Wenn die beiden entsprechenden Bits „exklusiv“ sind (unterschiedliche Werte), dann ist das Ergebnis des Bits 1, andernfalls ist es 0
0^0=0; 1^0=1; 1^1=0;
Zum Beispiel: 51^5 ist 0011 0011 ^ 0000 0101 = 0011 0110 also 51^ 5=54
Besondere Verwendung
(1) ist exklusiv-OR-verknüpft mit 1, dreht eine bestimmte um bit
Methode: Finden Sie eine Zahl, die dem Bit in entspricht
Zum Beispiel: X=1010 1110, drehe die unteren vier Bits von um
(2) Exklusives ODER mit 0, den ursprünglichen Wert beibehalten
Zum Beispiel: >Zwei Variablen tauschen Werte aus
1 . Verwenden Sie die dritte Variable, um
C=A;A=B;B=C;2 zu erreichen. Verwenden Sie Addition und Subtraktion, um den Austausch zweier Variablen zu realisieren A=A+B;B=A-B;A=A-B;3. Verwenden Sie die bitweise XOR-Operation, die auch die effizienteste istPrinzip: Das XOR von eine Zahl ist selbst gleich 0; ^B;A=A^B
(4) Negation und Operation~Invertieren Sie eine Binärzahl bitweise, das heißt, ändern Sie 0 in 1 und 1 in 0
~1=0;~0=1(5) Linksverschiebung<<
Verschiebt alle Binärbits eines Operanden um einen bestimmten Bitbetrag nach links (das Binärbit links wird verworfen und rechts wird 0 hinzugefügt)
Zum Beispiel: 2<<1 =4 10<<1=100
Das High-Bit wird beim Verschieben nach links verworfen. Wenn 1 nicht enthalten ist, entspricht jede Verschiebung nach links einer Multiplikation der Zahl mit 2.Zum Beispiel:
11(1011)<<2= 0010 1100=22
11(00000000 00000000 00000000 1011) 32bit Alle Binärziffern einer Zahl um eine bestimmte Anzahl von Stellen nach rechts verschieben, links mit 0 auffüllen für positive Zahlen, links auffüllen mit 1 für negative Zahlen und verwerfen Sie das rechte . Wenn das höherwertige Bit beim Verschieben nach rechts nicht 1 ist (dh es ist keine negative Zahl), entspricht dies jeder Verschiebung des Operanden nach rechts einer Division der Zahl durch 2. Linksauffüllung mit 0 oder Auffüllung mit 1 hängt davon ab, ob die verschobene Zahl positiv oder negativ ist. Zum Beispiel: 4>>2=4/2/2=1 -14 (d. h. 1111 0010)>>2 =1111 1100=-4 Verschiebt jedes Bit um die angegebene Anzahl von Stellen nach rechts,Nach der Rechtsverschiebung werden die frei gewordenen Bits nach links verschoben mit Nullen gefüllt sind, entfernen Sie das rechte Bit und verwerfen Sie es. Zum Beispiel: -14>>>2 (d. h. 11111111 11111111 11111111 11110010)>>>2 = (00111111 11111111 11111111 11111100)=1073741820 >>>>>>>>>> ;> > ;>>>>>>>>>>>>>>>>>>>>>>>> > ;>>>>>>>>>>>>>>>>> oben erwähnt Die binäre Bitdarstellung einer negativen Zahl unterscheidet sich geringfügig von der einer positiven Zahl, daher unterscheidet sich auch die bitweise Operation von der einer positiven Zahl. Eine negative Zahl wird in ihrer Komplementform als positive Zahl ausgedrückt! Nehmen Sie das oben erwähnte -14 als Beispiel, um den Originalcode, den Umkehrcode und den Komplementcode kurz zu erläutern. Originalcode Eine gemäß ihrem Absolutwert aus einer Ganzzahl umgewandelte Binärzahl wird als Originalcode bezeichnet Für Beispiel: 00000000 00000000 00000000 00001110 ist der ursprüngliche Code von 14. Umkehrcode Kehren Sie die Binärzahl Stück für Stück um, und die resultierende neue Binärzahl wird als Umkehrung des Originals bezeichnet binärer Zahlencode. Zum Beispiel: Negiere jedes Bit von 00000000 00000000 00000000 00001110, erhält 11111111 11111111 11111111. 1111 0001 Hinweis: Diese beiden ergänzen einander Komplementärcode Das Komplement plus 1 heißt Komplement 11111111 11111111 11110001 +1= 11111111 11111111 11111111 11110010 Jetzt erhalten wir die binäre Darstellung von -14, verschieben Sie sie nun um -14 nach links (11111111 11111111 11111111 11110010)<<2 = 11111111 11111111 11111111 11001000 =? Analyse: Das erste Bit dieser Binärzahl ist 1, was bedeutet, dass es in Zweierkomplementform vorliegt. Jetzt müssen wir den Zweierkomplementcode in den Originalcode (seinen positiven Wert) umwandeln und den Originalcode in den Komplementcode umwandeln. Im Gegenteil, die Schritte zum Konvertieren des Komplementcodes in den Originalcode: Der Komplementcode wird um 1 subtrahiert, um den Komplementcode zu erhalten : (11000111) Die ersten 24 Bits sind 1 und Kehren Sie den Code um, um den ursprünglichen Code zu erhalten (d. h. den positiven Wert der negativen Zahl) (00111000) Berechnen Sie den positiven Wert, der positive Wert ist 56 Nehmen Sie das Gegenteil des positiven Werts und erhalten Sie das Ergebnis -56 Schlussfolgerung: -14<<2 = -56 Werden Binärdateien in Java häufig verwendet? In der täglichen Entwicklung werden „Basiskonvertierung“ und „Bitoperationen“ nicht häufig verwendet. Java übernimmt Aufgaben auf hoher Ebene. wird häufig plattformübergreifend verwendet, z. B. beim Lesen und Schreiben von Dateien sowie bei der Datenkommunikation. Sehen wir uns ein Szenario an: Wenn sowohl der Client als auch der Server in Java geschriebene Programme sind, senden wir dann Objektdaten, wenn der Client Objektdaten sendet Die zu sendenden Daten können in serialisierbar umgewandelt werden. Nachdem der Server die serialisierten Daten erhalten hat, kann er sie deserialisieren und die darin enthaltenen Objektdaten auslesen. Da die Anzahl der Client-Besuche zunimmt, berücksichtigen wir nicht die Leistung des Servers. Tatsächlich besteht eine praktikable Lösung darin, die Java-Sprache des Servers in die C-Sprache zu ändern. Die C-Sprache als zugrunde liegende Sprache hat eine schnellere Antwortgeschwindigkeit als die Java-Sprache. Wenn der Client zu diesem Zeitpunkt serialisierte Daten übergibt, kann die C-Sprache auf der Serverseite diese nicht analysieren soll ich das tun? Wir können die Daten in binär (0,1) konvertieren, damit der Server diese Sprachen analysieren kann. >>>>>>>>>>>>> ;>> ;>>>>>>>>>>>>>>>>>>>>>>> ;>> ;>>>>>>>>>>>> Grundlegende Datentypen in JavaEs gibt die folgenden vier Typen: Int-Datentyp: Byte (8 Bit, -128 ~ 127), kurz (16 Bit), int (32 Bit), lang (64 Bit) Float-Datentyp: einfache Genauigkeit (Float, 32 Bit), doppelte Genauigkeit (doppelt, 64 Bit) Die Werte von Variablen vom Typ Boolesch sind wahr und falsch (Beide sind 1 Bit) char-Datentyp: Unicode-Zeichen, 16 Bit Entsprechender Klassentyp: Ganzzahl, Float, Boolean, Zeichen, Double, Short, Byte, Long ;>>>>>>>>>>>>>>>>>> >>>>>>> ;>>>>>>>>>>>>>>>> (1) Datentyp In Bytes konvertierenZum Beispiel: int type 8143 (00000000 00000000 00011111 11001111) Erstes (unteres Ende) Byte: 8143>>0*8 & 0xff=(11001111)=207 (oder mit Vorzeichen -49) Zweites ( unteres Ende) Byte: 8143> ;>1*8 &0xff=(00011111)=31 Drittes (unteres Ende) Byte: 8143>>2*8 &0xff=00000000=0 Viertes (unteres Ende) Bytes: 8143>>3*8 &0xff=00000000=0 Uns ist aufgefallen, dass das Obige (unteres Ende) von rechts nach links beginnt, also Was? Ist es Low-End? Lassen Sie es uns aus der Perspektive von Big und Small Endian erklären. Die Low--Bytes werden am -Adressende des Speichers angeordnet Von diesem Wert wird das High-Byte am High-Adressende des SpeichersBig-Endian eingestuft Das High-Byte wird am -Adressende des Speichers angeordnet, das die Startadresse des Werts darstellt, und das Low-Byte wird im hoch Adresse Ende des Speichers Warum gibt es Big- und Small-Endian-Modi? C-Sprache Zum Beispiel: 32-Bit-Zahl 0x12 34 56 78 (hexadezimal) Die Speichermethode der CPU im Big-Endian-Modus (vorausgesetzt, sie beginnt bei Adresse 0x4000) ist 0x4001 0x4002 0x4003 存放内容 0x78 0x56 0x34 0x12 在Little-Endian模式CPU的存放方式(假设从地址0x4000开始存放)为 内存地址 0x4000 0x4001 0x4002 0x4003 存放内容 0x12 0x34 0x56 0x78 1.字符串->字节数组 2.字节数组->字符串 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 两种类型转化为字节的方法都介绍了,下面写个小例子检验一下: 运行结果: 结束语:最近偷懒了,没有好好学习,好几天没写文了,哎,还请大家多多监督! Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Binär- und Bitoperationen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website! (6) Rechtsverschiebung>>
(7) Vorzeichenlose Rechtsverschiebungsoperation>>>
Drei, Basisarithmetik in Java
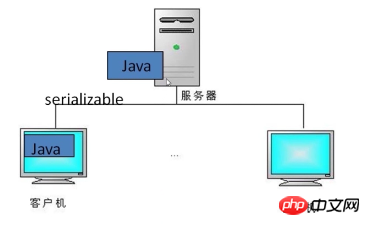
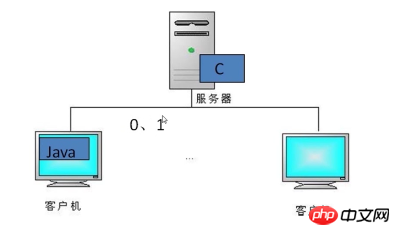
=>byte[] b=[- 49,31,0,0]
0x4000
(二)字符串转化为字节
1 String s;2 byte[] bs=s.getBytes();
1 Byte[] bs=new byte[int];2 String s =new String(bs);或3 String s=new String(bs,encode);//encode指编码方式,如utf-8
1 public class BtyeTest { 2 /* 3 * int整型转为byte字节 4 */ 5 public static byte[] intTOBtyes(int in){ 6 byte[] arr=new byte[4]; 7 for(int i=0;i<4;i++){ 8 arr[i]=(byte)((in>>8*i) & 0xff); 9 }10 return arr;11 }12 /*13 * byte字节转为int整型14 */15 public static int bytesToInt(byte[] arr){16 int sum=0;17 for(int i=0;i<arr.length;i++){18 sum+=(int)(arr[i]&0xff)<<8*i;19 }20 return sum;21 }22 public static void main(String[] args) {23 // TODO Auto-generated method stub24 byte[] arr=intTOBtyes(8143);25 for(byte b:arr){26 System.out.print(b+" ");27 }28 System.out.println();29 System.out.println(bytesToInt(arr));30 31 //字符串与字节数组32 String str="云开的立夏de博客园";33 byte[] barr=str.getBytes();34 35 String str2=new String(barr);36 System.out.println("字符串转为字节数组:");37 for(byte b:barr){38 System.out.print(b+" ");39 40 }41 System.out.println();42 43 System.out.println("字节数组换位字符串:"+str2);44 45 46 }47 48 }


