Heim >Java >javaLernprogramm >Tutorial zur Verwendung des SPFA-Algorithmus
Tutorial zur Verwendung des SPFA-Algorithmus
- 巴扎黑Original
- 2017-07-20 10:23:051586Durchsuche
Anwendungsbereich: Es gibt negative Gewichtskanten in einem bestimmten Diagramm. Derzeit können Algorithmen wie Dijkstra nicht verwendet werden, und die Komplexität des Bellman-Ford-Algorithmus ist zu hoch, so der SPFA Der Algorithmus ist praktisch. Wir sind uns einig, dass es im gerichteten gewichteten Graphen G keinen negativen Gewichtszyklus gibt, das heißt, der kürzeste Weg muss existieren. Natürlich können wir vor der Ausführung des Algorithmus eine topologische Sortierung durchführen, um festzustellen, ob ein negativer Gewichtszyklus vorliegt, aber dies ist nicht der Schwerpunkt unserer Diskussion.
Algorithmusidee: Wir verwenden Array d, um die Schätzung des kürzesten Pfads jedes Knotens aufzuzeichnen, und verwenden eine Adjazenzliste, um Diagramm G zu speichern. Die Methode, die wir anwenden, ist die dynamische Näherungsmethode: Richten Sie eine First-In-First-Out-Warteschlange ein, um die zu optimierenden Knoten zu speichern. Während der Optimierung nehmen wir jedes Mal den Kopfknoten u heraus und verwenden die aktuelle Schätzung des kürzesten Pfads Punkt u, um Punkt u zu verlassen. Der Knoten v, auf den gezeigt wird, wird einer Entspannungsoperation unterzogen. Wenn die kürzeste Pfadschätzung von Punkt v angepasst wird und sich Punkt v nicht in der aktuellen Warteschlange befindet, wird Punkt v am Ende der Warteschlange platziert. Auf diese Weise werden Knoten kontinuierlich aus der Warteschlange entfernt, um Entspannungsoperationen durchzuführen, bis die Warteschlange leer ist
Die erwartete Zeitkomplexität beträgt O(ke) , wobei k die durchschnittliche Häufigkeit ist, mit der alle Scheitelpunkte dem Team beitreten. Es kann bewiesen werden, dass k im Allgemeinen kleiner oder gleich 2 ist.
Implementierungsmethode:
Zunächst gibt es nur den Start Punkt in der Warteschlange und erstellen Sie dann eine Tabelle, um den kürzesten Pfad vom Startpunkt zu allen Punkten aufzuzeichnen (der Anfangswert der Tabelle sollte dem Maximalwert zugewiesen werden, und der Pfad vom Punkt zu sich selbst sollte zugewiesen werden 0). Führen Sie dann eine Entspannungsoperation durch und verwenden Sie dabei einige Punkte in der Warteschlange als Ausgangspunkt, um den kürzesten Weg zu allen Punkten zu aktualisieren. Wenn die Aktualisierung erfolgreich ist und sich der aktualisierte Punkt nicht in der Warteschlange befindet, wird der Punkt am Ende der Warteschlange hinzugefügt . Wiederholen, bis die Warteschlange leer ist.
Bestimmen Sie, ob eine negative Schleife vorhanden ist:
Wenn ein Punkt mehr als N-mal in die Warteschlange gelangt, liegt eine negative Schleife vor (SPFA kann nicht mit Negativschleifen umgehen). Schleifen Bild)
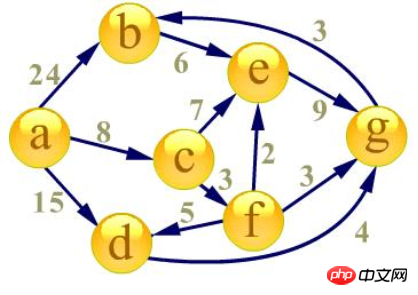
Ermitteln Sie zunächst die kürzeste Entfernung vom Startpunkt a zu den restlichen Punkten
Pfadtabelle
> 1. Das erste Element (a) des Teams wird aus der Warteschlange entfernt und die Entspannungsoperation wird an den Endpunkten aller Kanten mit a als durchgeführt Ausgangspunkt (hier gibt es drei Punkte b, c und d). Zu diesem Zeitpunkt ist der Status der Pfadtabelle: 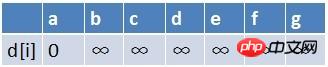
Klicken Sie auf
, um beizutreten Zu diesem Zeitpunkt werden drei neue Knoten b, c und d zur Warteschlange hinzugefügt.
Das erste Element des Teams, Punkt b, wird aus der Warteschlange entfernt an den Endpunkten aller Kanten mit b als Startpunkt in der Reihenfolge (hier gibt es nur Punkt e). Zu diesem Zeitpunkt lautet der Pfadtabellenstatus: 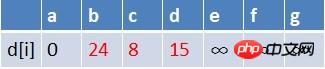
In der kürzesten Pfadtabelle ist auch die kürzeste Pfadschätzung von e nicht in der Warteschlange vorhanden, daher muss e auch
sein Treten Sie der Warteschlange bei. Zu diesem Zeitpunkt sind die Elemente in der Warteschlange c, d, e
Das Kopfelement der Warteschlange wird am Punkt c entfernt und die Endpunkte aller Kanten beginnen Von c werden nacheinander entspannt (hier sind e, f zwei Punkte), zu diesem Zeitpunkt ist der Status der Pfadtabelle: In der kürzesten Pfadtabelle ist die minimale Pfadbewertung von E, f kleiner geworden, E existiert in der Warteschlange, F existiert nicht. Daher muss Das erste Element des Teams ist Punkt d. Verlassen Sie die Warteschlange und führen Sie Entspannungsoperationen an den Endpunkten aller Kanten aus, beginnend mit d (hier gibt es nur Punkt g). Zu diesem Zeitpunkt lautet der Pfadtabellenstatus: . (Entspannung ist erfolglos), kein neuer Knoten kommt in die Warteschlange, das Element in der Warteschlange ist f, g Das Kopfelement des Teams f zeigt aus der Warteschlange, für alle Kanten mit f als Startpunkt. Die Entspannungsoperation wird nacheinander am Endpunkt (dort) ausgeführt sind hier drei Punkte d, e und g). Die Schätzungen für den kürzesten Weg von e und g werden wieder kleiner. Es gibt keinen Punkt e in der Warteschlange, und e tritt der Warteschlange bei. Zu diesem Zeitpunkt muss der Punkt g nicht hinzugefügt werden queue Das Element ist g, e Es gibt keinen Punkt b, b kommt zu diesem Zeitpunkt in die Warteschlange. Das Element in der Warteschlange ist e, b Das erste Element des Teams, Punkt e, verlässt die Warteschlange und die Endpunkte aller Kanten mit e als Startpunkt werden nacheinander entspannt ( Hier gibt es nur Punkt g). > In der kürzesten Pfadtabelle hat sich die Schätzung des kürzesten Pfads von g nicht geändert (die Entspannung war nicht erfolgreich. Zu diesem Zeitpunkt ist das Element in der Warteschlange b In der kürzesten Pfadtabelle hat sich die Schätzung des kürzesten Pfades von e nicht geändert (die Entspannung war erfolglos) und die Warteschlange ist zu diesem Zeitpunkt leer Endlich kommt a an. Der kürzeste Weg von g ist 14 Java-Code 

e nicht in die Warteschlange aufgenommen werden, f jedoch schon. Zu diesem Zeitpunkt sind die Elemente in der Warteschlange d, e, f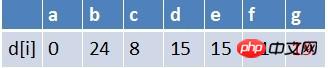
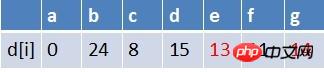 Das erste Element der Warteschlange wird am Punkt b aus der Warteschlange entfernt. Führen Sie Entspannungsoperationen an den Endpunkten aller Kanten mit b als Startpunkt durch (hier gibt es nur Punkt e. Zu diesem Zeitpunkt lautet der Pfadtabellenstatus:
Das erste Element der Warteschlange wird am Punkt b aus der Warteschlange entfernt. Führen Sie Entspannungsoperationen an den Endpunkten aller Kanten mit b als Startpunkt durch (hier gibt es nur Punkt e. Zu diesem Zeitpunkt lautet der Pfadtabellenstatus: 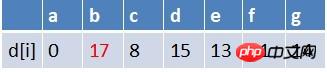
Das obige ist der detaillierte Inhalt vonTutorial zur Verwendung des SPFA-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

