Heim >Backend-Entwicklung >Python-Tutorial >Teilen Sie häufig verwendete Sortierbeispiele in Python
Teilen Sie häufig verwendete Sortierbeispiele in Python
- PHP中文网Original
- 2017-06-21 16:40:361460Durchsuche
Stabilität und Bedeutung des Sortieralgorithmus
Blasensortierung
Komplexität und Stabilitätseigenschaften
Auswahlsortierung
Einfügungssortierung
-
Hügelsortierung
Schnellsortierung
Vergleich der Effizienz gängiger Sortieralgorithmen
Stabilität und Bedeutung von Sortieralgorithmen
In der zu sortierenden Reihenfolge gibt es Datensätze mit denselben Schlüsselwörtern, und die relative Reihenfolge dieser Datensätze bleibt nach dem Sortieren unverändert, sodass der Sortieralgorithmus stabil ist.
Eine instabile Sortierung kann die Sortierung mehrerer Schlüsselwörter nicht abschließen. Bei der Ganzzahlsortierung gilt beispielsweise: Je höher die Anzahl der Ziffern, desto höher die Priorität, d. h. die Sortierung erfolgt von hohen Ziffern zu niedrigen Ziffern. Dann erfordert die Sortierung jedes Bits einen stabilen Algorithmus, da sonst nicht das richtige Ergebnis erzielt werden kann.
Das heißt, Wenn mehrere Schlüsselwörter mehrfach sortiert werden sollen, muss ein stabiler Algorithmus verwendet werden
Blasensortierung
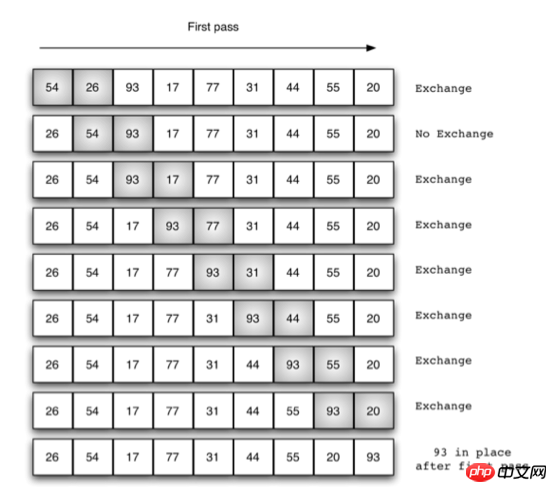 

def bubble_sort(alist):
"""
冒泡排序
"""
if len(alist) <= 1:
return alist
for j in range(len(alist)-1,0,-1):
for i in range(j):
if alist[i] > alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
return alist
Komplexität und Stabilität
Optimale zeitliche Komplexität: (O(n)) Die Durchquerung findet keine Elemente, die ausgetauscht werden können, und die Sortierung endet
Schlechteste Zeitkomplexität: (O(n^2))
Stabilität: Stabil
Auswahlsortierung
Auswahlsortierung ist ein einfacher und intuitiver Sortieralgorithmus. So funktioniert es. Suchen Sie zunächst das kleinste (große) Element in der unsortierten Sequenz und speichern Sie es am Anfang der sortierten Sequenz. Suchen Sie dann weiterhin das kleinste (große) Element aus den verbleibenden unsortierten Elementen und fügen Sie es dann am Ende der sortierten Sequenz ein sortierte Reihenfolge. Und so weiter, bis alle Elemente sortiert sind.
Einfügesortierung
Einfügesortierung erstellt eine geordnete Sequenz. Scannen Sie bei unsortierten Daten die sortierte Sequenz von hinten nach vorne, um die entsprechende Position zu finden und einzufügen. Bei der Implementierung der Einfügungssortierung müssen die sortierten Elemente während des Scanvorgangs von hinten nach vorne wiederholt und schrittweise nach hinten verschoben werden, um Einfügungsraum für die neuesten Elemente zu schaffen.
 

def insert_sort(alist):
"""
插入排序
"""
n = len(alist)
if n <= 1:
return alist
# 从第二个位置,即下表为1的元素开始向前插入
for i in range(1, n):
j = i
# 向前向前比较,如果小于前一个元素,交换两个元素
while alist[j] < alist[j-1] and j > 0:
alist[j], alist[j-1] = alist[j-1], alist[j]
j-=1
return alist
Komplexität und Stabilität
Optimale zeitliche Komplexität: O((n)) (aufsteigende Anordnung, die Reihenfolge ist bereits in aufsteigender Reihenfolge)
Schlechteste Zeitkomplexität: O((n^2))
Stabilität: Stabil
Shell Sort
Shell Sort ist eine Verbesserung der Einfügungssortierung und die Sortierung ist nicht stabil. Bei der Hill-Sortierung werden Datensätze nach einem bestimmten Inkrement des Indexes gruppiert und jede Gruppe mithilfe des Direkteinfügungssortieralgorithmus sortiert. Mit zunehmender Inkrementierung enthält jede Gruppe immer mehr Schlüsselwörter auf 1 reduziert, die gesamte Datei in eine Gruppe aufgeteilt und der Algorithmus beendet.
def shell_sort(alist): n = len(alist) gap = n//2 # gap 变化到0之前,插入算法之行的次数 while gap > 0: # 希尔排序, 与普通的插入算法的区别就是gap步长 for i in range(gap,n): j = i while alist[j] < alist[j-gap] and j > 0: alist[j], alist[j-gap] = alist[j-gap], alist[j] j-=gap gap = gap//2 return alist
Komplexität und Stabilität
Optimale zeitliche Komplexität: (O(n^{1.3})) (muss nicht bestellt werden)
Schlechteste Zeitkomplexität: (O(n^2))
Stabilität: instabil
Schnellsortierung
Quicksort (Quicksort) teilt die zu sortierenden Daten in einem Sortierdurchgang in zwei unabhängige Teile auf. Alle Daten in einem Teil sind kleiner als alle Daten im anderen Teil. Anschließend wird diese Methode zum schnellen Sortieren verwendet Die beiden Teile der Daten können jeweils rekursiv sortiert werden, sodass die gesamten Daten zu einer geordneten Sequenz werden.
Die Schritte sind:
Wählen Sie ein Element aus der Sequenz aus, das als „Pivot“ bezeichnet wird.
Re In a Sortierte Reihenfolge: Alle Elemente, die kleiner als der Basiswert sind, werden vor der Basis platziert, und alle Elemente, die größer als der Basiswert sind, werden hinter der Basis platziert (auf beiden Seiten kann die gleiche Zahl stehen). Nach dieser Partition befindet sich das Datum in der Mitte der Sequenz. Dies wird als Partitionsvorgang bezeichnet.
Sortieren Sie rekursiv das Subarray der Elemente, die kleiner als der Basiswert sind, und das Subarray der Elemente, die größer als der Basiswert sind.
Der unterste Fall der Rekursion liegt vor, wenn die Größe der Sequenz Null oder Eins ist, das heißt, sie wurde immer sortiert. Obwohl er weiterhin rekursiv ist, wird dieser Algorithmus immer enden, da er in jeder Iteration (Iteration) mindestens ein Element an seine endgültige Position bringt.
Vergleich der Effizienz gängiger Sortieralgorithmen
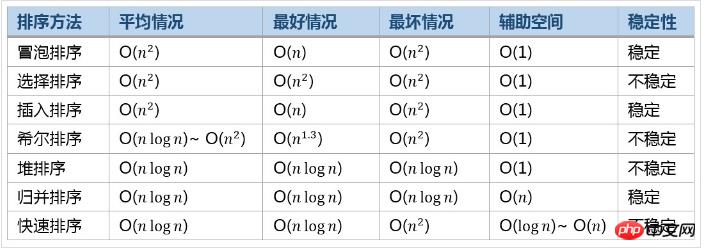 

Das obige ist der detaillierte Inhalt vonTeilen Sie häufig verwendete Sortierbeispiele in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

