Detaillierte Erläuterung der Beispiele für Tiefen- und Breitenalgorithmen

Lassen Sie mich zunächst den zweiten Teil der Algorithms-Website vorstellen, den Online-Kurs des Buches Algorithmen.

Darüber hinaus ist der Kurs zu Graphalgorithmen auf Coursera auch sehr gut.

Mehrere Darstellungsmethoden von Diagrammen:

Auf diese Weise wird (Datenstruktur) dargestellt das Diagramm, das die folgenden zwei Anforderungen beinhaltet: (1) Der Platz muss angemessen sein (2) Die Implementierung der Instanzmethode muss schnell sein

Dann stehen drei Optionen zur Auswahl :

(1) Die Kantenmenge ist wie folgt:

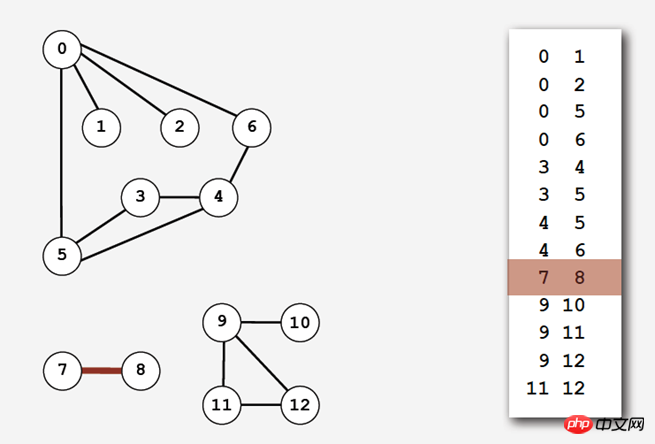
Einfach, erfüllt jedoch nicht die beiden Bedingungen: Um die Adjazenzliste adj() zu implementieren, müssen alle Kanten im Diagramm durchlaufen werden.

(2) Adjazenzmatrix:

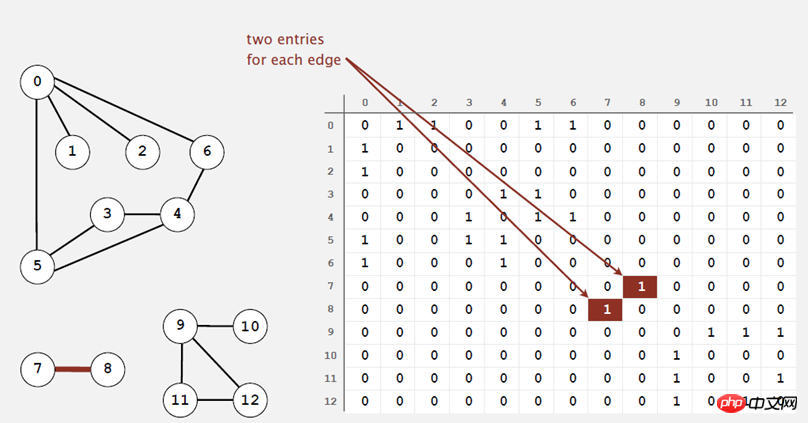
Verwenden Sie ein V mal V Der Boolesche Beweis ist im Raum nicht erfüllt.

(3) Adjazenzliste:

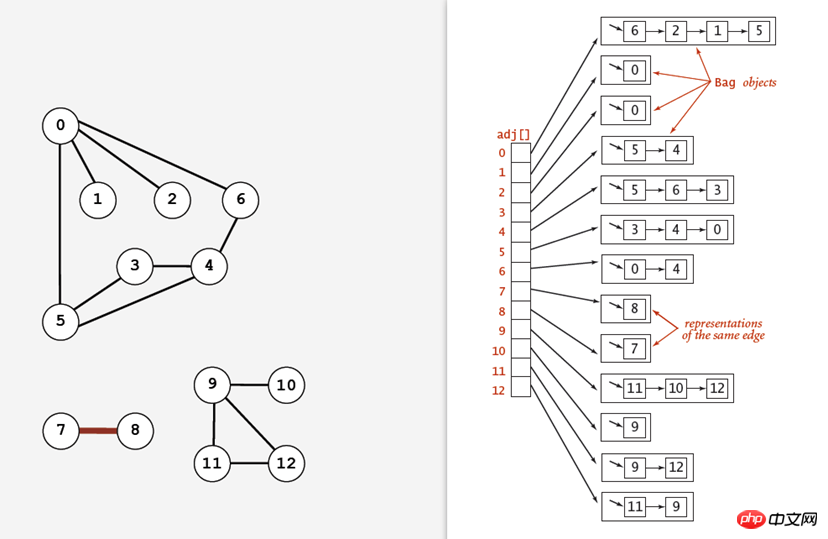
Verwenden Sie einen Scheitelpunkt als index Eine Array-Liste, bei der jedes Element eine Liste von Scheitelpunkten neben dem Scheitelpunkt ist.

Da die obige Methode eine größere Flexibilität bietet und zur Darstellung eine Adjazenzliste verwendet wird, kann die folgende Datenstruktur zur Darstellung eines Graph-Objekts definiert werden.

public class Graph
{private readonly int verticals;//顶点个数private int edges;//边的个数private List<int>[] adjacency;//顶点联接列表public Graph(int vertical)
    {this.verticals = vertical;this.edges = 0;
        adjacency=new List<int>[vertical];for (int v = 0; v < vertical; v++)
        {
            adjacency[v]=new List<int>();
        }
    }public int GetVerticals ()
    {return verticals;
    }public int GetEdges()
    {return edges;
    }public void AddEdge(int verticalStart, int verticalEnd)
    {
        adjacency[verticalStart].Add(verticalEnd);
        adjacency[verticalEnd].Add(verticalStart);
        edges++;
    }public List<int> GetAdjacency(int vetical)
    {return adjacency[vetical];
    }
}

Depth-First-Algorithmus

Bevor wir über den Depth-First-Algorithmus sprechen, können wir zunächst einen Blick darauf werfen bei der Labyrinth-Erkundungsfrage. Das Folgende ist die Entsprechung zwischen einem Labyrinth und einem Diagramm:

Jeder Schnittpunkt im Labyrinth stellt einen Scheitelpunkt im Diagramm dar, und jeder Kanal entspricht einer Kante.

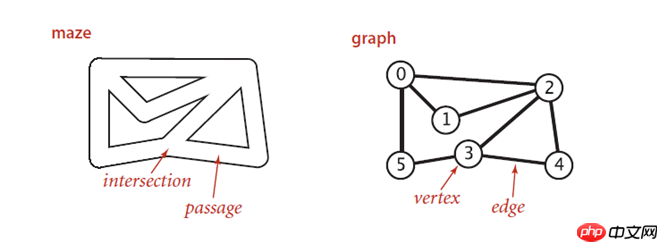
Die Trémaux-Seilerkundungsmethode kann zur Erkundung des Labyrinths verwendet werden. Das heißt:

• Legen Sie ein Seil hinter sich

• Legen Sie es überall hin Besuch Ein Seil markiert die besuchten Kreuzungspunkte und Passagen

• Wenn Sie auf einen besuchten Ort stoßen, gehen Sie am Seil entlang zurück zu einem Ort, der noch nicht besucht wurde vorher:

Das Symbol sieht wie folgt aus:

unten Es ist eine kleine Animation der Labyrintherkundung:

Der Tiefensuchalgorithmus simuliert die Labyrintherkundung. In tatsächlichen Diagrammverarbeitungsalgorithmen trennen wir normalerweise die Darstellung des Diagramms und die Verarbeitungslogik des Diagramms. Das allgemeine Entwurfsmuster des Algorithmus lautet also wie folgt:

• Erstellen Sie ein Diagrammobjekt

• Diagramm erstellen Das Objekt wird an das Verarbeitungsobjekt des Diagrammalgorithmus übergeben, z. B. ein Pfadobjekt

• , und dann werden die verarbeiteten Ergebnisse abgefragt, um Informationen zu erhalten

Wir können sehen, dass beim rekursiven Aufruf der dfs-Methode ein markiertes[]-Tag-Array verwaltet, um festzustellen, ob der Knoten vor dem Aufruf von besucht wurde .

Beschreibung des Tiefen-First-Algorithmus: Beim Besuch eines Scheitelpunkts

1. Markieren Sie ihn als besucht;

2. Besuchen Sie rekursiv alle nicht markierten Nachbarscheitelpunkte.

public class DepthFirstSearch
{private bool[] marked;//记录顶点是否被标记private int count;//记录查找次数private DepthFirstSearch(Graph g, int v)
    {
        marked = new bool[g.GetVerticals()];
        dfs(g, v);
    }private void dfs(Graph g, int v)
    {
        marked[v] = true;
        count++;foreach (int vertical in g.GetAdjacency(v))
        {if (!marked[vertical])
                dfs(g,vertical);
        }
    }public bool IsMarked(int vertical)
    {return marked[vertical];
    }public int Count()
    {return count;
    }
}

试验一个算法最简单的办法是找一个简单的例子来实现。

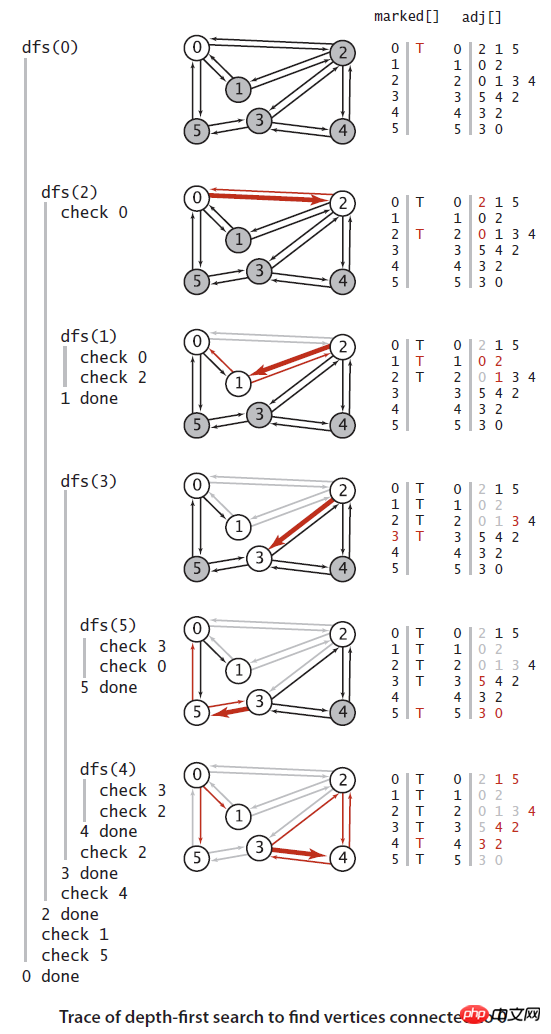
算法应用：

连通性。给定一幅图，回答“两个给定顶点是否连通？” 或者 “图中有多少个连通子图？”

寻找路径。给定一幅图和一个起点，回答“从s到给定目的顶点v是否存在一条路径？如果有，找出这条路径。”

检测环。给定的图是无环图吗？

双色问题。能够用两种颜色将图的所有顶点着色，使得任意一条边连个顶点的颜色都不相同？这个问题等价于：这是一个二分图吗？

 

深度优先路径查询

有了这个基础，我们可以实现基于深度优先的路径查询，要实现路径查询，我们必须定义一个变量来记录所探索到的路径。

所以在上面的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录，和仅记录从当前节点到起始节点不同，我们记录图中的每一个节点到开始节点的路径。为了完成这一日任务，通过设置edgesTo[w]=v，我们记录从v到w的边，换句话说，v-w是做后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。

注意代码只是在前面算法的基础上维护了一个edgTo数组，并用栈Stack保存路径。

public class DepthFirstPaths
{private bool[] marked;//记录是否被dfs访问过
    private int[] edgesTo;//记录最后一个到当前节点的顶点private int s;//搜索的起始点public DepthFirstPaths(Graph g, int s)
    {
        marked = new bool[g.GetVerticals()];
        edgesTo = new int[g.GetVerticals()];this.s = s;
        dfs(g, s);
    }private void dfs(Graph g, int v)
    {
        marked[v] = true;foreach (int w in g.GetAdjacency(v))
        {if (!marked[w])
            {                edgesTo[w] = v;dfs(g,w);
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v){if (!HasPathTo(v)) return null;
        Stack<int> path = new Stack<int>();for (int x = v; x!=s; x=edgesTo[x])
        {
            path.Push(x);
        }
        path.Push(s);return path;
    }
}

 

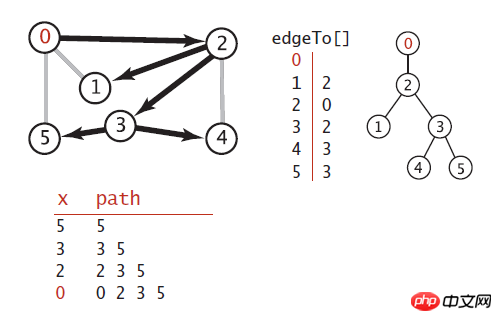
上图中是黑色线条表示 深度优先搜索中，所有定点到原点0的路径， 他是通过edgeTo[]这个变量记录的，可以从右边可以看出，

他其实是一颗树，树根即是原点，每个子节点到树根的路径即是从原点到该子节点的路径。

下图是深度优先搜索算法的一个简单例子的追踪。

 

 

 

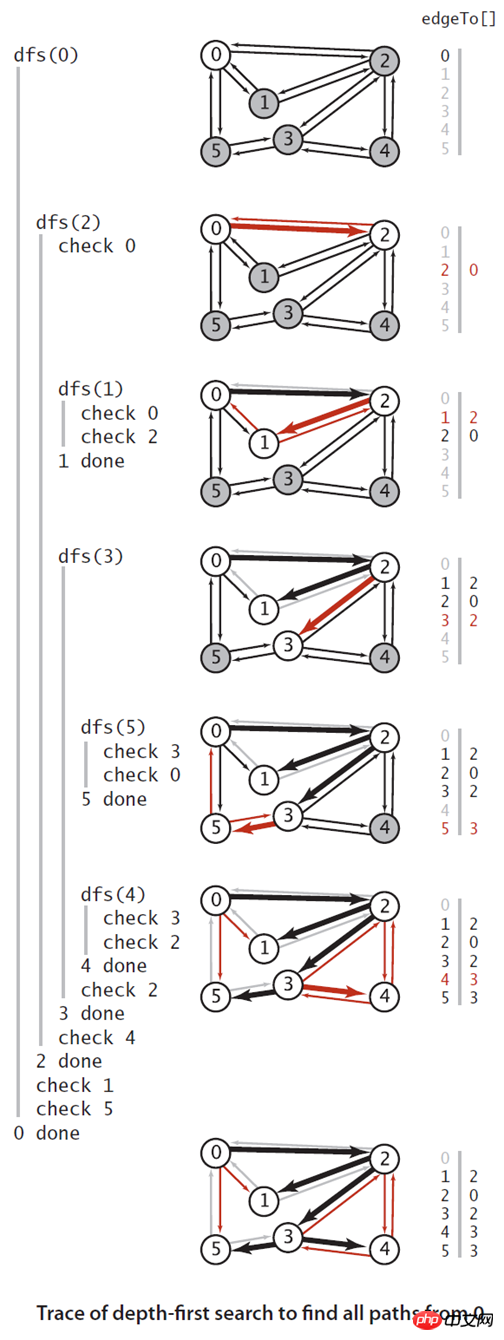
连通分量

API如下：

CC的实现使用了marked[ ]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。递归的深搜第一次调用的参数是顶点0，会标记所有与0连通的顶点。然后构造函数中的for循环会查找每个没有被标记的顶点并递归调用dfs来标记和它相邻的所有顶点。另外，它还使用了一个以顶点作为索引的数组id[ ],将同一个连通分量中的顶点和连通分量的标识符关联起来。这个数组使得connected( )方法的实现变得十分简单。

public class CC {private boolean[] marked;private int[] id;private int count;public CC(Graph g){
        marked = new boolean[g.getVertexCount()];
        id = new int[g.getVertexCount()];for(int s = 0; s < g.getVertexCount(); s++){if(!marked[s]){
                dfs(g,s);
                count++;
            }
        }
    }private void dfs(Graph g, int v) {
        marked[v] = true;
        id[v] = count;for(int w: g.adj(v))if(!marked[w])
                dfs(g,w);
    }/** v和w连通吗*/public boolean connected(int v, int w)    { return id[v] == id[w]; }/** v所在的连通分量的标识符*/public int id(int v)    { return id[v]; }/** 连通分量数*/public int count()        {return count;}

 

检测环

/**
 * 给定的图是无环图吗
 * 检测自环:假设没有自环，没有平行边 */public class Cycle {private boolean[] marked;private boolean hasCycle;public Cycle(Graph g){
        marked = new boolean[g.getVertexCount()];for(int i = 0;i<g.getVertexCount();i++)if(!marked[i])    dfs(g, i, i);
    }private void dfs(Graph g, int v, int u) {
        marked[v] = true;for(int w: g.adj(v))if(!marked[w])    dfs(g, w, v); // 若w没被标记过，那么从w继续递归深搜，把w的父节点作为第二参数else if(w != u) hasCycle = true; // 若w被标记过，那么若无环，w必然和父节点相同，否则就是有环    }/** 是否含有环*/public boolean hasCycle(){return hasCycle;}

 

双色问题

/**
 * 双色问题：能够用两种颜色将图的所有顶点着色，使得任意一条边上的两个端点的颜色都不同吗？
 * 等价于：判断是否是二分图的问题 */public class TwoColor {private boolean[] marked;private boolean[] color;private boolean isColorable;public TwoColor(Graph g){
        isColorable = true;
        marked = new boolean[g.getVertexCount()];
        color = new boolean[g.getVertexCount()];for(int i = 0; i<g.getVertexCount(); i++)//遍历所有顶点if(!marked[i])    dfs(g, i);//没有mark就进行深搜    }private void dfs(Graph g, int v) {
        marked[v] = true;        // 标记for(int w: g.adj(v))    // 对邻接表进行遍历if(!marked[w]){        // 如果没有被标记color[w] = !color[v];    // 当前w节点颜色置为和父节点不同的颜色dfs(g, w);                // 对当前节点继续深搜}else if(color[w] == color[v]){    // 如果已经被标记，看是否颜色和父节点相同isColorable = false;         // 若相同则不是二分图            }
    }/** 是否是二分图*/public boolean isBipartite(){return isColorable;}

 

 

广度优先算法

通常我们更关注的是一类单源最短路径的问题，那就是给定一个图和一个源S，是否存在一条从s到给定定点v的路径，如果存在，找出最短的那条(这里最短定义为边的条数最小)

深度优先算法是将未被访问的节点放到一个堆中(stack)，虽然在上面的代码中没有明确在代码中写stack，但是 递归间接的利用递归堆实现了这一原理。

和深度优先算法不同， 广度优先是将所有未被访问的节点放到了队列中。其主要原理是：

先将起点加入队列，然后重复一下步骤直到队列为空：

1.取队列中的下一个顶点V并标记它

2.将与v相邻的所有未被标记过的顶点加入队列

广度优先是以距离递增的方式来搜索路径的。

class BreadthFirstSearch
{private bool[] marked;private int[] edgeTo;private int sourceVetical;//Source verticalpublic BreadthFirstSearch(Graph g, int s)
    {
        marked=new bool[g.GetVerticals()];
        edgeTo=new int[g.GetVerticals()];this.sourceVetical = s;
        bfs(g, s);
    }private void bfs(Graph g, int s)
    {
        Queue<int> queue = new Queue<int>();
        marked[s] = true;
        queue.Enqueue(s);while (queue.Count()!=0)
        {int v = queue.Dequeue();foreach (int w in g.GetAdjacency(v))
            {if (!marked[w])
                {
                    edgeTo[w] = v;
                    marked[w] = true;
                    queue.Enqueue(w);
                }
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v)
    {if (!HasPathTo(v)) return null;

        Stack<int> path = new Stack<int>();for (int x = v; x!=sourceVetical; x=edgeTo[x])
        {
            path.Push(x);
        }
        path.Push(sourceVetical);return path;
    }

}

算法应用：最短路径问题

 

总结：

深度优先搜索和广度优先搜索都是将起点存入数据结构中，然后重复一下步骤直到数据结构被清空：

1.取其中的下一个顶点并标记它

2.将v的所有相邻而未被标记的顶点加入数据结构

这两个算法 的不同之处仅在于从数据结构中获取下一个顶点的规则（广度优先来说是最早加入的顶点，对于深度优先搜索来说是最晚加入的顶点）。

 

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Beispiele für Tiefen- und Breitenalgorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!