Heim >Backend-Entwicklung >Python-Tutorial >Wie gehe ich mit dünn besetzten Matrizen um? Tutorial zur Python-Implementierung einer Sparse-Matrix
Wie gehe ich mit dünn besetzten Matrizen um? Tutorial zur Python-Implementierung einer Sparse-Matrix
- 零下一度Original
- 2017-06-16 11:08:095589Durchsuche
In diesem Artikel wird hauptsächlich der Beispielcode für die Implementierung einer Sparse-Matrix in Python vorgestellt. Jetzt werde ich ihn mit Ihnen teilen und als Referenz verwenden. Folgen wir dem Herausgeber und werfen wir einen Blick darauf.
In der technischen Praxis sind große Matrizen in den meisten Fällen im Allgemeinen dünn besetzte Matrizen. Daher ist der Umgang mit dünn besetzten Matrizen in der Praxis sehr wichtig. Dieser Artikel nimmt die Implementierung in Python als Beispiel. Lassen Sie uns zunächst untersuchen, wie spärliche Matrizen gespeichert und dargestellt werden.
1. Eine vorläufige Studie zum Sparse-Modul
Im Scipy-Modul in Python gibt es ein Modul namens Sparse-Modul, das speziell für die Lösung von Sparse entwickelt wurde Matrizen. Der Großteil des Inhalts dieses Artikels basiert tatsächlich auf dem Sparse-Modul.
Der erste Schritt besteht darin, das Sparse-Modul zu importieren
>>> from scipy import sparse
und dann zu helfen, schauen wir uns zuerst um
>>> help(sparse)
Finden Sie direkt heraus, was wir sind Am meisten beunruhigt Teil:
Usage information
=================
There are seven available sparse matrix types:
1. csc_matrix: Compressed Sparse Column format
2. csr_matrix: Compressed Sparse Row format
3. bsr_matrix: Block Sparse Row format
4. lil_matrix: List of Lists format
5. dok_matrix: Dictionary of Keys format
6. coo_matrix: COOrdinate format (aka IJV, triplet format)
7. dia_matrix: DIAgonal format
To construct a matrix efficiently, use either dok_matrix or lil_matrix.
The lil_matrix class supports basic slicing and fancy
indexing with a similar syntax to NumPy arrays. As illustrated below,
the COO format may also be used to efficiently construct matrices.
To perform manipulations such as multiplication or inversion, first
convert the matrix to either CSC or CSR format. The lil_matrix format is
row-based, so conversion to CSR is efficient, whereas conversion to CSC
is less so.
All conversions among the CSR, CSC, and COO formats are efficient,
linear-time operations.Durch diese Beschreibung haben wir ein allgemeines Verständnis des Sparse-Moduls. Es gibt 7 Möglichkeiten, Sparse-Matrizen im Sparse-Modul zu speichern. Als nächstes werden wir diese 7 Methoden einzeln vorstellen.
2.coo_matrix
coo_matrix ist die einfachste Speichermethode. Verwenden Sie die drei Arrays row, col und data, um die Informationen von Elementen ungleich Null zu speichern. Die drei Arrays haben die gleiche Länge, row enthält die Zeile der Elemente, col enthält die Spalte der Elemente und data enthält den Wert des Elements. Im Allgemeinen wird coo_matrix hauptsächlich zum Erstellen von Matrizen verwendet, da coo_matrix keine Elemente der Matrix hinzufügen, löschen oder ändern kann. Sobald die Matrix erfolgreich erstellt wurde, wird sie in andere Matrizenformen konvertiert.
>>> row = [2,2,3,2] >>> col = [3,4,2,3] >>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6)) >>> print c.toarray() [[0 0 0 0 0 0] [0 0 0 0 0 0] [0 0 0 5 2 0] [0 0 3 0 0 0] [0 0 0 0 0 0]]
Zu beachten ist, dass bei der Verwendung von coo_matrix zum Erstellen einer Matrix dieselben Zeilen- und Spaltenkoordinaten mehrmals vorkommen können. Nachdem die Matrix tatsächlich erstellt wurde, werden die entsprechenden Koordinatenwerte addiert, um das Endergebnis zu erhalten.
3.dok_matrix und lil_matrix
Das Szenario, in dem dok_matrix und lil_matrix anwendbar sind, besteht darin, schrittweise Elemente der Matrix hinzuzufügen. Die Strategie von doc_matrix besteht darin, ein Wörterbuch zu verwenden, um die Elemente in der Matrix aufzuzeichnen, die nicht 0 sind. Natürlich speichert der Schlüssel des Wörterbuchs die Positionsinformationen des Vorfahren des aufgezeichneten Elements, und der Wert ist der spezifische Wert des aufgezeichneten Elements.
>>> import numpy as np >>> from scipy.sparse import dok_matrix >>> S = dok_matrix((5, 5), dtype=np.float32) >>> for i in range(5): ... for j in range(5): ... S[i, j] = i + j ... >>> print S.toarray() [[ 0. 1. 2. 3. 4.] [ 1. 2. 3. 4. 5.] [ 2. 3. 4. 5. 6.] [ 3. 4. 5. 6. 7.] [ 4. 5. 6. 7. 8.]]
lil_matrix verwendet zwei Listen, um Nicht-Null-Elemente zu speichern. Daten speichert die Nicht-Null-Elemente in jeder Zeile und Zeilen speichert die Spalten, in denen sich die Nicht-Null-Elemente befinden. Dieses Format eignet sich auch hervorragend, um Elemente einzeln hinzuzufügen und schnell zeilenbezogene Daten abzurufen.
>>> from scipy.sparse import lil_matrix >>> l = lil_matrix((6,5)) >>> l[2,3] = 1 >>> l[3,4] = 2 >>> l[3,2] = 3 >>> print l.toarray() [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 1. 0.] [ 0. 0. 3. 0. 2.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]] >>> print l.data [[] [] [1.0] [3.0, 2.0] [] []] >>> print l.rows [[] [] [3] [2, 4] [] []]
Aus der obigen Analyse ist leicht ersichtlich, dass die beiden oben genannten Methoden zum Erstellen dünnbesetzter Matrizen im Allgemeinen verwendet werden, um Matrizen durch schrittweises Hinzufügen von Nicht-Null-Elementen zu erstellen und sie dann in andere Methoden umzuwandeln, die dies können schnell sein Die berechnete Matrixspeichermethode.
4.dia_matrix
Dies ist eine diagonale Speichermethode. Dabei stellen Spalten Diagonalen und Zeilen Zeilen dar. Wenn die Elemente auf der Diagonale alle 0 sind, werden sie weggelassen.
Wenn die ursprüngliche Matrix eine Diagonalmatrix ist, ist die Komprimierungsrate sehr hoch.
Wenn Sie ein Bild im Internet finden, können Sie das Prinzip leicht verstehen.

5.csr_matrix und csc_matrix
csr_matrix, der vollständige Name lautet Compressed Sparse Row, ist zeilenbasiert Verarbeitung von Matrizen komprimiert. CSR erfordert drei Arten von Daten: numerische Werte, Spaltennummern und Zeilenoffsets. CSR ist eine Codierungsmethode, bei der die Bedeutung numerischer Werte und Spaltennummern mit denen in coo übereinstimmt. Der Zeilenoffset gibt die Startoffsetposition des ersten Elements einer Zeile in Werten an.
Ich habe im Internet auch ein Bild gefunden, das das Prinzip besser wiedergeben kann.
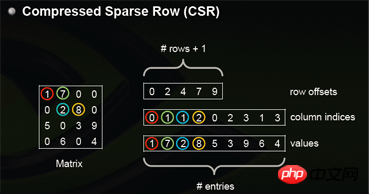
Mal sehen, wie man es in Python verwendet: Wie wäre es mit
>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]]), ist es nicht schwer zu verstehen?
Schauen wir uns an, was im Dokument steht
Notes | ----- | | Sparse matrices can be used in arithmetic operations: they support | addition, subtraction, multiplication, pision, and matrix power. | | Advantages of the CSR format | - efficient arithmetic operations CSR + CSR, CSR * CSR, etc. | - efficient row slicing | - fast matrix vector products | | Disadvantages of the CSR format | - slow column slicing operations (consider CSC) | - changes to the sparsity structure are expensive (consider LIL or DOK)
Es ist nicht schwer zu erkennen, dass csr_matrix besser für echte Matrixoperationen geeignet ist.
csc_matrix ähnelt csr_matrix, ist jedoch basierend auf Spalten komprimiert und wird nicht separat eingeführt.
6.bsr_matrix
Das Block Sparse Row-Format komprimiert, wie der Name schon sagt, die Matrix basierend auf der Idee des Blockierens.

Das obige ist der detaillierte Inhalt vonWie gehe ich mit dünn besetzten Matrizen um? Tutorial zur Python-Implementierung einer Sparse-Matrix. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

