Ausführliche Erläuterung der Implementierung von Binärbäumen und sieben Traversalmethoden in der Python-Programmierung

In diesem Artikel wird hauptsächlich die PythonProgrammierung zur Implementierung von Binärbäumen und sieben Durchlaufmethoden vorgestellt. Außerdem werden die Definition von Python-Binärbäumen und gängige Durchlaufoperationstechniken im Detail analysiert Beispiele. Freunde in Not Sie können sich auf Folgendes beziehen:

Die Beispiele in diesem Artikel beschreiben die Implementierung von Binärbäumen und Traversalmethoden in Python. Teilen Sie es als Referenz mit allen. Die Details lauten wie folgt:

Einführung:

Baum ist eine sehr wichtige Art von Datenstruktur. Sein Hauptzweck wird zur Verbesserung der Sucheffizienz verwendet und ist bei wiederholten Suchvorgängen wie binären Sortierbäumen und FP-Bäumen effektiver. Darüber hinaus kann es zur Verbesserung der Codierungseffizienz verwendet werden, beispielsweise mit dem Huffman-Baum.

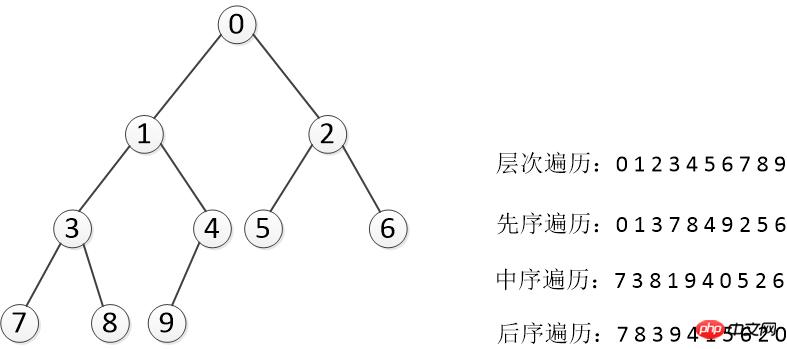
Code:

Verwendung von Python zur Implementierung der Baumkonstruktion und mehrerer Durchlaufalgorithmen, obwohl dies nicht der Fall ist schwierig, aber ich habe den Code trotzdem organisiert und zusammengefasst. Implementierungsfunktionen:

① Baumkonstruktion
② Rekursion Implementieren Sie die Durchquerung vor der Bestellung, die Durchquerung in der Reihenfolge und die Durchquerung nach der Bestellung.
③ Der Stapel implementiert die Durchquerung vor der Bestellung in -Order-Traversal, Post-Order-Traversal
④ Queue implementiert hierarchisches Traversal

#coding=utf-8
class Node(object):
  """节点类"""
  def init(self, elem=-1, lchild=None, rchild=None):
    self.elem = elem
    self.lchild = lchild
    self.rchild = rchild
class Tree(object):
  """树类"""
  def init(self):
    self.root = Node()
    self.myQueue = []
  def add(self, elem):
    """为树添加节点"""
    node = Node(elem)
    if self.root.elem == -1: # 如果树是空的，则对根节点赋值
      self.root = node
      self.myQueue.append(self.root)
    else:
      treeNode = self.myQueue[0] # 此结点的子树还没有齐。
      if treeNode.lchild == None:
        treeNode.lchild = node
        self.myQueue.append(treeNode.lchild)
      else:
        treeNode.rchild = node
        self.myQueue.append(treeNode.rchild)
        self.myQueue.pop(0) # 如果该结点存在右子树，将此结点丢弃。
  def front_digui(self, root):
    """利用递归实现树的先序遍历"""
    if root == None:
      return
    print root.elem,
    self.front_digui(root.lchild)
    self.front_digui(root.rchild)
  def middle_digui(self, root):
    """利用递归实现树的中序遍历"""
    if root == None:
      return
    self.middle_digui(root.lchild)
    print root.elem,
    self.middle_digui(root.rchild)
  def later_digui(self, root):
    """利用递归实现树的后序遍历"""
    if root == None:
      return
    self.later_digui(root.lchild)
    self.later_digui(root.rchild)
    print root.elem,
  def front_stack(self, root):
    """利用堆栈实现树的先序遍历"""
    if root == None:
      return
    myStack = []
    node = root
    while node or myStack:
      while node:           #从根节点开始，一直找它的左子树
        print node.elem,
        myStack.append(node)
        node = node.lchild
      node = myStack.pop()      #while结束表示当前节点node为空，即前一个节点没有左子树了
      node = node.rchild         #开始查看它的右子树
  def middle_stack(self, root):
    """利用堆栈实现树的中序遍历"""
    if root == None:
      return
    myStack = []
    node = root
    while node or myStack:
      while node:           #从根节点开始，一直找它的左子树
        myStack.append(node)
        node = node.lchild
      node = myStack.pop()      #while结束表示当前节点node为空，即前一个节点没有左子树了
      print node.elem,
      node = node.rchild         #开始查看它的右子树
  def later_stack(self, root):
    """利用堆栈实现树的后序遍历"""
    if root == None:
      return
    myStack1 = []
    myStack2 = []
    node = root
    myStack1.append(node)
    while myStack1:          #这个while循环的功能是找出后序遍历的逆序，存在myStack2里面
      node = myStack1.pop()
      if node.lchild:
        myStack1.append(node.lchild)
      if node.rchild:
        myStack1.append(node.rchild)
      myStack2.append(node)
    while myStack2:             #将myStack2中的元素出栈，即为后序遍历次序
      print myStack2.pop().elem,
  def level_queue(self, root):
    """利用队列实现树的层次遍历"""
    if root == None:
      return
    myQueue = []
    node = root
    myQueue.append(node)
    while myQueue:
      node = myQueue.pop(0)
      print node.elem,
      if node.lchild != None:
        myQueue.append(node.lchild)
      if node.rchild != None:
        myQueue.append(node.rchild)
if name == 'main':
  """主函数"""
  elems = range(10)      #生成十个数据作为树节点
  tree = Tree()     #新建一个树对象
  for elem in elems:
    tree.add(elem)      #逐个添加树的节点
  print '队列实现层次遍历:'
  tree.level_queue(tree.root)
  print '\n\n递归实现先序遍历:'
  tree.front_digui(tree.root)
  print '\n递归实现中序遍历:'
  tree.middle_digui(tree.root)
  print '\n递归实现后序遍历:'
  tree.later_digui(tree.root)
  print '\n\n堆栈实现先序遍历:'
  tree.front_stack(tree.root)
  print '\n堆栈实现中序遍历:'
  tree.middle_stack(tree.root)
  print '\n堆栈实现后序遍历:'
  tree.later_stack(tree.root)

Zusammenfassung:

Die Hauptdurchquerung des Baumes Es gibt zwei Arten: Eine ist die Tiefendurchquerung, wie Vorbestellung, Mittelordnung und Nachordnung, die andere ist die Breitendurchquerung, wie hierarchische Durchquerung. Der Unterschied zwischen den beiden ist in der Baumstruktur nicht sehr offensichtlich, aber bei der Erweiterung von einem Baum über einen gerichteten Graphen zu einem ungerichteten Graphen sind die Effizienz und Wirkung der Tiefensuche und der Breitensuche sehr ausgeprägt immer noch sehr toll.

Depth-First verwendet im Allgemeinen Rekursion und Breite-First verwendet im Allgemeinen Warteschlangen. Im Allgemeinen können die meisten Algorithmen, die mithilfe von Rekursion implementiert werden können, auch mithilfe von Stapeln implementiert werden.

Ich habe den Eindruck, dass es eine Möglichkeit gibt, einen Baum rekursiv zu konstruieren, aber ich konnte nie herausfinden, wie man ihn konstruiert. Nach sorgfältiger Überlegung ähnelt rekursives Denken in gewisser Weise dem Tiefenalgorithmus, und die Baumkonstruktion sollte breitenorientiert sein. Wenn Rekursion verwendet wird, muss eine Beendigungsbedingung vorhanden sein, z. B. die Angabe der Baumtiefe usw. Andernfalls wird der konstruierte Baum in Richtung des linken einzelnen Teilbaums oder des rechten einzelnen Teilbaums tendieren. Daher ist es besser, Warteschlangen für den allgemeinen Baumaufbau zu verwenden.

Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung der Implementierung von Binärbäumen und sieben Traversalmethoden in der Python-Programmierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!