Heim >Java >javaLernprogramm >Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
- 黄舟Original
- 2017-03-20 10:37:361734Durchsuche
Der Rot-Schwarz-Baum ist eine Art ausgeglichener binärer Suchbaum. Um Rot-Schwarz-Bäume tiefgreifend zu verstehen, müssen wir mit binären Suchbäumen beginnen.
Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
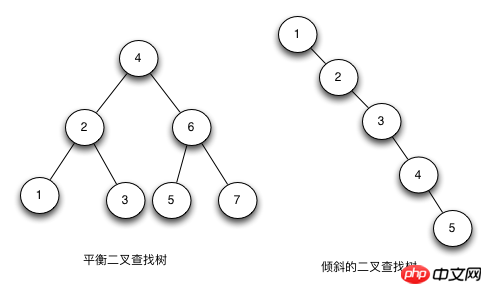
Binary Search Tree (Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)) ist ein Binärbaum. Der Wert seines linken untergeordneten Knotens ist kleiner als der Wert des übergeordneten Knotens und der Wert des rechten Knotens ist größer . Größer als der Wert des übergeordneten Knotens. Seine Höhe bestimmt seine Sucheffizienz.
Unter idealen Umständen beträgt die zeitliche Komplexität des Hinzufügens, Löschens und Änderns eines binären Suchbaums O(logN) (wobei N die Anzahl der Knoten ist) und im schlimmsten Fall O(N). . Wenn seine Höhe logN+1 beträgt, sagen wir, dass der binäre Suchbaum ausgeglichen ist.
Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)-Suchvorgang
T key = a search key
Node root = point to the root of a Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
while(true){
if(root==null){
break;
}
if(root.value.equals(key)){
return root;
}
else if(key.compareTo(root.value)<0){
root = root.left;
}
else{
root = root.right;
}
}
return null;Wie aus dem Programm ersichtlich ist, wird bei der Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)-Suche zunächst ein Vergleich mit dem aktuellen Knoten durchgeführt:
Wenn gleich, geben Sie den aktuellen Knoten zurück.
Wenn er kleiner als der aktuelle Knoten ist, suchen Sie weiter nach dem linken Knoten des aktuellen Knotens.
Wenn es größer als der aktuelle Knoten ist, suchen Sie weiter nach dem rechten Knoten des aktuellen Knotens.
Bis der aktuelle Knotenzeiger leer ist oder der entsprechende Knoten gefunden wird, endet die Programmsuche.
Einfügeoperation von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
Node node = create a new node with specify value
Node root = point the root node of a Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
Node parent = null;
//find the parent node to append the new node
while(true){
if(root==null)break;
parent = root;
if(node.value.compareTo(root.value)<=0){
root = root.left;
}else{
root = root.right;
}
}
if(parent!=null){
if(node.value.compareTo(parent.value)<=0){//append to left
parent.left = node;
}else{//append to right
parent.right = node;
}
}Die Einfügeoperation findet zunächst den übergeordneten Knoten des einzufügenden Knotens. Die Logik zum Suchen des übergeordneten Knotens ist dieselbe kleiner als die Größe links, groß rechts. Nachdem Sie den übergeordneten Knoten gefunden haben, vergleichen Sie den übergeordneten Knoten, fügen Sie den kleineren in den linken Knoten des übergeordneten Knotens und den größeren in den rechten Knoten des übergeordneten Knotens ein.
Löschvorgang von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
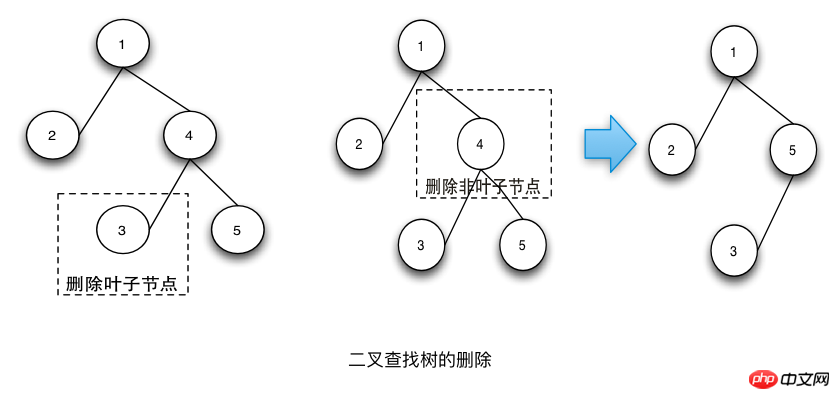
Die Schritte für den Löschvorgang sind wie folgt:
Suchen Sie den Knoten, der gelöscht werden soll.
Wenn der zu löschende Knoten ein Blattknoten ist, löschen Sie ihn direkt.
Wenn der zu löschende Knoten kein Blattknoten ist, suchen Sie zunächst den Nachfolgeknoten des zu löschenden Knotens in der richtigen Reihenfolge und ersetzen Sie ihn durch den Wert des zu löschenden Knotens mit dem Wert des Nachfolgeknotens gelöscht und dann Nachfolgeknoten löschen.
Probleme mit Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)
Das Hauptproblem bei Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild) besteht darin, dass Zahlen beim Einfügen unterschiedlich sind Die Reihenfolge führt dazu, dass die Höhe des Baums unterschiedlich ist, und die Höhe des Baums wirkt sich direkt auf die Sucheffizienz des Baums aus. Die ideale Höhe ist logN. Im schlimmsten Fall liegen alle Knoten auf einer diagonalen Linie und die Höhe eines solchen Baums beträgt N.
RBTree
Basierend auf den bestehenden Problemen von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild) wurde ein neuer Baum erstellt – Balanced Binary Search Tree (Balanced Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)). Beim Einfügen und Löschen behält der ausgeglichene Baum durch Rotationsvorgänge die Höhe bei logN bei. Zwei repräsentative ausgeglichene Bäume sind AVL-Bäume und rot-schwarze Bäume. Aufgrund der komplexen Implementierung und der schlechten Einfüge- und Löschleistung von AVL-Bäumen ist ihre Anwendung in tatsächlichen Umgebungen nicht so gut wie die von Rot-Schwarz-Bäumen.
Red-Black Tree (im Folgenden als RBTree bezeichnet) verfügt über eine Vielzahl praktischer Anwendungen, wie z. B. den vollständig fairen Scheduler im Linux-Kernel, hochpräzise Timer, ext3-Dateisysteme usw. in verschiedenen Sprachen Funktionsbibliotheken wie Javas TreeMap und TreeSet, C++ STLs Map, Multimap, Multiset usw.
RBTree ist auch eine der am häufigsten verwendeten persistenten Datenstrukturen in funktionalen Sprachen und spielt auch eine wichtige Rolle in der Computergeometrie. Erwähnenswert ist, dass die Leistung der HashMap-Implementierung in Java 8 durch das Ersetzen verknüpfter Listen durch RBTree verbessert wurde.
Definition von RBTree
Die Definition von RBTree lautet wie folgt:
Jeder Knoten hat eine Farbe, schwarz oder rot
Der Wurzelknoten ist schwarz
Zwischen dem übergeordneten und dem untergeordneten Knoten dürfen sich keine zwei aufeinanderfolgenden roten Knoten befinden
Jeder Knoten nach unten Um die Blattknoten seiner Nachkommen zu durchlaufen, muss die Anzahl der übergebenen schwarzen Knoten gleich sein
Leere Knoten werden als schwarz betrachtet
Datenstruktur Es wird wie folgt ausgedrückt:
class Node<T>{
public T value;
public Node<T> parent;
public boolean isRed;
public Node<T> left;
public Node<T> right;
}RBTree ist theoretisch immer noch ein Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)-Baum, aber es behält das Gleichgewicht des Baums beim Einfügen und Löschen von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)-Operationen bei, dh stellt sicher, dass die Höhe des Baums gewährleistet ist ist in [logN,logN+ 1] (Theoretisch kann die Höhe von RBTree im Extremfall 2 * logN erreichen, in der Praxis ist dies jedoch schwierig). Auf diese Weise bleibt die Suchzeitkomplexität von RBTree immer bei O(logN) und liegt nahe am idealen Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild). Die zeitliche Komplexität der Lösch- und Einfügevorgänge von RBTree beträgt ebenfalls O(logN). Die Suchoperation von RBTree ist die Suchoperation von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild).
Rotationsoperation von RBTree
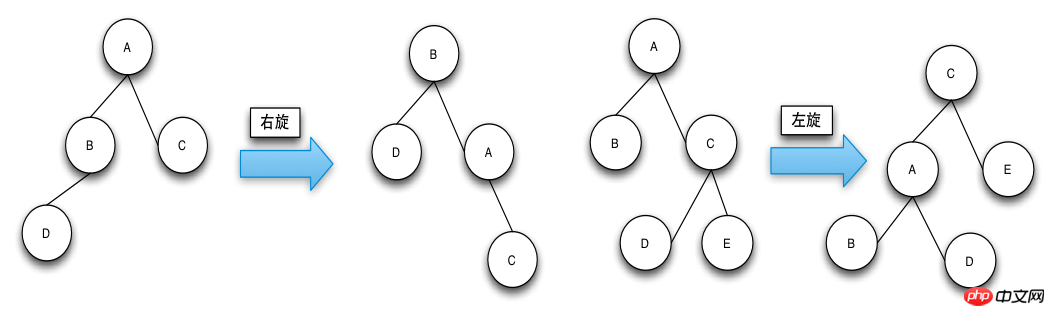
Der Zweck der Rotationsoperation (Rotieren) besteht darin, die Knotenfarbe an die Definition anzupassen und dafür zu sorgen, dass die Höhe von RBTree ein Gleichgewicht erreicht.
Drehen ist in Linksdrehung (Linksdrehung) und Rechtsdrehung (Rechtsdrehung) unterteilt. Die Methode zur Unterscheidung von Linksdrehung und Rechtsdrehung ist: Der zu drehende Knoten steigt von oben nach oben Links zum übergeordneten Knoten, was eine Rechtsdrehung bedeutet, und der zu drehende Knoten bewegt sich von rechts zum übergeordneten Knoten. Der Aufstieg zum übergeordneten Knoten ist eine Linksdrehung.
RBTree-Suchvorgang
RBTree-Suchvorgang ist derselbe wie der Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild)-Suchvorgang. Bitte beachten Sie den Suchoperationscode von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild).
Einfügevorgang von RBTree
Die Einfügemethode von RBTree ist die gleiche wie die von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild). Nach dem Einfügen ist der Baum jedoch möglicherweise unausgeglichen fix (hier als Einfügungsfix bezeichnet), sodass es der Definition von RBTree entspricht.
Der neu eingefügte Knoten ist rot. Wenn der Einfügungsreparaturvorgang auf einen übergeordneten Knoten trifft, dessen Farbe schwarz ist, wird der Reparaturvorgang beendet. Mit anderen Worten: Der Reparaturvorgang muss nur dann eingefügt werden, wenn der übergeordnete Knoten ein roter Knoten ist.
Der Einfüge- und Reparaturvorgang ist in die folgenden drei Situationen unterteilt, und die übergeordneten Knoten der neu eingefügten Knoten sind alle rot:
Der Onkelknoten ist ebenfalls rot .
Der Onkelknoten ist leer und der Großelternknoten, der übergeordnete Knoten und der neue Knoten liegen auf einer diagonalen Linie.
Der Onkelknoten ist leer und der Großelternknoten, der übergeordnete Knoten und der neue Knoten stehen nicht auf einem Schrägstrich.
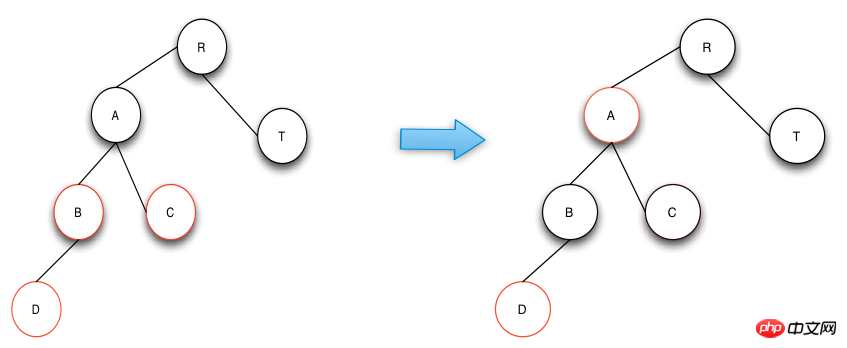
Einfügeoperation – Fall 1
Die Operation von Fall 1 besteht darin, die Farben des übergeordneten Knotens, des Onkelknotens und des Großelternknotens zu vertauschen, was der Definition von entspricht RBTree. Das heißt, ein hohes Maß an Ausgewogenheit bleibt erhalten und die Farbe nach der Reparatur entspricht auch dem dritten und vierten von RBTree definierten Punkt. In der folgenden Abbildung wird Knoten A nach Abschluss des Vorgangs zu einem neuen Knoten. Wenn der übergeordnete Knoten von Knoten A nicht schwarz ist, fahren Sie mit dem Reparaturvorgang fort.
Einfügeoperation – Fall 2
Die Operation von Fall 2 besteht darin, Knoten B nach rechts zu drehen und die Farben mit dem übergeordneten Knoten A zu vertauschen. Durch diesen Reparaturvorgang entsprechen Höhe und Farbe von RBTree der Definition eines rot-schwarzen Baums. Wenn die Knoten B und C beide rechte Knoten sind, ändern Sie einfach die Operation auf Linksdrehung.
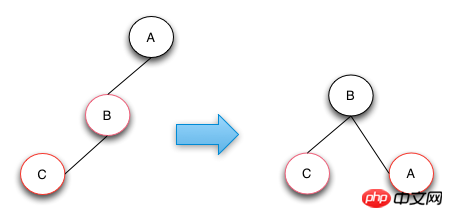
Einfügeoperation – Fall 3
Die Operation von Fall 3 besteht darin, den C-Knoten nach links zu drehen und ihn so von Fall 3 in Fall 2 umzuwandeln, und dann für Nur die Operationsverarbeitung in Fall 2 durchführen. Der Fall 2-Vorgang führt eine Rechtsdrehung und einen Farbwechsel durch, um das Ziel zu erreichen. Wenn die Struktur des Baums die Spiegelstruktur der folgenden Abbildung ist, müssen Sie nur die entsprechende Linksdrehung in Rechtsdrehung und die Rechtsdrehung in Linksdrehung ändern.
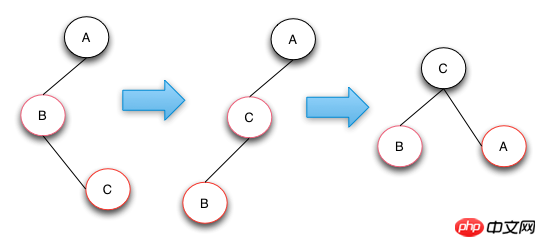
Zusammenfassung des Einfügevorgangs
Der Reparaturvorgang nach dem Einfügen ist ein Backtracking-Vorgang zum Wurzelknoten. Sobald die beteiligten Knoten den roten Anforderungen entsprechen. Black Tree Definition, der Reparaturvorgang ist abgeschlossen. Der Grund für die Rückverfolgung nach oben besteht darin, dass die Operation in Fall 1 die Farbe des übergeordneten Knotens, des Onkelknotens und des Großvaterknotens ändert, was dazu führen kann, dass der Großvaterknoten unausgeglichen ist (Rot-Schwarz-Baumdefinition 3). Zu diesem Zeitpunkt muss der Großvaterknoten als Ausgangspunkt angepasst werden (Rückwärtsverfolgung nach oben).
Wenn der Großvaterknoten nach der Anpassung immer noch auf sein Großvaterfarbproblem stößt, wird der Vorgang bis zum Wurzelknoten fortgesetzt. Per Definition ist der Wurzelknoten immer schwarz. Im Aufwärtsverfolgungsprozess werden Anpassungen für die drei eingefügten Situationen vorgenommen. Bis die Definition eines rot-schwarzen Baumes erfüllt ist. Bis alle beteiligten Knoten die Definition eines Rot-Schwarz-Baums erfüllen, endet der Reparaturvorgang.
Wenn sich die entsprechende Operation in den oben genannten drei Situationen im rechten Teilbaum befindet, führen Sie einfach die entsprechende Spiegeloperation aus.
RBTree-Löschvorgang
Das erste, was Sie für den Löschvorgang tun müssen, ist der Löschvorgang von Eingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild). Wenn es sich um einen Blattknoten handelt, wird dieser gelöscht Wird direkt gelöscht. Wenn es sich um einen Nicht-Blattknoten handelt, wird die Position des zu löschenden Knotens durch den entsprechenden Nachfolgeknoten der Durchquerung in der Reihenfolge ersetzt. Nach dem Löschen müssen Sie einen Lösch- und Reparaturvorgang durchführen, damit der Baum der Definition eines rot-schwarzen Baums entspricht und die Höhe des rot-schwarzen Baums, der der Definition entspricht, ausgeglichen wird.
Der Lösch- und Reparaturvorgang ist abgeschlossen, wenn der gelöschte Knoten ein roter Knoten ist oder den Wurzelknoten erreicht.
Der Lösch- und Reparaturvorgang dient nur zum Löschen schwarzer Knoten. Wenn die schwarzen Knoten gelöscht werden, entspricht der gesamte Baum nicht der vierten Definition von RBTree. Was getan werden muss, ist, die schwarzen Knoten von den Geschwisterknoten zu trennen. Wenn die Geschwisterknoten keine schwarzen Knoten zum Ausleihen haben, können wir nur zurückverfolgen und von der Anzahl der schwarzen Knoten auf jeder Ebene eins subtrahieren, um den gesamten Baum zu erstellen entspricht der Definition des roten Knotens.
Die Gesamtidee des Löschvorgangs besteht darin, die schwarzen Knoten von den Geschwisterknoten zu trennen, um das lokale Gleichgewicht des Baums aufrechtzuerhalten. Ob das lokale Gleichgewicht erreicht wird, hängt davon ab, ob der Gesamtbaum ausgeglichen ist . Wenn es unausgeglichen ist, wird es nachträglich angepasst.
Der Lösch- und Reparaturvorgang ist in vier Situationen unterteilt (nach dem Löschen des schwarzen Knotens):
Der Geschwisterknoten des zu löschenden Knotens ist ein roter Knoten.
Die Geschwisterknoten des zu löschenden Knotens sind schwarze Knoten, und die untergeordneten Knoten der Geschwisterknoten sind alle schwarz.
Der Geschwisterknoten des anzupassenden Knotens ist ein schwarzer Knoten, und der linke untergeordnete Knoten des Geschwisterknotens ist rot und der rechte Knoten ist schwarz (der Geschwisterknoten befindet sich auf dem rechts). Wenn der Geschwisterknoten links ist, ist der rechte untergeordnete Knoten des Geschwisterknotens rot und der linke Knoten ist schwarz.
待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
删除操作-case 1
由于兄弟节点是红色节点的时候,无法借调黑节点,所以需要将兄弟节点提升到父节点,由于兄弟节点是红色的,根据RBTree的定义,兄弟节点的子节点是黑色的,就可以从它的子节点借调了。
case 1这样转换之后就会变成后面的case 2,case 3,或者case 4进行处理了。上升操作需要对C做一个左旋操作,如果是镜像结构的树只需要做对应的右旋操作即可。
之所以要做case 1操作是因为兄弟节点是红色的,无法借到一个黑节点来填补删除的黑节点。
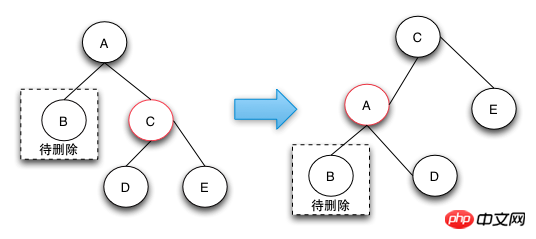
删除操作-case 2
case 2的删除操作是由于兄弟节点可以消除一个黑色节点,因为兄弟节点和兄弟节点的子节点都是黑色的,所以可以将兄弟节点变红,这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点,继续向上调整,直到整颗树的颜色符合RBTree的定义为止。
case 2这种情况下之所以要将兄弟节点变红,是因为如果把兄弟节点借调过来,会导致兄弟的结构不符合RBTree的定义,这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后,达到了局部的平衡了,但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点,接着进行修复操作。
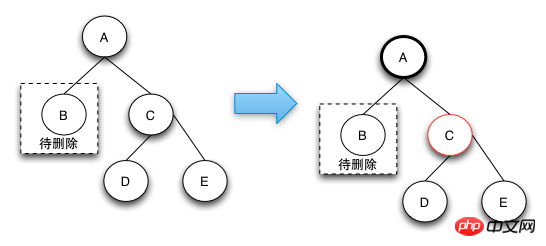
删除操作-case 3
case 3的删除操作是一个中间步骤,它的目的是将左边的红色节点借调过来,这样就可以转换成case 4状态了,在case 4状态下可以将D,E节点都阶段过来,通过将两个节点变成黑色来保证红黑树的整体平衡。
之所以说case-3是一个中间状态,是因为根据红黑树的定义来说,下图并不是平衡的,他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况,是因为可以通过借用侄子节点的红色,变成黑色来符合红黑树定义4.
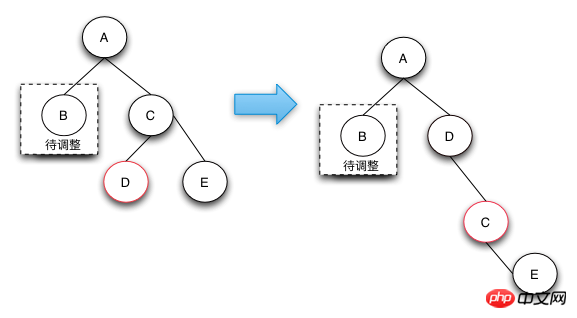
删除操作-case 4
Case 4的操作是真正的节点借调操作,通过将兄弟节点以及兄弟节点的右节点借调过来,并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的,这样的话,整棵树还是符合RBTree的定义的。
Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑,且子节点不全部为黑,才有可能借调到两个节点来做黑节点使用,从而保持整棵树都符合红黑树的定义。
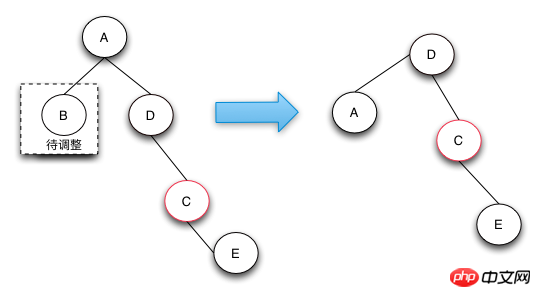
删除操作的总结
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。
RBTree的Java实现
public class RBTreeNode<T extends Comparable<T>> {
private T value;//node value
private RBTreeNode<T> left;//left child pointer
private RBTreeNode<T> right;//right child pointer
private RBTreeNode<T> parent;//parent pointer
private boolean red;//color is red or not red
public RBTreeNode(){}
public RBTreeNode(T value){this.value=value;}
public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}
public T getValue() {
return value;
}
void setValue(T value) {
this.value = value;
}
RBTreeNode<T> getLeft() {
return left;
}
void setLeft(RBTreeNode<T> left) {
this.left = left;
}
RBTreeNode<T> getRight() {
return right;
}
void setRight(RBTreeNode<T> right) {
this.right = right;
}
RBTreeNode<T> getParent() {
return parent;
}
void setParent(RBTreeNode<T> parent) {
this.parent = parent;
}
boolean isRed() {
return red;
}
boolean isBlack(){
return !red;
}
/**
* is leaf node
**/
boolean isLeaf(){
return left==null && right==null;
}
void setRed(boolean red) {
this.red = red;
}
void makeRed(){
red=true;
}
void makeBlack(){
red=false;
}
@Override
public String toString(){
return value.toString();
}
}
public class RBTree<T extends Comparable<T>> {
private final RBTreeNode<T> root;
//node number
private java.util.concurrent.atomic.AtomicLong size =
new java.util.concurrent.atomic.AtomicLong(0);
//in overwrite mode,all node's value can not has same value
//in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
private volatile boolean overrideMode=true;
public RBTree(){
this.root = new RBTreeNode<T>();
}
public RBTree(boolean overrideMode){
this();
this.overrideMode=overrideMode;
}
public boolean isOverrideMode() {
return overrideMode;
}
public void setOverrideMode(boolean overrideMode) {
this.overrideMode = overrideMode;
}
/**
* number of tree number
* @return
*/
public long getSize() {
return size.get();
}
/**
* get the root node
* @return
*/
private RBTreeNode<T> getRoot(){
return root.getLeft();
}
/**
* add value to a new node,if this value exist in this tree,
* if value exist,it will return the exist value.otherwise return null
* if override mode is true,if value exist in the tree,
* it will override the old value in the tree
*
* @param value
* @return
*/
public T addNode(T value){
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* find the value by give value(include key,key used for search,
* other field is not used,@see compare method).if this value not exist return null
* @param value
* @return
*/
public T find(T value){
RBTreeNode<T> dataRoot = getRoot();
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
dataRoot = dataRoot.getRight();
}else if(cmp>0){
dataRoot = dataRoot.getLeft();
}else{
return dataRoot.getValue();
}
}
return null;
}
/**
* remove the node by give value,if this value not exists in tree return null
* @param value include search key
* @return the value contain in the removed node
*/
public T remove(T value){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
parent = dataRoot;
dataRoot = dataRoot.getRight();
}else if(cmp>0){
parent = dataRoot;
dataRoot = dataRoot.getLeft();
}else{
if(dataRoot.getRight()!=null){
RBTreeNode<T> min = removeMin(dataRoot.getRight());
//x used for fix color balance
RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
boolean isParent = min.getRight()==null;
min.setLeft(dataRoot.getLeft());
setParent(dataRoot.getLeft(),min);
if(parent.getLeft()==dataRoot){
parent.setLeft(min);
}else{
parent.setRight(min);
}
setParent(min,parent);
boolean curMinIsBlack = min.isBlack();
//inherit dataRoot's color
min.setRed(dataRoot.isRed());
if(min!=dataRoot.getRight()){
min.setRight(dataRoot.getRight());
setParent(dataRoot.getRight(),min);
}
//remove a black node,need fix color
if(curMinIsBlack){
if(min!=dataRoot.getRight()){
fixRemove(x,isParent);
}else if(min.getRight()!=null){
fixRemove(min.getRight(),false);
}else{
fixRemove(min,true);
}
}
}else{
setParent(dataRoot.getLeft(),parent);
if(parent.getLeft()==dataRoot){
parent.setLeft(dataRoot.getLeft());
}else{
parent.setRight(dataRoot.getLeft());
}
//current node is black and tree is not empty
if(dataRoot.isBlack() && !(root.getLeft()==null)){
RBTreeNode<T> x = dataRoot.getLeft()==null
? parent :dataRoot.getLeft();
boolean isParent = dataRoot.getLeft()==null;
fixRemove(x,isParent);
}
}
setParent(dataRoot,null);
dataRoot.setLeft(null);
dataRoot.setRight(null);
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
size.decrementAndGet();
return dataRoot.getValue();
}
}
return null;
}
/**
* fix remove action
* @param node
* @param isParent
*/
private void fixRemove(RBTreeNode<T> node,boolean isParent){
RBTreeNode<T> cur = isParent ? null : node;
boolean isRed = isParent ? false : node.isRed();
RBTreeNode<T> parent = isParent ? node : node.getParent();
while(!isRed && !isRoot(cur)){
RBTreeNode<T> sibling = getSibling(cur,parent);
//sibling is not null,due to before remove tree color is balance
//if cur is a left node
boolean isLeft = parent.getRight()==sibling;
if(sibling.isRed() && !isLeft){//case 1
//cur in right
parent.makeRed();
sibling.makeBlack();
rotateRight(parent);
}else if(sibling.isRed() && isLeft){
//cur in left
parent.makeRed();
sibling.makeBlack();
rotateLeft(parent);
}else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
sibling.makeRed();
cur = parent;
isRed = cur.isRed();
parent=parent.getParent();
}else if(isLeft && !isBlack(sibling.getLeft())
&& isBlack(sibling.getRight())){//case 3
sibling.makeRed();
sibling.getLeft().makeBlack();
rotateRight(sibling);
}else if(!isLeft && !isBlack(sibling.getRight())
&& isBlack(sibling.getLeft()) ){
sibling.makeRed();
sibling.getRight().makeBlack();
rotateLeft(sibling);
}else if(isLeft && !isBlack(sibling.getRight())){//case 4
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getRight().makeBlack();
rotateLeft(parent);
cur=getRoot();
}else if(!isLeft && !isBlack(sibling.getLeft())){
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getLeft().makeBlack();
rotateRight(parent);
cur=getRoot();
}
}
if(isRed){
cur.makeBlack();
}
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
}
//get sibling node
private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
parent = node==null ? parent : node.getParent();
if(node==null){
return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
}
if(node==parent.getLeft()){
return parent.getRight();
}else{
return parent.getLeft();
}
}
private boolean isBlack(RBTreeNode<T> node){
return node==null || node.isBlack();
}
private boolean isRoot(RBTreeNode<T> node){
return root.getLeft() == node && node.getParent()==null;
}
/**
* find the successor node
* @param node current node's right node
* @return
*/
private RBTreeNode<T> removeMin(RBTreeNode<T> node){
//find the min node
RBTreeNode<T> parent = node;
while(node!=null && node.getLeft()!=null){
parent = node;
node = node.getLeft();
}
//remove min node
if(parent==node){
return node;
}
parent.setLeft(node.getRight());
setParent(node.getRight(),parent);
//don't remove right pointer,it is used for fixed color balance
//node.setRight(null);
return node;
}
private T addNode(RBTreeNode<T> node){
node.setLeft(null);
node.setRight(null);
node.setRed(true);
setParent(node,null);
if(root.getLeft()==null){
root.setLeft(node);
//root node is black
node.setRed(false);
size.incrementAndGet();
}else{
RBTreeNode<T> x = findParentNode(node);
int cmp = x.getValue().compareTo(node.getValue());
if(this.overrideMode && cmp==0){
T v = x.getValue();
x.setValue(node.getValue());
return v;
}else if(cmp==0){
//value exists,ignore this node
return x.getValue();
}
setParent(node,x);
if(cmp>0){
x.setLeft(node);
}else{
x.setRight(node);
}
fixInsert(node);
size.incrementAndGet();
}
return null;
}
/**
* find the parent node to hold node x,if parent value equals x.value return parent.
* @param x
* @return
*/
private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> child = dataRoot;
while(child!=null){
int cmp = child.getValue().compareTo(x.getValue());
if(cmp==0){
return child;
}
if(cmp>0){
dataRoot = child;
child = child.getLeft();
}else if(cmp<0){
dataRoot = child;
child = child.getRight();
}
}
return dataRoot;
}
/**
* red black tree insert fix.
* @param x
*/
private void fixInsert(RBTreeNode<T> x){
RBTreeNode<T> parent = x.getParent();
while(parent!=null && parent.isRed()){
RBTreeNode<T> uncle = getUncle(x);
if(uncle==null){//need to rotate
RBTreeNode<T> ancestor = parent.getParent();
//ancestor is not null due to before before add,tree color is balance
if(parent == ancestor.getLeft()){
boolean isRight = x == parent.getRight();
if(isRight){
rotateLeft(parent);
}
rotateRight(ancestor);
if(isRight){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}else{
boolean isLeft = x == parent.getLeft();
if(isLeft){
rotateRight(parent);
}
rotateLeft(ancestor);
if(isLeft){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}
}else{//uncle is red
parent.setRed(false);
uncle.setRed(false);
parent.getParent().setRed(true);
x=parent.getParent();
parent = x.getParent();
}
}
getRoot().makeBlack();
getRoot().setParent(null);
}
/**
* get uncle node
* @param node
* @return
*/
private RBTreeNode<T> getUncle(RBTreeNode<T> node){
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> ancestor = parent.getParent();
if(ancestor==null){
return null;
}
if(parent == ancestor.getLeft()){
return ancestor.getRight();
}else{
return ancestor.getLeft();
}
}
private void rotateLeft(RBTreeNode<T> node){
RBTreeNode<T> right = node.getRight();
if(right==null){
throw new java.lang.IllegalStateException("right node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setRight(right.getLeft());
setParent(right.getLeft(),node);
right.setLeft(node);
setParent(node,right);
if(parent==null){//node pointer to root
//right raise to root node
root.setLeft(right);
setParent(right,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(right);
}else{
parent.setRight(right);
}
//right.setParent(parent);
setParent(right,parent);
}
}
private void rotateRight(RBTreeNode<T> node){
RBTreeNode<T> left = node.getLeft();
if(left==null){
throw new java.lang.IllegalStateException("left node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setLeft(left.getRight());
setParent(left.getRight(),node);
left.setRight(node);
setParent(node,left);
if(parent==null){
root.setLeft(left);
setParent(left,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(left);
}else{
parent.setRight(left);
}
setParent(left,parent);
}
}
private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
if(node!=null){
node.setParent(parent);
if(parent==root){
node.setParent(null);
}
}
}
/**
* debug method,it used print the given node and its children nodes,
* every layer output in one line
* @param root
*/
public void printTree(RBTreeNode<T> root){
java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
if(root==null){
return ;
}
queue.add(root);
boolean firstQueue = true;
while(!queue.isEmpty() || !queue2.isEmpty()){
java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
RBTreeNode<T> n = q.poll();
if(n!=null){
String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft()
? " LE" : " RI");
String pstr = n.getParent()==null ? "" : n.getParent().toString();
String cstr = n.isRed()?"R":"B";
cstr = n.getParent()==null ? cstr : cstr+" ";
System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
if(n.getLeft()!=null){
(firstQueue ? queue2 : queue).add(n.getLeft());
}
if(n.getRight()!=null){
(firstQueue ? queue2 : queue).add(n.getRight());
}
}else{
System.out.println();
firstQueue = !firstQueue;
}
}
}
public static void main(String[] args) {
RBTree<String> bst = new RBTree<String>();
bst.addNode("d");
bst.addNode("d");
bst.addNode("c");
bst.addNode("c");
bst.addNode("b");
bst.addNode("f");
bst.addNode("a");
bst.addNode("e");
bst.addNode("g");
bst.addNode("h");
bst.remove("c");
bst.printTree(bst.getRoot());
}
}代码调试的时候,printTree输出格式如下:
d(B) b(B d LE) g(R d RI) a(R b LE) e(B g LE) h(B g RI) f(R e RI)
括号左边表示元素的内容。括号内的第一个元素表示颜色,B表示black,R表示red;第二个元素表示父元素的值;第三个元素表示左右,LE表示在父元素的左边。RI表示在父元素的右边。
第一个元素d是root节点,由于它没有父节点,所以括号内只有一个元素。
总结
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。
Das obige ist der detaillierte Inhalt vonEingehende Analyse der Java-Implementierung von Rot-Schwarz-Bäumen (Bild). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Wann sollte @PathParam vs. @QueryParam in RESTful-APIs verwendet werden?
- Warum führt die Ganzzahldivision in Java zu unerwarteten Ergebnissen?
- Wie zeichnet man Rechtecke dauerhaft in einem JPanel: Verwenden von BufferedImages, um ein Überschreiben zu vermeiden?
- Wie kann man Unicode-Codepunkte in Java-Strings effizient durchlaufen?
- Warum wirft Java beim Zuweisen zu einer langen Variablen „Das Literal xyz des Typs int liegt außerhalb des Bereichs' aus?

