Heim >Backend-Entwicklung >Python-Tutorial >So implementieren Sie einen binären Suchbaum in Python
So implementieren Sie einen binären Suchbaum in Python
- 高洛峰Original
- 2017-03-13 15:44:531469Durchsuche
BinärSucheBaum (binärer Sortierbaum) Die Datenstruktur jedes Knotens besteht aus 1 übergeordnetem Knotenzeiger, 1 linkem untergeordnetem Zeiger, 1 untergeordnetem Zeiger und sich selbst. Der Datenteil von ist alle größer als der Knoten .
Binärer Suchbaum
Wir kennen bereits zwei verschiedene Möglichkeiten, Schlüssel-Wert-Paare in eine Sammlung zu bekommen. Erinnern Sie sich daran, wie diese Sammlungen ADT (AbstractData Type)MAP implementieren. Wir diskutieren zwei Implementierungen von ADT MAP, die listenbasierte Binärsuche und die Hash-Tabelle. In diesem Abschnitt lernen wir binäre Suchbäume kennen, bei denen es sich um eine weitere Map-Sammlung handelt, deren Schlüssel auf Werte verweisen. In diesem Fall müssen wir die tatsächliche Position des Elements im Baum nicht berücksichtigen, aber wir müssen sie kennen dass Binärbäume verwendet werden, um nach mehr Informationen zu suchen.
Suchbaumoperationen
Bevor wir uns diese Implementierung ansehen, werfen wir einen Blick auf die von ADT MAP bereitgestellte Schnittstelle. Wir werden feststellen, dass diese Schnittstelle dem Python-Wörterbuch sehr ähnlich ist.
Map() erstellt eine neue leere Kartensammlung.
put(key,val) fügt der Karte ein neues Schlüssel-Wert-Paar hinzu. Wenn der Schlüssel bereits in der Map vorhanden ist, wird der neue Wert verwendet, um den alten Wert zu ersetzen.
get(key) Stellt einen Schlüssel bereit, gibt die in der Karte gespeicherten Daten zurück oder gibt None zurück.
del Verwenden Sie die del-map[key]-Anweisung, um das Schlüssel-Wert-Paar aus der Map zu löschen.
len() gibt die Anzahl der in der Map gespeicherten Schlüssel-Wert-Paare zurück
in Wenn sich der angegebene Schlüssel in der Map befindet, verwenden Sie Geben Sie die Kartenanweisung ein. Sie gibt „True“ zurück.
Suchbaumimplementierung
Ein binärer Suchbaum, wenn die Schlüsselwerte im linken Teilbaum kleiner sind als im übergeordneten Knoten, Die Schlüsselwerte im rechten Teilbaum sind größer als das -Attribut des übergeordneten Knotens. Wir nennen diesen Baum einen BST-Suchbaum. Wie bereits erwähnt, wird uns die BST-Methode bei der Implementierung von Map dabei helfen, dies zu erreichen. Abbildung 1 veranschaulicht diese Eigenschaft eines binären Suchbaums und zeigt Schlüssel an, denen keine Werte zugeordnet sind. Beachten Sie, dass diese Eigenschaft für jeden übergeordneten und untergeordneten Knoten gilt. Alle Schlüssel im linken Teilbaum sind kleiner als der Schlüssel im Wurzelknoten und alle Schlüssel im rechten Teilbaum sind größer als der Schlüssel im Wurzelknoten.
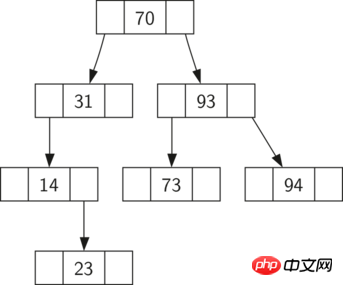
Abbildung 1: Ein einfacher binärer Suchbaum
Da Sie nun wissen, was ein binärer Suchbaum ist, schauen wir uns an, wie man einen binären Suchbaum erstellt Suchbaum: Wir fügen diese Schlüsselwerte in der Reihenfolge der in Abbildung 1 gezeigten Knoten in den Suchbaum ein. Die Knoten im Suchbaum in Abbildung 1 sind: 70, 31, 93, 94, 14, 23, 73. Da 70 der erste in den Baum eingefügte Wert ist, handelt es sich um den Wurzelknoten. Als nächstes ist 31 kleiner als 70 und daher der linke Teilbaum von 70. Als nächstes ist 93 größer als 70 und daher der rechte Teilbaum von 70. Wir haben nun zwei Ebenen des Baums gefüllt, sodass der nächste Schlüsselwert entweder der linke oder rechte Teilbaum von 31 oder 93 sein wird. Da 94 größer als 70 und 93 ist, wird es zum rechten Teilbaum von 93. Ebenso ist 14 kleiner als 70 und 31, sodass es zum linken Teilbaum von 31 wird. 23 ist ebenfalls kleiner als 31, daher muss es der linke Teilbaum von 31 sein. Allerdings ist er größer als 14, also der rechte Teilbaum von 14.
Um einen binären Suchbaum zu implementieren, verwenden wir Knoten und Verweise auf , ähnlich wie wir verknüpfte Listen und Ausdrucksbäume implementieren. Da wir in der Lage sein müssen, einen leeren binären Suchbaum zu erstellen und zu verwenden, werden wir dies mit zwei Klassen tun: Die erste Klasse nennen wir BinarySearchTree und die zweite Klasse nennen wir TreeNode. Die BinarySearchTree-Klasse hat einen Verweis auf die TreeNode-Klasse als Wurzel des binären Suchbaums. In den meisten Fällen definiert die externe Klasse die externe Methode von , die einfach prüft, ob der Baum leer ist und ob eine vorhanden ist Knoten im Baum, die Anforderung Die BinarySearchTree-Klasse enthält private Methoden, die den Stamm als Parameter definieren. Wenn in diesem Fall der Baum leer ist oder wir die Wurzel des Baums löschen möchten, müssen wir spezielle Operationen verwenden. Der Code des -Konstruktors und einiger anderer Funktionen der BinarySearchTree-Klasse ist in Listing 1 dargestellt.
Auflistung 1
class BinarySearchTree:
def init(self):
self.root = None
self.size = 0
def length(self):
return self.size
def len(self):
return self.size
def iter(self):
return self.root.iter()Die TreeNode-Klasse stellt viele Hilfsfunktionen bereit, um die Implementierung der Methoden der BinarySearchTree-Klasse zu erleichtern. Wie in Listing 2 dargestellt, wird die Struktur eines Baumknotens durch diese Hilfsfunktionen implementiert. Wie Sie sehen, können diese Hilfsfunktionen einen Knoten basierend auf seiner Position und dem Typ dieses untergeordneten Knotens als linkes oder rechtes untergeordnetes Element unterteilen. Die TreeNode-Klasse verfolgt die Eigenschaften jedes übergeordneten Knotens sehr deutlich. Warum dies wichtig ist, werden Sie sehen, wenn wir die Implementierung des Löschvorgangs besprechen.
Eine weitere interessante Sache an der TreeNode-Implementierung in Listing 2 ist, dass wir die optionalen Parameter von Python verwenden. Die optionalen Parameter erleichtern das Erstellen eines Baumknotens in verschiedenen Situationen. Manchmal möchten wir einen neuen Baumknoten erstellen, auch wenn wir bereits einen übergeordneten und untergeordneten Knoten haben. Wie die vorhandenen übergeordneten und untergeordneten Knoten können wir die übergeordneten und untergeordneten Knoten als Parameter übergeben. Manchmal erstellen wir auch einen Baum mit Schlüssel-Wert-Paaren und übergeben keine Parameter für übergeordnete oder untergeordnete Knoten. In diesem Fall verwenden wir die Standardwerte der optionalen Parameter.
Listing 2
class TreeNode:
def init(self,key,val,left=None,right=None,
parent=None):
self.key = key
self.payload = val
self.leftChild = left
self.rightChild = right
self.parent = parent
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def hasBothChildren(self):
return self.rightChild and self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = selfDa wir nun die Klassen BinarySearchTree und TreeNode haben, ist es an der Zeit, eine Put-Methode zu schreiben, mit der wir eine Binärdatei erstellen können Suchbaum. Die Put-Methode ist eine Methode der BinarySearchTree-Klasse. Diese Methode prüft, ob der Baum bereits verwurzelt ist. Wenn nicht, erstellen wir einen neuen Baumknoten und legen ihn als Wurzel des Baums fest. Wenn bereits ein Wurzelknoten vorhanden ist, rufen wir ihn selbst auf, führen eine Rekursion durch und verwenden die Hilfsfunktion _put, um den Baum gemäß dem folgenden Algorithmus zu durchsuchen:
Beginnen Sie mit dem Wurzelknoten von Durchsuchen Sie den Baum und durchsuchen Sie den Binärbaum. Um den neuen Schlüsselwert mit dem Schlüsselwert des aktuellen Knotens zu vergleichen, durchsuchen Sie den linken Teilbaum, wenn der neue Schlüsselwert kleiner als der aktuelle Knoten ist. Wenn der neue Schlüssel größer als der aktuelle Knoten ist, wird der rechte Teilbaum durchsucht.
Wenn der linke (oder rechte) Teilbaum nicht durchsucht werden kann, ist unsere Position im Baum die Stelle, an der der neue Knoten festgelegt wird.
Um einen Knoten zum Baum hinzuzufügen, erstellen Sie ein neues TreeNode-Objekt und fügen Sie dieses Objekt in den Knoten unmittelbar vor diesem Punkt ein.
Listing 3 zeigt den Python-Code zum Einfügen eines neuen Knotens in den Baum. Die Funktion _put sollte die oben genannten Schritte befolgen, um einen rekursiven Algorithmus zu schreiben. Beachten Sie, dass beim Einfügen eines neuen Unterbaums der aktuelle Knoten (AktuellerKnoten) als übergeordneter Knoten an den neuen Baum übergeben wird.
Ein wichtiges Problem beim Einfügen besteht darin, dass doppelte Schlüsselwerte nicht korrekt verarbeitet werden können. Unser Baum implementiert die Schlüsselwertreplikation, wodurch im rechten Teilbaum ein neuer Knoten mit demselben Schlüsselwert wie das Original erstellt wird Knoten. Knoten. Dies hat zur Folge, dass neue Knoten bei der Suche nicht entdeckt werden. Wir verwenden eine bessere Methode zum Umgang mit dem Einfügen doppelter Schlüsselwerte, bei der der alte Wert durch den mit dem neuen Schlüssel verknüpften Wert ersetzt wird. Die Behebung dieses Fehlers überlassen wir Ihnen als Übung.
Listing 3
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root = TreeNode(key,val)
self.size = self.size + 1
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)Mit der Implementierung der Put-Methode können wir problemlos die setitem-Methode übergeben Überladen Sie [] als Operator, um die Put-Methode aufzurufen (siehe Listing 4). Dadurch können wir Python-Anweisungen wie myZipTree['Plymouth'] = 55446 schreiben, die wie ein Python-Wörterbuch aussehen.
Listing 4
def setitem(self,k,v): self.put(k,v)
Abbildung 2 zeigt den Prozess des Einfügens eines neuen Knotens in einen binären Suchbaum. Die grauen Knoten zeigen die Reihenfolge der Baumknoten, die während des Einfügevorgangs durchlaufen werden.
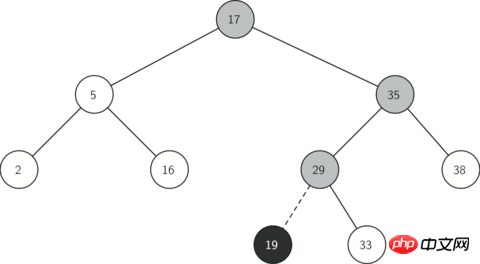
Abbildung 2: Einfügen eines Knotens mit Schlüsselwert = 19
Sobald der Baum erstellt ist, besteht die nächste Aufgabe darin, ihn für einen bestimmten Schlüsselwert zu implementieren Abrufen. Die get-Methode ist einfacher als die put-Methode, da sie den Baum einfach rekursiv durchsucht, bis entweder ein nicht übereinstimmender Blattknoten oder ein passender Schlüsselwert gefunden wird. Wenn ein passender Schlüsselwert gefunden wird, wird der Wert im Knoten zurückgegeben.
Listing 5 zeigt den Code für get, _get und getitem. Der mit der _get-Methode durchsuchte Code verfügt über dieselbe Logik zur Auswahl des linken oder rechten Teilbaums wie die put-Methode. Bitte beachten Sie, dass die _get-Methode den Wert von get in TreeNode zurückgibt. _get kann als flexible und effektive Möglichkeit verwendet werden, Parameter für andere Methoden von BinarySearchTree bereitzustellen, die möglicherweise Daten in TreeNode verwenden müssen.
Durch die Implementierung der getitem-Methode können wir eine Python-Anweisung schreiben, die aussieht, als würden wir auf ein Wörterbuch zugreifen, obwohl wir in Wirklichkeit nur einen binären Suchbaum bearbeiten, wie z. B. Z = myziptree['fargo'] . Wie Sie sehen können, ruft die getitem-Methode get auf.
Auflistung 5
def get(self,key):
if self.root:
res = self._get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key == key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def getitem(self,key):
return self.get(key)使用get,我们可以通过写一个BinarySearchTree的contains方法来实现操作,contains方法简单地调用了get方法,如果它有返回值就返回True,如果它是None就返回False。如Listing 6 所示。
Listing 6
def contains(self,key):
if self._get(key,self.root):
return True
else:
return False回顾一下contains重载的操作符,这允许我们写这样的语句:
if 'Northfield' in myZipTree:
print("oom ya ya")Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen binären Suchbaum in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

