Python implementiert den rekursiven Algorithmus „Tower of Hanoi“.

Als ich Rekursion lernte, gab es eine Übung namens „Turm von Hanoi“. Der Turm von Hanoi sollte ein klassischer Einführungsfall für das Erlernen rekursiver Computeralgorithmen sein, also dachte ich, ich könnte einen Blog schreiben, um meine Meinung zu äußern. Ich weiß noch nicht, wie man diesen Markdown-Editor verwendet, und das Format ist möglicherweise etwas hässlich.

Ich habe im Internet ein Bild vom Turm von Hanoi gefunden Der Turm von Hanoi wurde verwendet. Verwenden Sie die mittlere Säule, um die Scheiben auf der Säule ganz links von groß nach klein zu stapeln. Um es ganz klar auszudrücken: c sollte das gleiche sein wie das Original a

Hör auf, Unsinn zu reden, zeigen wir zuerst den Code

def move(n, a, buffer, c):
  if(n == 1):
    print(a,"->",c)
    return
  move(n-1, a, c, buffer)
  move(1, a, buffer, c)
  move(n-1, buffer, a, c)
move(3, "a", "b", "c")

Zuerst wird eine Bewegungsfunktion definiert, wobei vier Parameter die darstellen Das Nummernschild an der A-Säule heißt zum besseren Verständnis Puffer. Dann ist c die Zielspalte Funktionscode
Die allgemeine Schreibweise der Rekursion muss eine Bedingung zum Beenden der Rekursionsschleife sein. Wenn also festgestellt wird, dass die Anzahl der Platten in Spalte a 1 ist, kann die Rekursion beendet und zurückgegeben werden, wenn nur eine vorhanden ist Platte auf Spalte a, a muss nach c verschoben werden. Der Fokus liegt auf dem folgenden Code. Rekursion ist eigentlich ein sehr abstrakter Algorithmus, um über das Problem des Turms von Hanoi nachzudenken Säule als zwei Teile, die obere Platte und die untere Platte

Es ist uns egal, wie viele Platten sich oben befinden Der Vorgang besteht jedes Mal darin, die Bodenplatte durch den Puffer von Spalte b zu Spalte c zu bewegen.

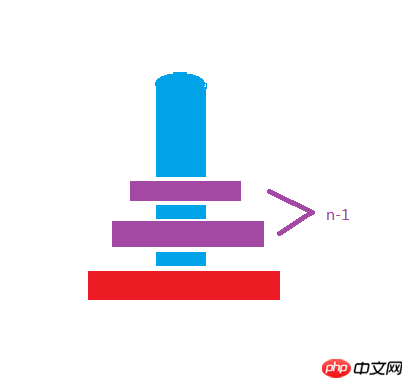
Kinder müssen darüber nachdenken, warum Jiang Zi sich bewegt. Wenn Sie das Spiel „Tower of Hanoi“ selbst spielen, werden Sie feststellen, dass dieses Spiel ständig über alle oben genannten Möglichkeiten nachdenken muss . Verschieben Sie die Einsen auf b nach b, dann verschieben Sie die letzte und größte auf a nach c und zerbrechen Sie sich dann den Kopf, um die Einsen auf b nach c zu verschieben b muss auch zuerst das leere Element durchlaufen, d. h. a, um die n-1 Elemente über dem aktuellen b zu speichern, und dann das größte und letzte Element von b nach c verschieben auch abstrahiert werden, und der Programmalgorithmus kann auf dieser Grundlage entworfen werden

Lassen Sie uns jetzt das abstrakte Denken verwenden, um den verbleibenden Code zu interpretieren

move(n-1 , a, c, Puffer)

Dieser Code ist Dies bedeutet, dass die n-1 Elemente über der gerade erwähnten a-Spalte zuerst über c gemäß den Regeln von klein nach groß in den Puffer verschoben werden . Diese Funktion geht in die Rekursion.

move(1, a, buffer, c)

Wenn die obige Anweisung ausgeführt wird, dh nachdem die rekursive Bewegung von n-1 Platten abgeschlossen ist, Führen Sie dies aus Die Anweisung besteht darin, eine Platte in Spalte a nach c zu verschieben, die sogenannte untere Platte

move(n-1, buffer, a, c)

Der letzte Schritt besteht darin, alle n-1 Elemente auf a in den Puffer zu verschieben. Sie müssen a nach c verschieben, um die Bewegung des gesamten Turms von Hanoi abzuschließen, daher besteht der letzte Schritt natürlich darin, n-1 zu verschieben Elemente gerade jetzt. Wenn der Puffer durch a in die c-Spalte verschoben wird

Lassen Sie mich den gesamten Verschiebungsprozess aufschreiben, wobei ich 3 in der a-Spalte als Beispiel nehme

/**
我把3个盘子的汉诺塔全部通过代码演示，按缩进原则，每一个缩进即进一个递归函数，每打印一次即中止当前递归,也就是每个print
说明:
  1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果，这里就不写判断了，相信童鞋们也能看懂，也就是n不等与1时就减1进入递归
  2.请注意a,b,c柱每次进入函数的顺序，不要被形参带错路了，看准每次函数参数的实参 
**/
move(3, "a", "b", "c")
n=3:
  //开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
  move(2, "a","c","b")
  n=2:
  //开始进行n=2的一个递归，把当前a('a')柱上的n-1个盘子通过c('b'）移动到b('c')
    move(1, "a", "b", "c")
    n=1:
    //n=2的第一个递归完成,打印结果，执行当前子函数剩余代码
      print("a", "->", "c") 
    move(1, "a", "c", "b")
    n=1:
      print("a", "->", "b")
    move(1, "c", "a", "b")
    n=1:
      print("c", "->", "b")
  　  //到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
  print("a", "->", "c")
  //到这里完成移动a柱上的最后一个盘子到c柱上 
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
  move(1, "b", "c", "a")
  n=1:
  //n=2 的第二个递归完成，打印结果并执行当前子函数的剩余代码
    print("b", "->", "a")
  move(1, "b", "a", "c")
  n=1:
    print("b", "->", "c")
  move(1, "a", "b", "c")
  n=1:
    print("a", "->", "c")
    //到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成

Das endgültige Druckergebnis ist:

Nachdem die Kinder das Prinzip des rekursiven Algorithmus des Turms von Hanoi verstanden haben, werden Sie Ich kann ein Programm schreiben, um es auszuprobieren. Daher kann ich Python verwenden, um das Prinzip der Rekursion zu verstehen Rekursion in der Programmierung ist selbstverständlich!

Weitere Artikel zur Python-Implementierung des rekursiven Algorithmus „Tower of Hanoi“ finden Sie auf der chinesischen PHP-Website!