Ausführliche Erläuterung des InnoDB-Indexprinzips von MySQL

Zusammenfassung:

Dieser Artikel stellt das Wissen im Zusammenhang mit dem InnoDB-Index von MySQL vor, von verschiedenen Bäumen über Indexprinzipien bis hin zu Speicherdetails.

InnoDB ist die Standardspeicher-Engine von MySQL (vor Mysql5.5.5 war es MyISAM, Dokument). Zum Zwecke eines effizienten Lernens wird in diesem Artikel hauptsächlich InnoDB vorgestellt und zum Vergleich eine kleine Menge MyISAM verwendet.

Der Inhalt dieses Artikels stammt hauptsächlich aus Büchern und Blogs (ich werde dabei auf einige Ungenauigkeiten in der Beschreibung hinweisen).

1 Verschiedene Baumstrukturen

Ursprünglich hatte ich nicht vor, mit dem binären Suchbaum zu beginnen, da es im Internet bereits zu viele verwandte Artikel gibt, aber wenn man bedenkt, dass klare Illustrationen sehr hilfreich sind Verständnis des Problems Um zu helfen und die Vollständigkeit des Artikels sicherzustellen, wurde dieser Teil schließlich hinzugefügt.

Schauen wir uns zunächst mehrere Baumstrukturen an:

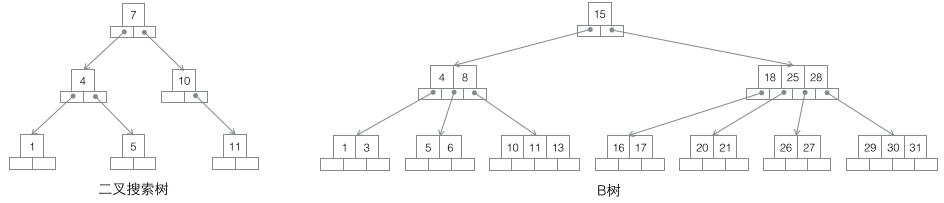
1 Binärbaum durchsuchen: Jeder Knoten hat zwei untergeordnete Knoten. Die Zunahme der Datenmenge führt offensichtlich zu einer schnellen Zunahme Dies ist nicht als Infrastruktur für die Massenspeicherung von Daten geeignet.

2 B-Baum: Ein B-Baum m-Ordnung ist ein ausgeglichener m-Wege-Suchbaum. Die wichtigste Eigenschaft besteht darin, dass die Anzahl der Schlüsselwörter j in jedem Nicht-Wurzelknoten Folgendes erfüllt: ┌m/2┐ - 1 <= j <= m - 1; die Anzahl der untergeordneten Knoten eines Knotens ist größer als die Anzahl der Schlüsselwörter um 1, sodass das Schlüsselwort zur Teilungsmarkierung des untergeordneten Knotens wird. Im Allgemeinen werden die Schlüsselwörter in der Mitte der untergeordneten Knoten im Diagramm gezeichnet, was sehr anschaulich ist und sich leicht vom B+-Baum dahinter unterscheiden lässt. Da die Daten sowohl in Blattknoten als auch in Nicht-Blattknoten vorhanden sind, ist es nicht möglich, die Schlüsselwörter im B-Baum einfach der Reihe nach zu durchlaufen, und es muss die Durchlaufmethode in der Reihenfolge verwendet werden.

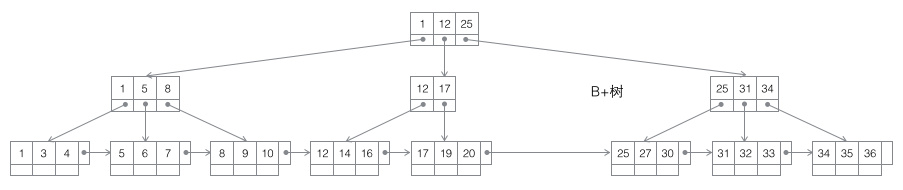
3 B+-Baum: Ein B-Baum m-Ordnung ist ein ausgeglichener m-Weg-Suchbaum. Die wichtigste Eigenschaft ist, dass die Anzahl der Schlüsselwörter j in jedem Nicht-Wurzelknoten Folgendes erfüllt: ┌m/2┐ - 1 <= j <= m; die Anzahl der Teilbäume kann höchstens so groß sein wie die Schlüsselwörter. Nicht-Blattknoten speichern das kleinste Schlüsselwort im Teilbaum. Gleichzeitig existieren Datenknoten nur in Blattknoten, und zwischen Blattknoten werden horizontale Zeiger hinzugefügt, was das sequentielle Durchlaufen aller Daten sehr einfach macht.

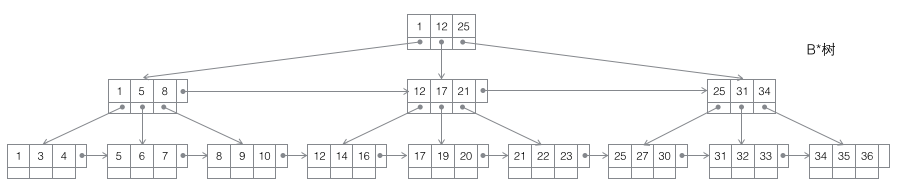
4 B*-Baum: Ein B-Baum m-Ordnung ist ein ausgeglichener m-Weg-Suchbaum. Die beiden wichtigsten Eigenschaften sind 1. Die Anzahl der in jedem Nicht-Wurzelknoten enthaltenen Schlüsselwörter j erfüllt: ┌m2/3┐ - 1 <= j <= m; Zwischen Nicht-Blattknoten werden horizontale Zeiger hinzugefügt.

　B/B+/B* Drei Bäume haben ähnliche Vorgänge, wie z. B. Abrufen/Einfügen /Knoten löschen. Hier konzentrieren wir uns nur auf die Situation beim Einfügen von Knoten und analysieren ihre Einfügungsvorgänge nur, wenn der aktuelle Knoten voll ist, da diese Aktion etwas kompliziert ist und die Unterschiede zwischen mehreren Bäumen vollständig widerspiegeln kann. Im Gegensatz dazu ist das Abrufen von Knoten relativ einfach zu implementieren, während zum Löschen von Knoten nur der umgekehrte Vorgang des Einfügens abgeschlossen werden muss (in tatsächlichen Anwendungen ist das Löschen nicht der vollständige umgekehrte Vorgang des Einfügens, und oft werden nur die Daten gelöscht und der Speicherplatz reserviert spätere Nutzung).

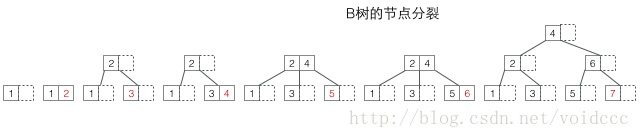
Schauen wir uns zunächst die Aufteilung des B-Baums an. Der rote Wert in der Abbildung unten ist jeweils der neu eingefügte Knoten. Immer wenn ein Knoten voll ist, muss eine Aufteilung erfolgen (die Aufteilung ist ein rekursiver Prozess, siehe Einfügung in 7 unten, der zu einer zweistufigen Aufteilung führt, da die Nicht-Blattknoten des B-Baums auch Schlüssel speichern). Werte, der vollständige Knoten nach der Aufteilung Die Werte werden an drei Stellen verteilt: 1. der ursprüngliche Knoten, 2. der übergeordnete Knoten des ursprünglichen Knotens und 3. der neue Geschwisterknoten des ursprünglichen Knotens (siehe Einfügevorgang in 5 und 7). Das Teilen kann dazu führen, dass die Höhe des Baums zunimmt (siehe Einfügevorgang unter 3 und 7), oder die Höhe des Baums bleibt davon unberührt (siehe Einfügevorgang unter 5 und 6).

Aufteilung des B+-Baums: Wenn ein Knoten voll ist, weisen Sie einen neuen Knoten zu, kopieren Sie die Hälfte der Daten im ursprünglichen Knoten auf den neuen Knoten und fügen Sie ihn schließlich hinzu der Zeiger des neuen Knotens auf den übergeordneten Knoten; die Aufteilung des B+-Baums betrifft nur den ursprünglichen Knoten und den übergeordneten Knoten, nicht jedoch die Geschwisterknoten, sodass kein Zeiger auf den Geschwisterknoten erforderlich ist.

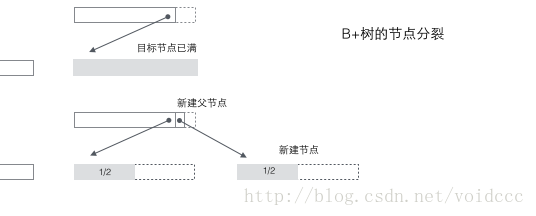
Aufteilung des B*-Baums: Wenn ein Knoten voll ist und sein nächster Geschwisterknoten nicht voll ist, verschieben Sie einen Teil der Daten auf den Geschwisterknoten, fügen Sie dann Schlüsselwörter in den ursprünglichen Knoten ein und ändern Sie schließlich den übergeordneten Knoten. Klicken Sie das Schlüsselwort des Geschwisterknotens (da sich der Schlüsselwortbereich des Geschwisterknotens geändert hat). Wenn die Brüder ebenfalls voll sind, fügen Sie einen neuen Knoten zwischen dem ursprünglichen Knoten und dem Geschwisterknoten hinzu, kopieren Sie 1/3 der Daten auf den neuen Knoten und fügen Sie schließlich den Zeiger des neuen Knotens zum übergeordneten Knoten hinzu. Es ist ersichtlich, dass die Aufteilung des B*-Baums sehr clever ist, da der B*-Baum sicherstellen muss, dass die geteilten Knoten immer noch zu 2/3 voll sind. Wenn die B+-Baum-Methode verwendet wird, reicht es aus, die vollständigen Knoten in zwei Teile zu teilen führen dazu, dass jeder Knoten nur zur Hälfte voll ist, was nicht den Anforderungen des B*-Baums entspricht. Daher besteht die vom B*-Baum verfolgte Strategie darin, weiterhin Geschwisterknoten einzufügen, nachdem der aktuelle Knoten voll ist (aus diesem Grund muss der B*-Baum eine verknüpfte Liste zwischen Brüdern an Nicht-Blattknoten hinzufügen), bis die Geschwisterknoten ebenfalls voll sind gefüllt, und ziehen Sie dann die Geschwisterknoten hoch. Zusammen tragen Sie 1/3 zum Aufbau eines neuen Knotens bei. Das Ergebnis ist, dass die drei Knoten genau zu 2/3 gefüllt sind und die Anforderungen des B*-Baums erfüllen. und alle sind glücklich.

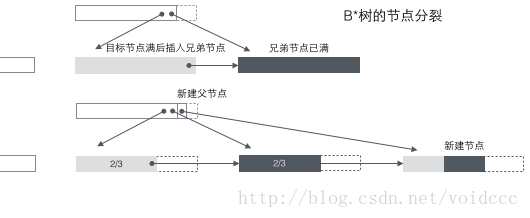
Der B+-Baum eignet sich allein aufgrund der zweischichtigen Speicherstruktur aus Computerspeicher und mechanischer Festplatte als Grundstruktur der Datenbank. Der Speicher kann einen schnellen Direktzugriff durchführen (Direktzugriff bedeutet, eine beliebige Adresse anzugeben und die Rückgabe der an dieser Adresse gespeicherten Daten anzufordern), aber die Kapazität ist gering. Der wahlfreie Zugriff auf die Festplatte erfordert mechanische Maßnahmen (1 Kopfbewegung, 2 Plattendrehungen), und die Zugriffseffizienz ist um mehrere Größenordnungen geringer als die des Speichers, aber die Festplatte hat eine größere Kapazität. Die typische Datenbankkapazität übersteigt die verfügbare Speichergröße bei weitem, was bedeutet, dass das Abrufen eines Datenelements im B+-Baum wahrscheinlich mehrere Festplatten-E/A-Vorgänge erfordert. Wie in der folgenden Abbildung dargestellt: Normalerweise kann das Auslesen eines Knotens ein Festplatten-E/A-Vorgang sein, aber Nicht-Blattknoten werden normalerweise in der Anfangsphase in den Speicher geladen, um den Zugriff zu beschleunigen. Um gleichzeitig die Geschwindigkeit der horizontalen Durchquerung zwischen Knoten zu verbessern, kann die blaue CPU-Berechnung/Speicherauslesung in der Abbildung in einen binären Suchbaum (den Seitenverzeichnismechanismus in InnoDB) in einer realen Datenbank optimiert werden.

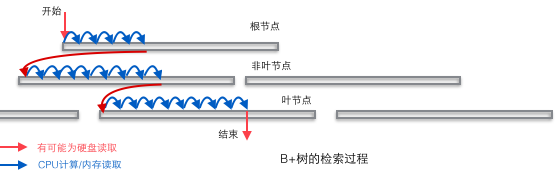
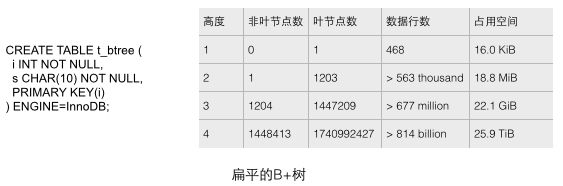
Der B+-Baum in einer echten Datenbank sollte sehr flach sein. Sie können überprüfen, wie flach der B+-Baum in InnoDB ist, indem Sie nacheinander genügend Daten in die Tabelle einfügen. Wir erstellen mit der CREATE-Anweisung wie unten gezeigt eine Testtabelle mit nur einfachen Feldern und fügen dann weitere Daten hinzu, um diese Tabelle zu füllen. Anhand der statistischen Daten in der folgenden Abbildung können mehrere intuitive Schlussfolgerungen analysiert werden (siehe Referenz 1 für die Quelle). Diese Schlussfolgerungen zeigen makroskopisch den Maßstab des B+-Baums in der Datenbank.

　1 Jeder Blattknoten speichert 468 Datenzeilen und jeder Nicht-Blattknoten speichert ungefähr 1200 Schlüsselwerte. Dies ist ein ausgewogener 1200-Wege-Suchbaum!

　2 Für einen Tisch mit einer Kapazität von 22,1 G kann nur ein B+-Baum mit einer Höhe von 3 gespeichert werden. Diese Kapazität kann wahrscheinlich die Anforderungen vieler Anwendungen erfüllen. Wenn die Höhe auf 4 erhöht wird, erhöht sich die Lagerkapazität des B+-Baums sofort auf riesige 25,9 Tonnen!

　3 Für eine Tabelle mit einer Kapazität von 22,1 G beträgt die Höhe des B+-Baums 3. Wenn Sie alle Nicht-Blattknoten in den Speicher laden möchten, sind weniger als 18,8 MB Speicher erforderlich (wie um diese Schlussfolgerung zu ziehen? Denn für einen Baum mit einer Höhe von 2 benötigen 1203 Blattknoten nur 18,8 MB, während die Höhe der 22,1 G-Sekundärtabelle 3 beträgt und es gleichzeitig 1204 Nicht-Blattknoten gibt Nehmen Sie an, dass die Größe der Blattknoten größer ist als die der Nicht-Blattknoten, da die Blätter größer sind. Der Knoten speichert Zeilendaten anstelle von Blattknoten (nur Schlüssel und eine kleine Datenmenge). Speicherplatz, um sicherzustellen, dass die erforderlichen Daten in nur einem Festplatten-E/A-Vorgang abgerufen werden können, was sehr effizient ist.

　2 MySQL-Speicher-Engine und Index

Man kann sagen, dass die Datenbank einen Index haben muss. Ohne einen Index wird der Abrufprozess zu einer sequentiellen Suche, und die zeitliche Komplexität von O(n) beträgt nahezu unerträglich. Man kann sich sehr leicht vorstellen, wie eine Tabelle, die nur aus einem einzigen Schlüssel besteht, mithilfe eines B+-Baums indiziert werden kann, solange der Schlüssel im Knoten des Baums gespeichert ist. Wenn ein Datenbankeintrag mehrere Felder enthält, kann ein B+-Baum nur den Primärschlüssel speichern. Wenn ein Nicht-Primärschlüsselfeld abgerufen wird, verliert der Primärschlüsselindex seine Funktion und wird wieder zu einer sequentiellen Suche. Zu diesem Zeitpunkt sollte ein zweiter Satz von Indizes für die zweite abzurufende Spalte erstellt werden. Dieser Index wird durch unabhängige B+-Bäume organisiert. Es gibt zwei gängige Methoden, um das Problem zu lösen, dass mehrere B+-Bäume auf denselben Satz von Tabellendaten zugreifen: Eine wird als Clustered-Index (Clustered-Index) und die andere als Nicht-Clustered-Index (Sekundärindex) bezeichnet. Obwohl diese beiden Namen als Indizes bezeichnet werden, handelt es sich nicht um einen separaten Indextyp, sondern um eine Datenspeichermethode. Bei der Clustered-Index-Speicherung werden Zeilendaten und Primärschlüssel-B+-Bäume zusammen gespeichert, und Sekundärschlüssel-B+-Bäume speichern nur Sekundärschlüssel und Primärschlüssel- und Nicht-Primärschlüssel-B+-Bäume sind fast zwei Arten von Bäumen. Für die nicht gruppierte Indexspeicherung speichert der Primärschlüssel-B+-Baum Zeiger auf die tatsächlichen Datenzeilen in Blattknoten anstelle des Primärschlüssels.

InnoDB verwendet einen Clustered-Index, um den Primärschlüssel in einem B+-Baum zu organisieren, und die Zeilendaten werden auf dem Blattknoten gespeichert. Wenn Sie die Bedingung „wobei id = 14“ verwenden, um den Primärschlüssel zu finden, befolgen Sie die folgenden Schritte Der B+-Baum-Abrufalgorithmus kann den entsprechenden Blattknoten finden und dann die Zeilendaten abrufen. Wenn Sie eine bedingte Suche in der Spalte „Name“ durchführen, sind zwei Schritte erforderlich: Der erste Schritt besteht darin, den Namen im Hilfsindex-B+-Baum abzurufen und seinen Blattknoten zu erreichen, um den entsprechenden Primärschlüssel zu erhalten. Der zweite Schritt verwendet den Primärschlüssel, um eine weitere B+-Baum-Abrufoperation für die primäre Index-B+-Baumart durchzuführen und schließlich den Blattknoten zu erreichen, um die gesamte Datenzeile zu erhalten.

MyISM verwendet einen nicht gruppierten Index. Die beiden B+-Bäume des nicht gruppierten Index sehen genau gleich aus, aber der gespeicherte Inhalt ist unterschiedlich Der Index-B+-Baum speichert den Primärschlüssel. Der Sekundärschlüssel-Index-B+-Baum speichert Sekundärschlüssel. Die Tabellendaten werden an einem separaten Ort gespeichert. Die Blattknoten der beiden B+-Bäume verwenden eine Adresse, um auf die tatsächlichen Tabellendaten zu verweisen. Es gibt keinen Unterschied zwischen den beiden Schlüsseln. Da die Indexbäume unabhängig sind, erfordert der Abruf durch Sekundärschlüssel keinen Zugriff auf den Indexbaum für den Primärschlüssel.

Um den Unterschied zwischen diesen beiden Indizes anschaulicher zu veranschaulichen, stellen wir uns eine Tabelle vor, die 4 Datenzeilen speichert, wie unten gezeigt. Dabei dient Id als primärer Index und Name als sekundärer Index. Das Diagramm zeigt deutlich den Unterschied zwischen Clustered-Index und Non-Clustered-Index.

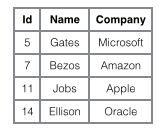
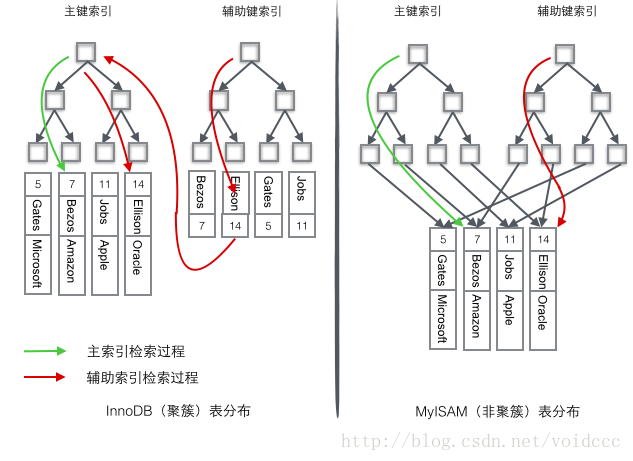
Wir konzentrieren uns auf den Clustered-Index. Es scheint, dass die Effizienz des Clustered-Index offensichtlich geringer ist als die des Nicht-Clustered-Index Index, denn jedes Mal, wenn der Hilfsindex für die Suche verwendet wird, sind zwei B+-Baumsuchen erforderlich. Was sind die Vorteile des Clustered-Index?

1 Da die Zeilendaten und Blattknoten zusammen gespeichert werden, werden der Primärschlüssel und die Zeilendaten zusammen in den Speicher geladen. Wenn der Blattknoten gefunden wird, können die Daten sofort zurückgegeben werden Organisiert nach der Primärschlüssel-ID. Erhalten Sie Daten schneller.

　2 Der Hilfsindex verwendet den Primärschlüssel als „Zeiger“ anstelle des Adresswerts als Zeiger. Der Vorteil besteht darin, dass der Wartungsaufwand des Hilfsindex beim Verschieben von Zeilen oder beim Aufteilen von Datenseiten reduziert wird Durch die Verwendung des Primärschlüsselwerts als Zeiger nimmt der Hilfsindex mehr Platz ein. Der Vorteil besteht darin, dass InnoDB beim Verschieben von Zeilen den „Zeiger“ im Hilfsindex nicht aktualisieren muss. Das heißt, die Position der Zeile (die sich in der Implementierung über die 16K-Seite befindet, die später behandelt wird) ändert sich, wenn die Daten in der Datenbank geändert werden (die vorherige Aufteilung des B+-Baumknotens und die Seitenaufteilung) und Sie können einen Clustered-Index verwenden. Es ist garantiert, dass der Hilfsindexbaum unabhängig davon, wie sich die Knoten des Primärschlüssel-B+-Baums ändern, nicht beeinträchtigt wird.

　 3-Seiten-Struktur

Wenn der vorherige Inhalt auf die Erläuterung der Prinzipien ausgerichtet ist, beginnt der spätere Inhalt, sich mit der spezifischen Umsetzung zu befassen.

Um die Implementierung von InnoDB zu verstehen, müssen wir die Seitenstruktur erwähnen. Die Seite ist die grundlegendste Komponente des gesamten InnoDB-Speichers und die kleinste Einheit der InnoDB-Datenträgerverwaltung diese Seitenstruktur. Zu den gängigen Seitentypen gehören Datenseiten (B-Tree-Knoten), Rückgängig-Seiten (Rückgängig-Protokollseiten), Systemseiten (Systemseiten), Transaktionsdatenseiten (Transaktionssystemseiten) usw. Die Größe einer einzelnen Seite beträgt 16 KB (gesteuert durch das Kompilierungsmakro UNIV_PAGE_SIZE). Jede Seite wird durch einen 32-Bit-Int-Wert eindeutig identifiziert, was der maximalen Speicherkapazität von InnoDB von 64 TB entspricht (16 KB * 2 ^ 32 = 64 TB). Die Grundstruktur einer Seite ist wie folgt:

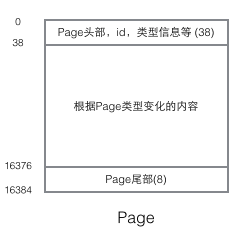
Jede Seite hat einen gemeinsamen Kopf und ein gemeinsames Ende, aber der Inhalt in der Mitte ändert sich je nach Seitentyp. Es gibt einige Daten, die uns im Header der Seite wichtig sind. Die folgende Abbildung zeigt die detaillierten Informationen des Headers der Seite:

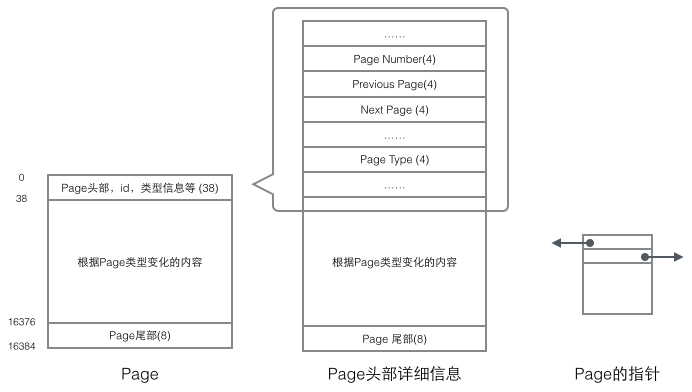
Wir konzentrieren uns auf den Datenfeldern, die sich auf die Organisationsstruktur beziehen: Der Header der Seite speichert zwei Zeiger, die jeweils auf die vorherige Seite und die nächste Seite verweisen. Der Header enthält außerdem Informationen zum Seitentyp und eine Nummer, die zur eindeutigen Identifizierung der Seite verwendet wird. Basierend auf diesen beiden Hinweisen können wir uns leicht vorstellen, dass Page in eine doppelt verknüpfte Listenstruktur eingebunden ist.

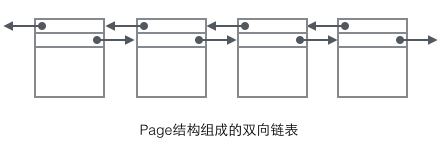
Wenn wir uns den Hauptinhalt der Seite ansehen, konzentrieren wir uns hauptsächlich auf die Speicherung von Zeilendaten und Indizes. Sie befinden sich alle im Abschnitt „Benutzerdatensätze“. Datensätze nehmen den größten Teil des Platzes der Seite ein. Benutzerdatensätze bestehen nacheinander aus Datensätzen, und jeder Datensatz stellt einen Knoten (Nicht-Blattknoten und Blattknoten) im Indexbaum dar. Innerhalb einer Seite werden Kopf und Ende einer einfach verknüpften Liste durch zwei Datensätze mit festem Inhalt dargestellt. „Infimum“ in Form einer Zeichenfolge stellt den Anfang und „Supremum“ das Ende dar. Diese beiden Datensätze, die den Anfang und das Ende darstellen, werden im Systemdatensatzsegment gespeichert. Die Systemdatensätze und Benutzerdatensätze sind zwei parallele Segmente. Es gibt 4 verschiedene Datensätze in InnoDB, nämlich 1 Nicht-Blattknoten des Primärschlüssel-Indexbaums, 2 Blattknoten des Primärschlüssel-Indexbaums, 3 Nicht-Blattknoten des Hilfsschlüssel-Indexbaums und 4 Blattknoten des Hilfsschlüssel-Indexbaums. Es gibt einige Unterschiede im Datensatzformat dieser vier Knoten, aber alle speichern Next-Zeiger, die auf den nächsten Datensatz zeigen. Wir werden diese vier Knotentypen später im Detail vorstellen. Im Moment müssen Sie sich Record nur als einfach verknüpften Listenknoten vorstellen, der Daten speichert und einen Next-Zeiger enthält.

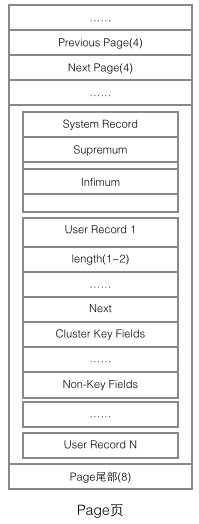
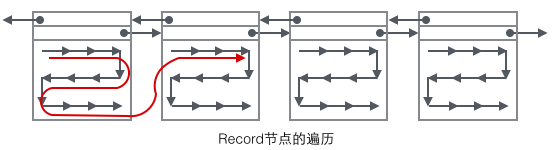
Der Benutzerdatensatz liegt in Form einer einfach verknüpften Liste auf der Seite vor. Zunächst sind die Daten in der Reihenfolge des Einfügens angeordnet, aber wenn neue Daten eingefügt werden, werden sie gelöscht Wenn Daten gelöscht werden, wird die physische Reihenfolge der Daten chaotisch, die logische Reihenfolge bleibt jedoch erhalten.

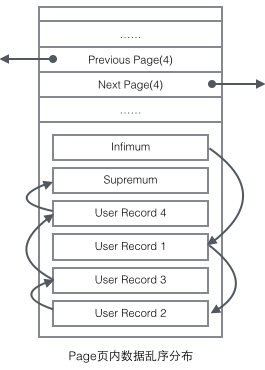
Wenn man die Organisationsform des Benutzerdatensatzes mit mehreren Seiten kombiniert, sieht man ein etwas vollständiges Formular.

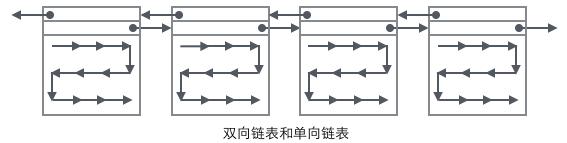
Schauen wir uns nun an, wie man einen Datensatz findet:

1. Beginnen Sie mit der Durchquerung eines indizierten B+-Baums durch den Wurzelknoten und erreichen Sie schließlich einen indizierten B+ Baum durch Nicht-Blattknoten auf jeder Seite, alle Blattknoten werden auf dieser Seite gespeichert.

　2 Durchlaufen Sie die einfach verknüpfte Liste ausgehend vom Knoten „Infimum“ auf der Seite (dieser Durchlauf wird häufig optimiert) und kehren Sie erfolgreich zurück, wenn der Schlüssel gefunden wird. Wenn der Datensatz „supremum“ erreicht, bedeutet dies, dass auf der aktuellen Seite kein geeigneter Schlüssel vorhanden ist. Zu diesem Zeitpunkt müssen Sie den Zeiger auf die nächste Seite der Seite verwenden, um zur nächsten Seite zu springen und die Suche nacheinander fortzusetzen „Infimum“.

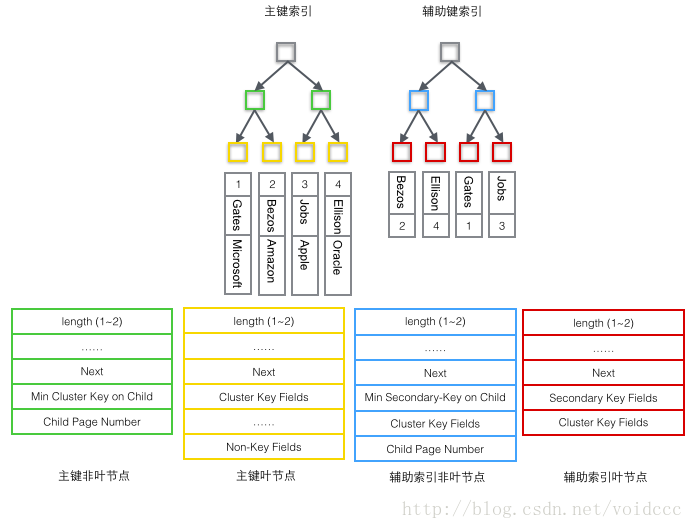
Werfen wir einen detaillierten Blick darauf, welche Daten in verschiedenen Datensatztypen gespeichert sind. Entsprechend den verschiedenen B+-Baumknoten können Benutzerdatensätze wie gezeigt in vier Formate unterteilt werden in der Abbildung unten nach Farbe unterschieden werden.

　1 Nicht-Blattknoten des Hauptindexbaums (grün)

　1 Der kleinste Wert im Primärschlüssel, der im untergeordneten Knoten gespeichert ist (Min Cluster Key on Child). ), das ist ein B+-Baum Notwendig, seine Funktion besteht darin, den spezifischen Datensatzort auf einer Seite zu lokalisieren.

　2 Die Nummer der Seite, auf der sich der kleinste Wert befindet (untergeordnete Seitennummer), wird zum Auffinden des Datensatzes verwendet.

　2 Hauptblattknoten des Indexbaums (gelb)

　1 Primärschlüssel (Cluster-Schlüsselfelder), notwendig für B+-Baum, auch Teil der Datenzeile

2 Alle Spalten außer dem Primärschlüssel (Nicht-Schlüsselfelder), der die Menge aller anderen Spalten der Datenzeile außer dem Primärschlüssel ist.

Die beiden Teile 1 und 2 ergeben hier zusammen eine vollständige Datenzeile.

　3 Nicht-Blattknoten des Hilfsindexbaums nicht (blau)

　1 Der Mindestwert unter den im untergeordneten Knoten gespeicherten Hilfsschlüsselwerten (Min Secondary- Key on Child), der für den B+-Baum erforderlich ist. Seine Funktion besteht darin, die spezifische Datensatzposition in einer Seite zu lokalisieren.

　2 Primärschlüsselwert (Cluster-Schlüsselfelder), warum speichern Nicht-Blattknoten Primärschlüssel? Da der Hilfsindex nicht eindeutig sein kann, der B + -Baum jedoch erfordert, dass der Schlüsselwert eindeutig sein muss, werden hier der Wert des Hilfsschlüssels und der Wert des Primärschlüssels als tatsächlicher Schlüsselwert im B + -Baum kombiniert. Einzigartigkeit zu gewährleisten. Dies führt aber auch dazu, dass die Nicht-Blattknoten im Hilfsindex-B+-Baum 4 Byte mehr sind als die Blattknoten. (Das heißt, der blaue Knoten im Bild unten ist 4 Bytes größer als der rote Knoten)

　3 Die Nummer der Seite, auf der sich der kleinste Wert befindet (untergeordnete Seitennummer), wird zum Auffinden des Datensatzes verwendet.

　4 Blattknoten des Hilfsindexbaums (rot)

　1 Hilfsindexschlüsselwert (Sekundärschlüsselfelder), der für den B+-Baum erforderlich ist.

　2 Primärschlüsselwert (Cluster-Schlüsselfelder), der für eine weitere B+-Baumsuche im Hauptindexbaum verwendet wird, um den gesamten Datensatz zu finden.

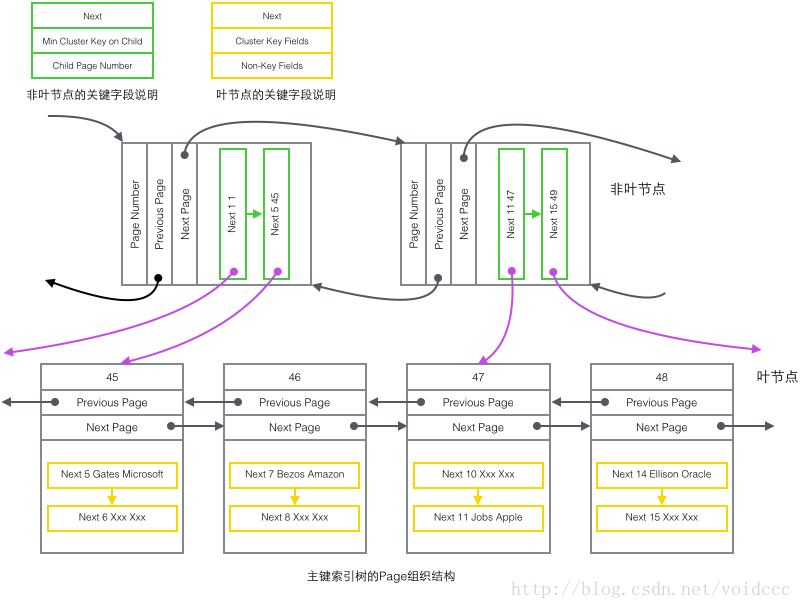
Das Folgende ist der wichtigste Teil dieses Artikels. Durch die Kombination der Struktur des B+-Baums und der Inhalte der vier zuvor vorgestellten Datensatztypen können wir endlich einen zeichnen Panoramabild. Da der B + -Baum des Hilfsindex eine ähnliche Struktur wie der Primärschlüsselindex aufweist, wird hier nur das Strukturdiagramm des Primärschlüsselindexbaums gezeichnet, der nur zwei Arten von Knoten enthält: „Primärschlüssel-Nicht-Blattknoten“ und „ Primärschlüssel-Blattknoten“, die in der Abbildung oben dargestellt sind. grüne und gelbe Teile.

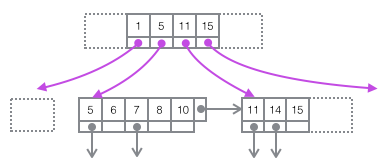
Stellen Sie das obige Bild in ein prägnanteres Baumdiagramm unten wieder her. Dies ist Teil des B+-Baums. Beachten Sie, dass es keine Eins-zu-Eins-Entsprechung zwischen der Seite und den B+-Baumknoten gibt. Die Seite wird nur als Datensatzspeichercontainer verwendet. Der Zweck ihrer Existenz besteht darin, die Stapelverwaltung des Festplattenspeichers zu erleichtern in der Baumform ist die Struktur in zwei unabhängige Knoten aufgeteilt.

Dieser Artikel fasst nur die Datenstruktur und Implementierung im Zusammenhang mit dem InnoDB-Index zusammen und bezieht sich nicht auf die tatsächliche Erfahrung mit MySQL. Dies hat hauptsächlich mehrere Gründe:

1. Das Prinzip ist der Grundstein. Nur wenn wir vollständig verstehen, wie der InnoDB-Index funktioniert, können wir ihn effizient nutzen.

　2 Prinzipielles Wissen eignet sich besonders für die Verwendung von Diagrammen. Mir persönlich gefällt diese Ausdrucksweise sehr gut.

3 In Bezug auf die InnoDB-Optimierung gibt es eine umfassendere Einführung in „High Performance MySQL“. Meine eigene Ansammlung reicht nicht aus, um diesen Inhalt zu teilen .

Noch etwas: Studenten, die mehr an der InnoDB-Implementierung interessiert sind, können sich den Blog von Jeremy Cole ansehen (Quelle für drei Referenzartikel). Dieser Mann hat an Datenbanken in Mysql, Yahoo, Twitter und Google Work gearbeitet sind großartig!

Das Obige ist eine detaillierte Erklärung des InnoDB-Indexprinzips von MySQL. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.cn)!