Heim >Java >javaLernprogramm >Java-Verbesserungskapitel (27)-----TreeMap
Java-Verbesserungskapitel (27)-----TreeMap
- 黄舟Original
- 2017-02-11 09:59:571405Durchsuche
-------------------- ------ -------------------------------------------- ------ -------------------------------------------- ------ -------------------------------------------- ------ --
Die Implementierung von TreeMap ist die Implementierung des Rot-Schwarz-Baum-Algorithmus. Um TreeMap zu verstehen, müssen Sie also über bestimmte Kenntnisse verfügen Tatsächlich lautet der Name dieses Blog-Beitrags: Analysieren Sie die Implementierung von TreeMap basierend auf dem Rot-Schwarz-Baum-Algorithmus. Um jedoch mit der Java-Verbesserungsreihe von Blog-Beiträgen übereinzustimmen, ist es besser, dies zu tun Nennen Sie es TreeMap. Durch diesen Blog-Beitrag können Sie die folgenden Wissenspunkte erhalten:
1. Das Grundkonzept der rot-schwarzen Bäume.
2. Der Implementierungsprozess des Hinzufügens von Knoten und des Löschens von Knoten im rot-schwarzen Baum.
3. Der komplexe Prozess der Linksdrehung und Rechtsdrehung roter und schwarzer Bäume.
4. Wie verwendet TreeMap in Java put und deleteEntry, um Knoten im rot-schwarzen Baum hinzuzufügen und zu löschen?
Ich denke, dass Sie durch diesen Blogbeitrag ein tieferes Verständnis von TreeMap erlangen müssen. Okay, lassen Sie uns kurz das Wissen über rot-schwarze Bäume bekannt machen.
1. Einführung in den rot-schwarzen Baum
Rot-Schwarz Der Baum wird auch als Rot-Schwarz-Binärbaum bezeichnet. Er ist in erster Linie ein Binärbaum und verkörpert alle Merkmale eines Binärbaums. Gleichzeitig ist der Rot-Schwarz-Baum ein selbstausgleichender sortierter Binärbaum.
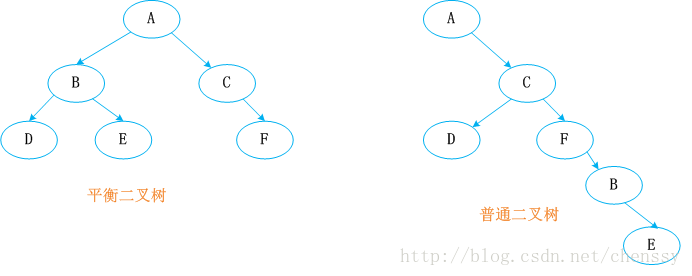
Wir wissen, dass ein einfacher Binärbaum eine grundlegende Eigenschaft erfüllen muss – das heißt, der Wert jedes Knotens im Baum ist größer als sein linker untergeordneter Knoten und kleiner als sein rechter untergeordneter Knoten Knoten. Aufgrund dieser Grundeigenschaft wird die Rückholeffizienz des Baumes erheblich verbessert. Wir wissen, dass der Prozess der Generierung eines Binärbaums sehr leicht aus dem Gleichgewicht geraten kann. Das schlimmste Szenario ist einseitig (nur rechter/linker Teilbaum). Dies führt zwangsläufig zu einer stark verringerten Abrufeffizienz des Binärbaums (O(). n)), also um den Binärbaum ausgewogen zu halten, haben Experten verschiedene Implementierungsalgorithmen vorgeschlagen, wie zum Beispiel: AVL, SBT, Spread Tree, TREAP, Rot-Schwarz-Baum usw.
Ein ausgeglichener Binärbaum muss die folgenden Eigenschaften aufweisen: Er ist ein leerer Baum oder der absolute Wert des Höhenunterschieds zwischen seinem linken und rechten Teilbaum überschreitet nicht 1 und sowohl der linke als auch der Die rechten Teilbäume sind eins. Ein ausgeglichener Binärbaum. Das heißt, für jeden Unterknoten des Binärbaums sind die Höhen seines linken und rechten Unterbaums ähnlich.
Wie der Name schon sagt, ist ein rot-schwarzer Baum ein ausgeglichener Binärbaum mit roten oder schwarzen Knoten. Er hält das Gleichgewicht aufrecht des Binärbaums durch Farbbeschränkungen. Für einen effektiven Rot-Schwarz-Binärbaum müssen wir die folgenden Regeln hinzufügen: 🎜>
2. Der Wurzelknoten ist schwarz
3. Jeder Blattknoten (NIL-Knoten, leerer Knoten) ist schwarz.
4. Wenn ein Knoten rot ist, dann hat er zwei Kinder Knoten sind alle schwarz. Das heißt, zwei benachbarte rote Knoten dürfen nicht auf einem Pfad erscheinen.
5. Alle Pfade von jedem Knoten zu jedem seiner Blätter enthalten beide die gleiche Anzahl schwarzer Knoten.
Diese Einschränkungen erzwingen eine Schlüsseleigenschaft rot-schwarzer Bäume: Der längstmögliche Weg von der Wurzel zum Blatt ist nicht mehr als der kürzeste Der mögliche Weg ist doppelt so lang. Das Ergebnis ist ein Baum, der ungefähr im Gleichgewicht ist. Da im schlimmsten Fall die Zeit für Vorgänge wie das Einfügen, Löschen und Nachschlagen eines Werts proportional zur Höhe des Baums sein muss, ermöglicht diese theoretische Obergrenze der Höhe, dass rot-schwarze Bäume im schlimmsten Fall effizient sind. im Gegensatz zum gewöhnlichen binären Suchbaum. Daher ist der Rot-Schwarz-Baum komplex und effizient, und seine Abrufeffizienz beträgt O(log n). Das Bild unten zeigt einen typischen rot-schwarzen Binärbaum.

Es umfasst drei Grundoperationen: Linksdrehung, Rechtsdrehung und Färben.
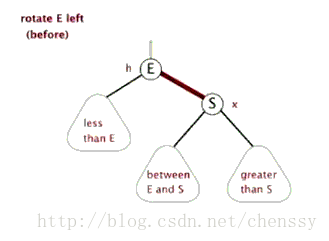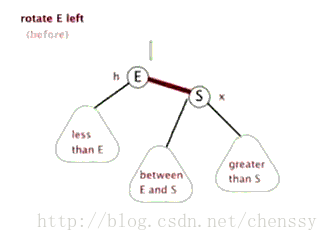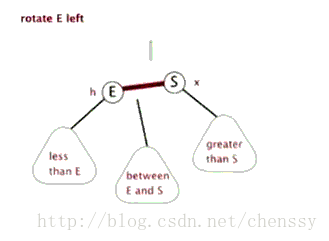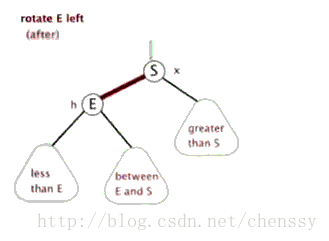
Linksdrehung
Referenzen in diesem Abschnitt:http://www.php .cn/Baidu Encyclopedia
Hinweis:Seitdem In diesem Artikel wird hauptsächlich TreeMap in Java erläutert. Es gibt keine sehr detaillierten Kenntnisse und Untersuchungen zu Rot-Schwarz-Bäumen. Wenn Sie tiefergehende Untersuchungen dazu durchführen möchten, werde ich einige gute Blog-Beiträge bereitstellen:
1, Rote und schwarze Baumserie Highlights
2,Analyse der Rot-Schwarz-Baum-Datenstruktur
3. Roter und schwarzer Baum
2. TreeMap-Datenstruktur
7ca544e9f4e9b43c0ea772e1bfa78d2a extends AbstractMapb77a8d9c3c319e50d4b02a976b347910 implements NavigableMapb77a8d9c3c319e50d4b02a976b347910, Cloneable, java.io.Serializable TreeMap enthält außerdem die folgenden wichtigen Attribute:
//比较器,因为TreeMap是有序的,通过comparator接口我们可以对TreeMap的内部排序进行精密的控制
private final Comparator99be4058f294b5c4a6207ddd3216ce19 comparator; //TreeMap红-黑节点,为TreeMap的内部类
private transient Entryb77a8d9c3c319e50d4b02a976b347910 root = null; //容器大小
private transient int size = 0; //TreeMap修改次数
private transient int modCount = 0; //红黑树的节点颜色--红色
private static final boolean RED = false; //红黑树的节点颜色--黑色
private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子
Entryb77a8d9c3c319e50d4b02a976b347910 left = null; //右孩子
Entryb77a8d9c3c319e50d4b02a976b347910 right = null; //父亲
Entryb77a8d9c3c319e50d4b02a976b347910 parent; //颜色
boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
三、TreeMap put()方法
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树增加节点
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。

对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
-
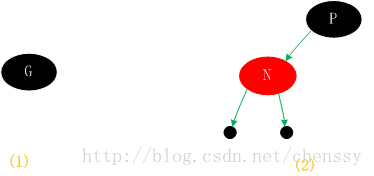
Wenn der neu eingefügte Knoten N keinen übergeordneten Knoten hat, kann er direkt als Knoten eingefügt werden. Stellen Sie die Farbe auf Schwarz ein. (Wie in Abbildung 1 (1) dargestellt)
2. Der Elternteil Knoten ist schwarz
Rot, da es gemäß Regel 4 zwei schwarze Blattknoten gibt und der Wert ist null. Da der neue Knoten N rot ist, enthält der Pfad durch seine untergeordneten Knoten gleichzeitig immer noch die gleiche Anzahl schwarzer Knoten, was auch Regel 5 erfüllt. (Wie in Abbildung 1 (2) dargestellt)

(Bild 1)
3. Wenn der übergeordnete Knoten P und der Geschwisterknoten U beide rot sind
In diesem Fall wird es bei direkter Einfügung definitiv zu einem Ungleichgewicht kommen. Wie damit umgehen? Die P- und U-Knoten werden schwarz und der G-Knoten wird rot. Da die Pfade, die durch die Knoten P und U verlaufen, zu diesem Zeitpunkt durch G verlaufen müssen, ist die Anzahl der schwarzen Knoten auf diesen Pfaden immer noch gleich. Aber nach der obigen Verarbeitung kann der übergeordnete Knoten des G-Knotens auch rot sein. Zu diesem Zeitpunkt müssen wir den G-Knoten rekursiv als neuen Knoten behandeln.

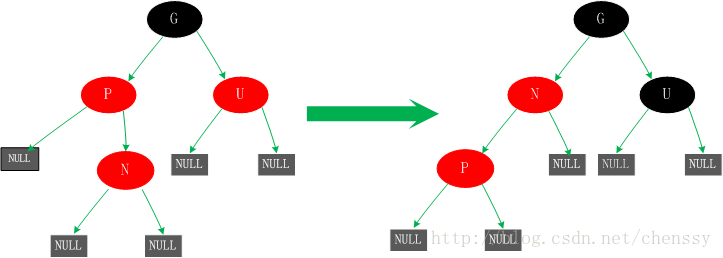
4. Wenn der übergeordnete Knoten P ist rot, der Onkelknoten U ist schwarz oder fehlt und der neue Knoten N ist das rechte Kind des P-Knotens
In diesem Fall führen wir eine Linksdrehung an den neuen Knoten N und P durch. Die hier erzielten Ergebnisse sind tatsächlich nicht vollständig und nicht ausgewogen (ein Verstoß gegen Regel 4). Dies ist, was wir in Fall 5 tun müssen.

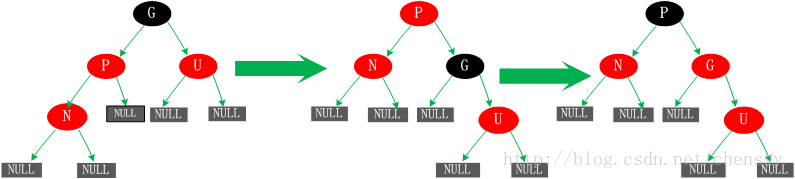
5. Der Elternknoten P ist rot, der Onkelknoten U ist schwarz oder fehlt und der neue Knoten N ist das linke Kind des Elternknotens P
-
Diese Situation kann auf Situation vier zurückzuführen sein, vielleicht aber auch nicht. In diesem Fall wird der P-Knoten zunächst als Mittelpunkt nach rechts gedreht. Im nach der Drehung erzeugten Baum ist der Knoten P der übergeordnete Knoten der Knoten N und G. Dieser Baum ist jedoch nicht standardisiert und verstößt gegen Regel 4. Daher tauschen wir die Farben der P- und G-Knoten aus, damit sie den Spezifikationen entsprechen. Zu Beginn müssen alle Pfade durch G verlaufen und ihre Anzahl an schwarzen Knoten ist gleich, aber jetzt verlaufen alle Pfade durch P und P ist der einzige schwarze Knoten im gesamten Baum, sodass der angepasste Baum auch Spezifikation 5 erfüllt.

Das Obige zeigt die fünf Situationen des Hinzufügens neuer Knoten zum rot-schwarzen Baum Situationen abdecken Mit all den neuen Möglichkeiten kann der Rot-Schwarz-Baum, egal wie komplex er ist, gemäß diesen fünf Situationen generiert werden. Lassen Sie uns analysieren, wie TreeMap in Java rot-schwarze Bäume implementiert.
-
TreeMap put()方法实现分析
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。
对于排序二叉树的创建,其添加节点的过程如下:
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
-
public V put(K key, V value) {
//用t表示二叉树的当前节点
Entry<K,V> t = root;
//t为null表示一个空树,即TreeMap中没有任何元素,直接插入
if (t == null) {
//比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序?
compare(key, key); // type (and possibly null) check
//将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root
root = new Entry<>(key, value, null);
//容器的size = 1,表示TreeMap集合中存在一个元素
size = 1;
//修改次数 + 1
modCount++;
return null;
}
int cmp; //cmp表示key排序的返回结果
Entry<K,V> parent; //父节点
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; //指定的排序算法
//如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合
if (cpr != null) {
do {
parent = t; //parent指向上次循环后的t
//比较新增节点的key和当前节点key的大小
cmp = cpr.compare(key, t.key);
//cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点
if (cmp < 0)
t = t.left;
//cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点
else if (cmp > 0)
t = t.right;
//cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值
else
return t.setValue(value);
} while (t != null);
}
//如果cpr为空,则采用默认的排序算法进行创建TreeMap集合
else {
if (key == null) //key值为空抛出异常
throw new NullPointerException();
/* 下面处理过程和上面一样 */
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//将新增节点当做parent的子节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新增节点的key小于parent的key,则当做左子节点
if (cmp < 0)
parent.left = e;
//如果新增节点的key大于parent的key,则当做右子节点
else
parent.right = e;
/*
* 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置
* 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况
*/
fixAfterInsertion(e);
//TreeMap元素数量 + 1
size++;
//TreeMap容器修改次数 + 1
modCount++;
return null;
}
上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
-
/**
* 新增节点后的修复操作
* x 表示新增节点
*/
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //新增节点的颜色为红色
//循环 直到 x不是根节点,且x的父节点不为红色
while (x != null && x != root && x.parent.color == RED) {
//如果X的父节点(P)是其父节点的父节点(G)的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取X的叔节点(U)
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == rightOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateLeft(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateRight(parentOf(parentOf(x)));
}
}
//如果X的父节点(P)是其父节点的父节点(G)的右节点
else {
//获取X的叔节点(U)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == leftOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateRight(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateLeft(parentOf(parentOf(x)));
}
}
}
//将根节点G强制设置为黑色
root.color = BLACK;
}
-
对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
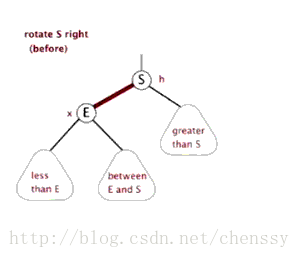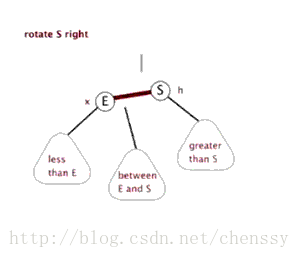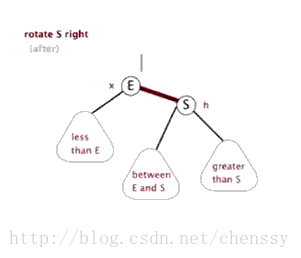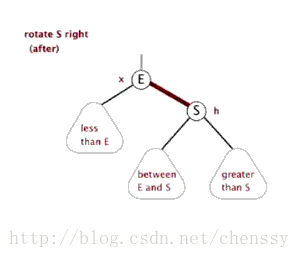
右旋:rotateRight()
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
} 所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}
左旋、右旋的示意图如下:


(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}
四、TreeMap delete()方法
红黑树删除节点
针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。

红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1 Jeder Knoten kann nur rot oder schwarz sein
2. Der Wurzelknoten ist schwarz
3. Jeder Blattknoten (NIL-Knoten, leerer Knoten) ist schwarz.
4. Wenn ein Knoten rot ist, dann hat er zwei Kinder Knoten sind alle schwarz. Das heißt, zwei benachbarte rote Knoten dürfen nicht auf einem Pfad erscheinen.
5. Alle Pfade von jedem Knoten zu jedem seiner Blätter enthalten beide die gleiche Anzahl schwarzer Knoten.
Ich bezweifle, dass Sie für die IT geeignet sind 🎜>
Es stimmt, da das Löschen von Knoten komplizierter ist, einigen wir uns hier auf die Regeln:
1. Der im Folgenden erläuterte gelöschte Knoten muss der Nachfolgeknoten (N) des tatsächlich zu löschenden Knotens sein. wie oben erwähntes C.
2 Die unten genannten Bäume zum Löschen von Knoten haben die folgende Struktur, und die Struktur ist ausgewählt Knoten ist der untergeordnete Knoten ganz links im rechten Baum des zu löschenden Knotens. Hier legen wir fest, dass der tatsächlich gelöschte Knoten N ist, der übergeordnete Knoten P ist, der Geschwisterknoten W ist und die beiden untergeordneten Knoten des Geschwisterknotens X1 und X2 sind. Wie unten gezeigt (2.1).

Jetzt analysieren und bewältigen wir die drei oben genannten Situationen.
Fall 1, kein untergeordneter Knoten (roter Knoten)
In diesem Fall können Sie den Knoten direkt löschen, ohne dass sich dies auf die Struktur des Baums auswirkt. Da der Knoten ein Blattknoten ist, kann er keine untergeordneten Knoten haben. ----- Wenn der untergeordnete Knoten schwarz ist, verstößt er gegen das Prinzip der Anzahl schwarzer Knoten (Bestimmung 5), und wenn er rot ist, verstößt er gegen das „ „Farbe“-Prinzip (Bestimmung 4). Wie in der Abbildung oben (2.2) gezeigt.
Fall 2: Es gibt einen untergeordneten Knoten
Diese Situation ist ebenfalls sehr einfach zu handhaben: Ersetzen Sie einfach den zu löschenden Knoten durch einen untergeordneten Knoten und löschen Sie dann das untergeordnete Element Knoten. Wie im Bild oben (2.3) gezeigt
Fall 3 gibt es zwei untergeordnete Knoten
Diese Situation kann etwas kompliziert sein. Es muss einen alternativen Knoten (N) finden, der gelöscht werden soll, um ihn zu ersetzen, und dann N löschen. Es ist hauptsächlich in vier Situationen unterteilt. 1. Der Geschwisterknoten W von N ist rot
2. Ns Bruder w ist schwarz und die beiden Kinder von w sind beide schwarz.
3. Ns Bruder w ist schwarz, ws linkes Kind ist rot und ws rechtes Kind ist rot Das Kind ist schwarz.
4. Ns Bruder w ist schwarz und ws rechtes Kind ist rot.
Fall 3.1. Der Geschwisterknoten W ist rot
P ist auch schwarz. Die Verarbeitungsstrategie lautet: Ändern Sie die Farbe von W und P und führen Sie dann eine Linksdrehung durch. Durch diese Behandlung bleiben die roten und schwarzen Eigenschaften weiterhin erhalten. Der neue Bruder von N, new w, ist vor der Rotation ein Kind von w und ist schwarz. Nach dieser Behandlung wird die Situation 3.1 in eine der Situationen 3.2, 3.3 und 3.4 umgewandelt. Wie folgt:

Fall 3.2. Ns Bruder w ist schwarz und die beiden Kinder von w sind beide schwarz.
In diesem Fall kann der übergeordnete Knoten rot sein Es kann schwarz sein, was dazu führt, dass der N-Teilbaum einen schwarzen Knoten weniger hat als sein Bruder-W-Teilbaum. Zu diesem Zeitpunkt können wir W auf Rot setzen. Auf diese Weise sind die schwarzen Knoten des N-Teilbaums und des W-Teilbaums konsistent und sorgen für ein Gleichgewicht. Wie folgt

Konvertieren Sie W von Schwarz in Rot, was dazu führt, dass der neue Knoten N einen schwarzen Knoten weniger hat als sein Geschwisterknoten. Wenn das neue x jedoch rot ist, konvertieren wir das neue x direkt in Schwarz, um das Gleichgewicht des gesamten Baums aufrechtzuerhalten. Andernfalls verwandelt sich Situation 3.2 in eine der Situationen 3.1, 3.3 und 3.4.
Fall 3.3, Ns Bruder w ist schwarz, der Linke Das Kind von w ist rot und das rechte Kind von w ist schwarz.
Die untergeordneten Knoten führen einen Farbaustausch durch und führen dann eine Rechtsdrehung auf W durch.

Zu diesem Zeitpunkt ist Ns neuer Bruder X1 (neues w) ein schwarzer Knoten mit einem roten rechten Kind, sodass Situation 3 in Situation 4 umgewandelt wird.
Fall 3.4. Ns Bruder w ist schwarz und w ist das richtige Kind ist rot.
Tauschen Sie die Farben von W und dem übergeordneten Knoten P und führen Sie gleichzeitig eine Linksdrehung an P durch. Dadurch wird der fehlende schwarze Knoten auf der linken Seite ausgefüllt. Setzen Sie gleichzeitig den rechten untergeordneten Knoten X2 von W auf Schwarz. Auf diese Weise wird ein Gleichgewicht zwischen links und rechts erreicht. 
总结
个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。
通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。
TreeMap deleteEntry()方法实现分析
通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
(1)除是寻找替代节点replacement,其实现方法为successor()。如下:
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
(2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下:
1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。
private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
} 这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。
5. Schreiben Sie am Ende
Dieser Blog-Beitrag ist tatsächlich etwas lang. Ich möchte mich bei Ihnen allen dafür bedanken, dass Sie ihn ruhig lesen können Das Lesen dieses Blogbeitrags muss sehr lohnend sein. Gleichzeitig wird in diesem Blog-Beitrag viel Zeit damit verbracht, den Implementierungsprozess von Rot-Schwarz-Bäumen zu erklären, und es wird weniger auf Javas TreeMap eingegangen. Ich denke jedoch, dass Sie es leicht verstehen können, wenn Sie den Implementierungsprozess von Rot-Schwarz-Bäumen verstehen Master TreeMap, was ein Kinderspiel ist.
Gleichzeitig habe ich diesen Blogbeitrag vier Tage lang geschrieben und viel gelesen und referenziert Blogbeiträge. Gleichzeitig ist es unvermeidlich, dass es einige Bezugspunkte gibt, denen ich meinen Dank aussprechen möchte. LZ begann in seinem zweiten Jahr, Datenstrukturen zu lernen. Jetzt habe ich festgestellt, dass ich noch zu viel über Datenstrukturen lernen muss. ! !
Das Obige ist der Inhalt des Java-Verbesserungskapitels (27) -----TreeMap Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.cn). )!
//比较器,因为TreeMap是有序的,通过comparator接口我们可以对TreeMap的内部排序进行精密的控制 private final Comparator99be4058f294b5c4a6207ddd3216ce19 comparator; //TreeMap红-黑节点,为TreeMap的内部类 private transient Entryb77a8d9c3c319e50d4b02a976b347910 root = null; //容器大小 private transient int size = 0; //TreeMap修改次数 private transient int modCount = 0; //红黑树的节点颜色--红色 private static final boolean RED = false; //红黑树的节点颜色--黑色 private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子 Entryb77a8d9c3c319e50d4b02a976b347910 left = null; //右孩子 Entryb77a8d9c3c319e50d4b02a976b347910 right = null; //父亲 Entryb77a8d9c3c319e50d4b02a976b347910 parent; //颜色 boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
三、TreeMap put()方法
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树增加节点
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
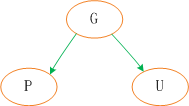
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
-
Wenn der neu eingefügte Knoten N keinen übergeordneten Knoten hat, kann er direkt als Knoten eingefügt werden. Stellen Sie die Farbe auf Schwarz ein. (Wie in Abbildung 1 (1) dargestellt)
2. Der Elternteil Knoten ist schwarz
Rot, da es gemäß Regel 4 zwei schwarze Blattknoten gibt und der Wert ist null. Da der neue Knoten N rot ist, enthält der Pfad durch seine untergeordneten Knoten gleichzeitig immer noch die gleiche Anzahl schwarzer Knoten, was auch Regel 5 erfüllt. (Wie in Abbildung 1 (2) dargestellt)

(Bild 1)3. Wenn der übergeordnete Knoten P und der Geschwisterknoten U beide rot sind
In diesem Fall wird es bei direkter Einfügung definitiv zu einem Ungleichgewicht kommen. Wie damit umgehen? Die P- und U-Knoten werden schwarz und der G-Knoten wird rot. Da die Pfade, die durch die Knoten P und U verlaufen, zu diesem Zeitpunkt durch G verlaufen müssen, ist die Anzahl der schwarzen Knoten auf diesen Pfaden immer noch gleich. Aber nach der obigen Verarbeitung kann der übergeordnete Knoten des G-Knotens auch rot sein. Zu diesem Zeitpunkt müssen wir den G-Knoten rekursiv als neuen Knoten behandeln.

4. Wenn der übergeordnete Knoten P ist rot, der Onkelknoten U ist schwarz oder fehlt und der neue Knoten N ist das rechte Kind des P-Knotens
In diesem Fall führen wir eine Linksdrehung an den neuen Knoten N und P durch. Die hier erzielten Ergebnisse sind tatsächlich nicht vollständig und nicht ausgewogen (ein Verstoß gegen Regel 4). Dies ist, was wir in Fall 5 tun müssen.

5. Der Elternknoten P ist rot, der Onkelknoten U ist schwarz oder fehlt und der neue Knoten N ist das linke Kind des Elternknotens P
-
Diese Situation kann auf Situation vier zurückzuführen sein, vielleicht aber auch nicht. In diesem Fall wird der P-Knoten zunächst als Mittelpunkt nach rechts gedreht. Im nach der Drehung erzeugten Baum ist der Knoten P der übergeordnete Knoten der Knoten N und G. Dieser Baum ist jedoch nicht standardisiert und verstößt gegen Regel 4. Daher tauschen wir die Farben der P- und G-Knoten aus, damit sie den Spezifikationen entsprechen. Zu Beginn müssen alle Pfade durch G verlaufen und ihre Anzahl an schwarzen Knoten ist gleich, aber jetzt verlaufen alle Pfade durch P und P ist der einzige schwarze Knoten im gesamten Baum, sodass der angepasste Baum auch Spezifikation 5 erfüllt.

Das Obige zeigt die fünf Situationen des Hinzufügens neuer Knoten zum rot-schwarzen Baum Situationen abdecken Mit all den neuen Möglichkeiten kann der Rot-Schwarz-Baum, egal wie komplex er ist, gemäß diesen fünf Situationen generiert werden. Lassen Sie uns analysieren, wie TreeMap in Java rot-schwarze Bäume implementiert.
-
TreeMap put()方法实现分析
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
-
public V put(K key, V value) { //用t表示二叉树的当前节点 Entry<K,V> t = root; //t为null表示一个空树,即TreeMap中没有任何元素,直接插入 if (t == null) { //比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序? compare(key, key); // type (and possibly null) check //将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root root = new Entry<>(key, value, null); //容器的size = 1,表示TreeMap集合中存在一个元素 size = 1; //修改次数 + 1 modCount++; return null; } int cmp; //cmp表示key排序的返回结果 Entry<K,V> parent; //父节点 // split comparator and comparable paths Comparator<? super K> cpr = comparator; //指定的排序算法 //如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合 if (cpr != null) { do { parent = t; //parent指向上次循环后的t //比较新增节点的key和当前节点key的大小 cmp = cpr.compare(key, t.key); //cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点 if (cmp < 0) t = t.left; //cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点 else if (cmp > 0) t = t.right; //cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值 else return t.setValue(value); } while (t != null); } //如果cpr为空,则采用默认的排序算法进行创建TreeMap集合 else { if (key == null) //key值为空抛出异常 throw new NullPointerException(); /* 下面处理过程和上面一样 */ Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } //将新增节点当做parent的子节点 Entry<K,V> e = new Entry<>(key, value, parent); //如果新增节点的key小于parent的key,则当做左子节点 if (cmp < 0) parent.left = e; //如果新增节点的key大于parent的key,则当做右子节点 else parent.right = e; /* * 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置 * 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况 */ fixAfterInsertion(e); //TreeMap元素数量 + 1 size++; //TreeMap容器修改次数 + 1 modCount++; return null; } 上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
-
/** * 新增节点后的修复操作 * x 表示新增节点 */ private void fixAfterInsertion(Entry<K,V> x) { x.color = RED; //新增节点的颜色为红色 //循环 直到 x不是根节点,且x的父节点不为红色 while (x != null && x != root && x.parent.color == RED) { //如果X的父节点(P)是其父节点的父节点(G)的左节点 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { //获取X的叔节点(U) Entry<K,V> y = rightOf(parentOf(parentOf(x))); //如果X的叔节点(U) 为红色(情况三) if (colorOf(y) == RED) { //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的叔节点(U)设置为黑色 setColor(y, BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } //如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五) else { //如果X节点为其父节点(P)的右子树,则进行左旋转(情况四) if (x == rightOf(parentOf(x))) { //将X的父节点作为X x = parentOf(x); //右旋转 rotateLeft(x); } //(情况五) //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); //以X的父节点的父节点(G)为中心右旋转 rotateRight(parentOf(parentOf(x))); } } //如果X的父节点(P)是其父节点的父节点(G)的右节点 else { //获取X的叔节点(U) Entry<K,V> y = leftOf(parentOf(parentOf(x))); //如果X的叔节点(U) 为红色(情况三) if (colorOf(y) == RED) { //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的叔节点(U)设置为黑色 setColor(y, BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } //如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五) else { //如果X节点为其父节点(P)的右子树,则进行左旋转(情况四) if (x == leftOf(parentOf(x))) { //将X的父节点作为X x = parentOf(x); //右旋转 rotateRight(x); } //(情况五) //将X的父节点(P)设置为黑色 setColor(parentOf(x), BLACK); //将X的父节点的父节点(G)设置红色 setColor(parentOf(parentOf(x)), RED); //以X的父节点的父节点(G)为中心右旋转 rotateLeft(parentOf(parentOf(x))); } } } //将根节点G强制设置为黑色 root.color = BLACK; } -
对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
右旋:rotateRight()
对于排序二叉树的创建,其添加节点的过程如下:
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
}所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}左旋、右旋的示意图如下:

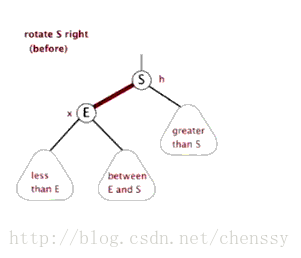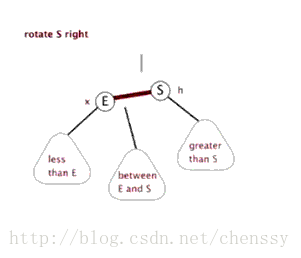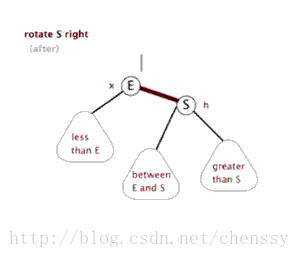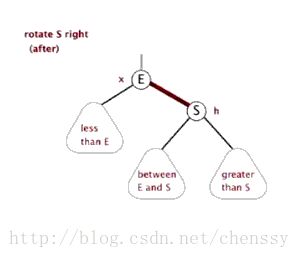
(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}四、TreeMap delete()方法
红黑树删除节点
针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。
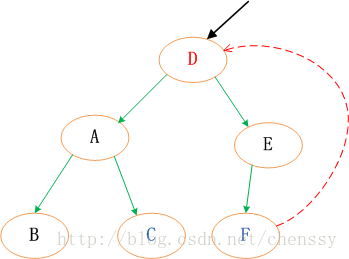
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1 Jeder Knoten kann nur rot oder schwarz sein
2. Der Wurzelknoten ist schwarz
3. Jeder Blattknoten (NIL-Knoten, leerer Knoten) ist schwarz.
4. Wenn ein Knoten rot ist, dann hat er zwei Kinder Knoten sind alle schwarz. Das heißt, zwei benachbarte rote Knoten dürfen nicht auf einem Pfad erscheinen.
5. Alle Pfade von jedem Knoten zu jedem seiner Blätter enthalten beide die gleiche Anzahl schwarzer Knoten.
Ich bezweifle, dass Sie für die IT geeignet sind 🎜>
Es stimmt, da das Löschen von Knoten komplizierter ist, einigen wir uns hier auf die Regeln:
1. Der im Folgenden erläuterte gelöschte Knoten muss der Nachfolgeknoten (N) des tatsächlich zu löschenden Knotens sein. wie oben erwähntes C.
2 Die unten genannten Bäume zum Löschen von Knoten haben die folgende Struktur, und die Struktur ist ausgewählt Knoten ist der untergeordnete Knoten ganz links im rechten Baum des zu löschenden Knotens. Hier legen wir fest, dass der tatsächlich gelöschte Knoten N ist, der übergeordnete Knoten P ist, der Geschwisterknoten W ist und die beiden untergeordneten Knoten des Geschwisterknotens X1 und X2 sind. Wie unten gezeigt (2.1).
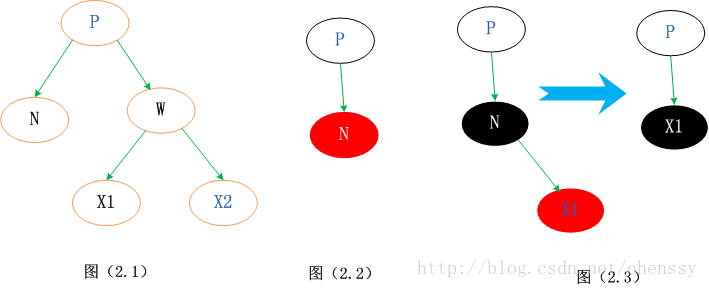
Jetzt analysieren und bewältigen wir die drei oben genannten Situationen.
Fall 1, kein untergeordneter Knoten (roter Knoten)
In diesem Fall können Sie den Knoten direkt löschen, ohne dass sich dies auf die Struktur des Baums auswirkt. Da der Knoten ein Blattknoten ist, kann er keine untergeordneten Knoten haben. ----- Wenn der untergeordnete Knoten schwarz ist, verstößt er gegen das Prinzip der Anzahl schwarzer Knoten (Bestimmung 5), und wenn er rot ist, verstößt er gegen das „ „Farbe“-Prinzip (Bestimmung 4). Wie in der Abbildung oben (2.2) gezeigt.
Fall 2: Es gibt einen untergeordneten Knoten
Diese Situation ist ebenfalls sehr einfach zu handhaben: Ersetzen Sie einfach den zu löschenden Knoten durch einen untergeordneten Knoten und löschen Sie dann das untergeordnete Element Knoten. Wie im Bild oben (2.3) gezeigt
Fall 3 gibt es zwei untergeordnete Knoten
Diese Situation kann etwas kompliziert sein. Es muss einen alternativen Knoten (N) finden, der gelöscht werden soll, um ihn zu ersetzen, und dann N löschen. Es ist hauptsächlich in vier Situationen unterteilt. 1. Der Geschwisterknoten W von N ist rot 2. Ns Bruder w ist schwarz und die beiden Kinder von w sind beide schwarz. 3. Ns Bruder w ist schwarz, ws linkes Kind ist rot und ws rechtes Kind ist rot Das Kind ist schwarz. 4. Ns Bruder w ist schwarz und ws rechtes Kind ist rot. Fall 3.1. Der Geschwisterknoten W ist rot P ist auch schwarz. Die Verarbeitungsstrategie lautet: Ändern Sie die Farbe von W und P und führen Sie dann eine Linksdrehung durch. Durch diese Behandlung bleiben die roten und schwarzen Eigenschaften weiterhin erhalten. Der neue Bruder von N, new w, ist vor der Rotation ein Kind von w und ist schwarz. Nach dieser Behandlung wird die Situation 3.1 in eine der Situationen 3.2, 3.3 und 3.4 umgewandelt. Wie folgt: 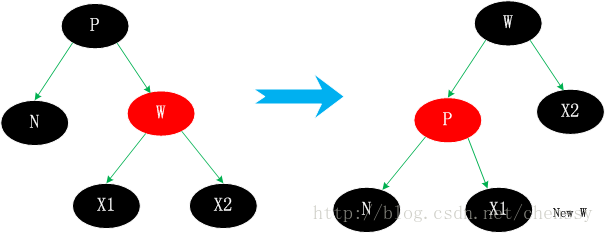
Fall 3.2. Ns Bruder w ist schwarz und die beiden Kinder von w sind beide schwarz.
In diesem Fall kann der übergeordnete Knoten rot sein Es kann schwarz sein, was dazu führt, dass der N-Teilbaum einen schwarzen Knoten weniger hat als sein Bruder-W-Teilbaum. Zu diesem Zeitpunkt können wir W auf Rot setzen. Auf diese Weise sind die schwarzen Knoten des N-Teilbaums und des W-Teilbaums konsistent und sorgen für ein Gleichgewicht. Wie folgt

Konvertieren Sie W von Schwarz in Rot, was dazu führt, dass der neue Knoten N einen schwarzen Knoten weniger hat als sein Geschwisterknoten. Wenn das neue x jedoch rot ist, konvertieren wir das neue x direkt in Schwarz, um das Gleichgewicht des gesamten Baums aufrechtzuerhalten. Andernfalls verwandelt sich Situation 3.2 in eine der Situationen 3.1, 3.3 und 3.4.
Fall 3.3, Ns Bruder w ist schwarz, der Linke Das Kind von w ist rot und das rechte Kind von w ist schwarz.
Die untergeordneten Knoten führen einen Farbaustausch durch und führen dann eine Rechtsdrehung auf W durch.
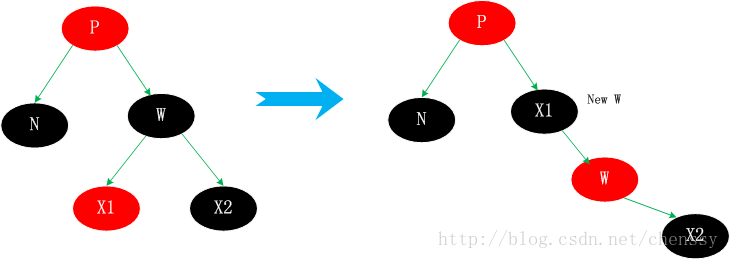
Zu diesem Zeitpunkt ist Ns neuer Bruder X1 (neues w) ein schwarzer Knoten mit einem roten rechten Kind, sodass Situation 3 in Situation 4 umgewandelt wird.
Fall 3.4. Ns Bruder w ist schwarz und w ist das richtige Kind ist rot.
Tauschen Sie die Farben von W und dem übergeordneten Knoten P und führen Sie gleichzeitig eine Linksdrehung an P durch. Dadurch wird der fehlende schwarze Knoten auf der linken Seite ausgefüllt. Setzen Sie gleichzeitig den rechten untergeordneten Knoten X2 von W auf Schwarz. Auf diese Weise wird ein Gleichgewicht zwischen links und rechts erreicht. 总结 个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。 通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。 通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。 (1)除是寻找替代节点replacement,其实现方法为successor()。如下: (2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下: 1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。 2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。 3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。 删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。 这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。 Dieser Blog-Beitrag ist tatsächlich etwas lang. Ich möchte mich bei Ihnen allen dafür bedanken, dass Sie ihn ruhig lesen können Das Lesen dieses Blogbeitrags muss sehr lohnend sein. Gleichzeitig wird in diesem Blog-Beitrag viel Zeit damit verbracht, den Implementierungsprozess von Rot-Schwarz-Bäumen zu erklären, und es wird weniger auf Javas TreeMap eingegangen. Ich denke jedoch, dass Sie es leicht verstehen können, wenn Sie den Implementierungsprozess von Rot-Schwarz-Bäumen verstehen Master TreeMap, was ein Kinderspiel ist. Gleichzeitig habe ich diesen Blogbeitrag vier Tage lang geschrieben und viel gelesen und referenziert Blogbeiträge. Gleichzeitig ist es unvermeidlich, dass es einige Bezugspunkte gibt, denen ich meinen Dank aussprechen möchte. LZ begann in seinem zweiten Jahr, Datenstrukturen zu lernen. Jetzt habe ich festgestellt, dass ich noch zu viel über Datenstrukturen lernen muss. ! ! 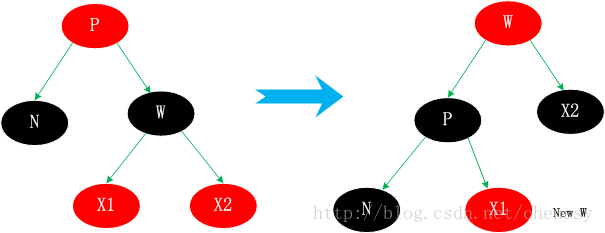
TreeMap deleteEntry()方法实现分析
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
} 5. Schreiben Sie am Ende
Das Obige ist der Inhalt des Java-Verbesserungskapitels (27) -----TreeMap Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.cn). )!