Dynamische Programmierung des PHP-Algorithmus-Lernens (2)

Ich habe das Konzept und die Lösungsschritte der dynamischen Programmierung zuvor kurz vorgestellt, aber während meines Studiums hatte ich das Gefühl, dass der Anwendungsbereich der dynamischen Programmierung zu flexibel ist. Hier werde ich einige häufig gestellte Fragen auswählen und mehr üben.

1. Längste gemeinsame Teilsequenz (stringbezogen)

Suchen Sie bei zwei gegebenen Strings die längste gemeinsame Teilsequenz (LCS) und geben Sie die Länge von LCS zurück. Zum Beispiel:
Zum Beispiel: Bei „ABCD“ und „EDCA“ ist der LCS „A“ (oder D oder C), return 1;
bei „ABCD“ und „EACB“ ist der LCS „ AC“ gibt 2 zurück.

Idee: String a der Länge m und String b der Länge n, ihre längste gemeinsame Teilsequenz longest[m][n] kann durch a und n-1 der Länge m-1 geleitet werden. Die Länge b wird abgeleitet : wenn a[m] gleich b[n] ist, longest[m][n] = longest[m-1][n-1] + 1; wenn a[m] nicht gleich b[n] ist, längste[m][n]=max(längste[m-1][n], längste[m][n-1]). Wenn String a oder b ein leerer String ist, muss die längste gemeinsame Teilsequenz zwischen ihm und dem anderen String 0 sein. Die Lösung der letzten Frage lautet longest[strlen(a)][strlen(b)].
Code:

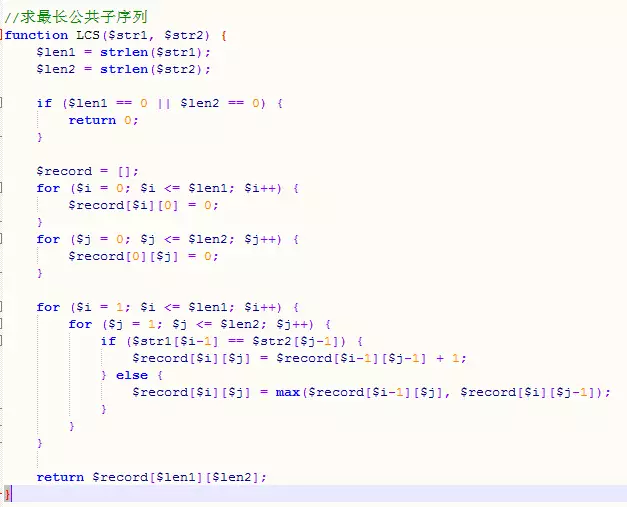
2. Abstand bearbeiten (stringbezogen)

Berechnen Sie bei zwei Wörtern Wort1 und Wort2 die Mindestanzahl an Operationen für Wort2.
Sie haben insgesamt drei Bedienungsmethoden: ein Zeichen einfügen, ein Zeichen löschen und ein Zeichen ersetzen.
Zum Beispiel: Wenn work1="mart" und work2="karma" angegeben sind, wird 3 zurückgegeben.

Idee: Für eine Zeichenfolge a der Länge m und eine Zeichenfolge b der Länge n (sowohl m als auch n sind größer als 0) gilt: Wenn a[m] nicht gleich b[n] ist, wird a zu b Die minimale Anzahl von Operationen = min (die minimale Anzahl von Operationen, damit a[m-1] zu b[n]+1 wird, die minimale Anzahl von Operationen, damit a[m] zu b[n-1]+1 wird , a[m-1 ] wird zu b[n-1]); wenn a[m] gleich b[n] ist, dann wird a[m] zu b[n]. 1] wird zur minimalen Anzahl von Operationen für b[n-1].
Code:

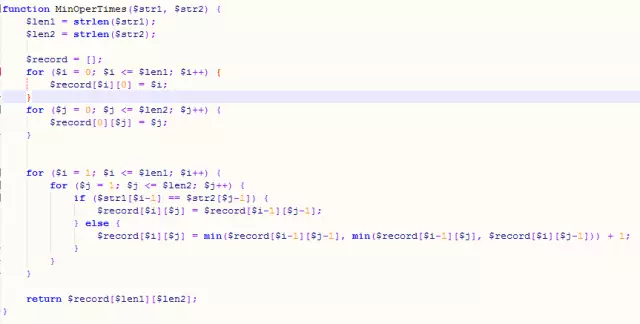
3. Rucksackproblem

Gegeben das Volumen A[i] und der Wert V[i] von n Elementen, Was ist das? Maximaler Gesamtwert, den sie in einen Rucksack der Größe M stecken können?
Zum Beispiel: Für das Artikelvolumen [2, 3, 5, 7] und den entsprechenden Wert [1, 5, 2, 4] beträgt der maximale Wert, der geladen werden kann, unter der Annahme einer Rucksackgröße von 10 9.

Idee: Wenn der Raum v ist und i für jedes Element i eingegeben werden kann (v ist größer oder gleich dem Gewicht [i]), dann ist der Wert f(v) des v-Raums Zu diesem Zeitpunkt ist es gleich f(v -Gewicht[i]) + Werte[i], sodass Sie durch Durchlaufen aller Elemente den Maximalwert ermitteln können, der erhalten werden kann, wenn der Raum v ist.
Code:

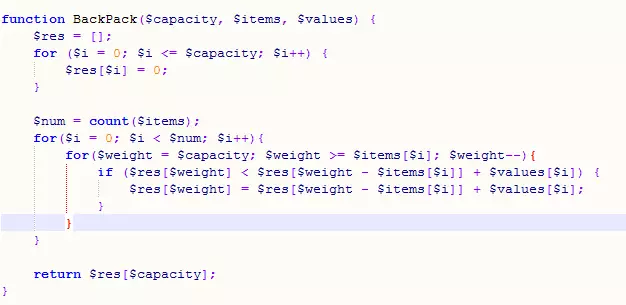
4. Intervallproblem (Google-Interviewfrage)

Es sind n Münzen in einer Reihe aufgereiht, jede Münze hat eine andere Wert. Die beiden Teilnehmer nehmen abwechselnd von beiden Seiten eine Münze, bis keine Münzen mehr übrig sind. Der Gesamtwert der erhaltenen Münzen wird berechnet und diejenige mit dem höchsten Wert gewinnt. Bitte entscheiden Sie, ob der erste Spieler verliert oder gewinnt.
Zum Beispiel: Wenn das Array [3,2,2] gegeben ist, wird true zurückgegeben. Wenn das Array [1,20,15] angegeben ist, wird false zurückgegeben.

Idee: Für ein gegebenes geschlossenes Intervall (i bis j, j ist größer oder gleich i) hat Spieler A nur zwei Möglichkeiten, die Münze zu nehmen, von links oder von rechts. Wenn Sie es von links nehmen, dann ist der maximale Nennwert, den A erhalten kann = der Nennwert der Münze, die Sie erhalten, + der Gesamtnennwert des verbleibenden Intervalls – der maximale Nennwert, den Spieler B im verbleibenden Intervall erhalten kann; Die Situation, in der A es von rechts nimmt, unterscheidet sich von der Situation, in der A es von links nimmt. Nehmen Sie ähnlich. Daraus können wir die Zustandsübergangsgleichung erhalten. Durch zwei Schleifen können wir den Gesamtnennwert eines beliebigen Intervalls von i bis j in der Folge der Länge n sowie den Maximalwert erhalten, den der erste Spieler erhält, wenn j=i (d. h. den Nennwert von i). -te Münze).
Code:

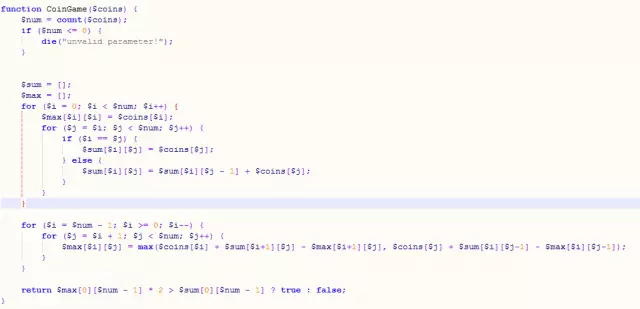
Das Obige ist der Inhalt des dynamischen Programmierens mit PHP-Algorithmen (2). Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.org). .php.cn )!