Selbststudium C#07 von 0 an – Spiralwarteschlange und Spiralbewegung

Realisierung einer Spiralbewegung basierend auf der Logik der Spiralschlange

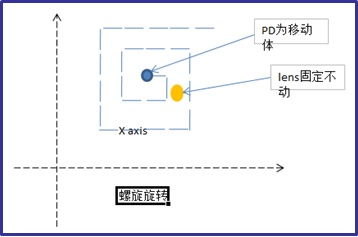
Die umgekehrte Methode des Spiralschlangenalgorithmus steuert den zweiachsigen Motor so, dass er sich entlang einer Spiralbahn bewegt, wie in der Abbildung unten dargestellt.

1. Analyse des Spiral-Warteschlangenalgorithmus

Die folgende Abbildung zeigt eine Spiralwarteschlange. Angenommen, die Koordinaten von 1 sind (0, 0), die x-Richtung ist positiv nach rechts und die y-Richtung ist positiv nach unten. Beispielsweise sind die Koordinaten von 7 (-1, -1) und die Koordinaten von 2 sind (1, 0). Durch die Programmierung können Sie die Koordinaten (x, y) eines beliebigen Punktes eingeben und die entsprechende Zahl ausgeben! (Nachdruck aus dem Internet)

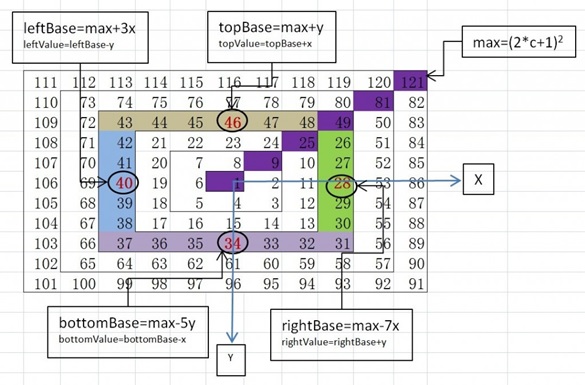
Maximalwert pro Kreis max=(2*c+1)(2*c+1) , c Es ist die Anzahl der Windungen von innen nach außen.

Die Unterschiede zwischen diesen Referenzwerten und Max betragen 1C (oben), 3C (links), 5C (unten), 7C (rechts) (C steht für die aktuelle Rundennummer), oben und unten , y Die Koordinate repräsentiert (oder ist gleich) die Anzahl der Kreise (d. h. C=y), während links und rechts die x-Koordinate die Anzahl der Kreise (d. h. C=x) darstellt (oder gleich ist). Daher kann der zuvor erwähnte Unterschied mithilfe von Koordinaten als 1y, 3x, 5y, 7x ausgedrückt werden.

Code-Implementierung:

private static Object spiral(int x, int y) 
    {  
        int c = max(abs(x), abs(y));// 当前坐标所在圈  
        int max = (c * 2 + 1) * (c * 2 + 1);// 当前圈上最大值  

        if (y == -c) { // 上边  
            return max + (x + y);  
        } else if (x == -c) {// 左边  
            return max + (3 * x - y);  
        } else if (y == c) {// 下边  
            return max + (-x - 5 * y);  
        } else {// 右边  
            return max + (-7 * x + y);  
        }  
    }

2. Spiralbewegung

Passen Sie zunächst die Koordinatenoperation an, um die logische Position von PD darzustellen.

struct Coordinate
    {        public int X;        public int Y;        public Coordinate(int a, int b)
        {
            X = a;
            Y = b;
        }        public static bool operator ==(Coordinate loc1, Coordinate loc2)
        {            return (loc1.X == loc2.X) && (loc1.Y == loc2.Y);
        }        public static bool operator !=(Coordinate loc1, Coordinate loc2)
        {            return !(loc1 == loc2);
        }        public override bool Equals(object loc)
        {            return this == (Coordinate)loc;
        }        public override int GetHashCode()
        {            return base.GetHashCode();
        }        public static Coordinate operator -(Coordinate loc1, Coordinate loc2)
        {            return new Coordinate(loc1.X - loc2.X, loc1.Y - loc2.Y);
        }        public static Coordinate operator +(Coordinate loc1, Coordinate loc2)
        {            return new Coordinate(loc1.X + loc2.X, loc1.Y + loc2.Y);
        }        public override string ToString()
        {            return "(" + X + "," + Y + ")";
        }
    }

Verwenden Sie dann die umgekehrte Methode, um die x- und y-Koordinaten basierend auf der Anzahl der Schritte zu berechnen.

public Coordinate ToLocation(int step, int pulse)
        {            
int c = (int)Math.Ceiling((Math.Sqrt(step) - 1) / 2);            
int max = (int)Math.Pow(2 * c + 1, 2);            
int x, y;

            y = -c;//top
            x = -(max + y - step);            
if (Math.Abs(x) <= Math.Abs(y))
            {                
this.location.X = x * pulse;                
this.location.Y = y * pulse;                
return this.location;
            }

            x = -c;//left
            y = max + 3 * x - step;            
if (Math.Abs(y) <= Math.Abs(x))
            {                
this.location.X = x * pulse;                
this.location.Y = y * pulse;                
return this.location;
            }

            y = c;//bottom
            x = max - 5 * y - step;            
if (Math.Abs(x) <= Math.Abs(y))
            {                
this.location.X = x * pulse;                
this.location.Y = y * pulse;                
return this.location;
            }

            x = c;//right
            y = -(max - 7 * x - step);            
this.location.X = x * pulse;            
this.location.Y = y * pulse;            
//LocChange();
            return this.location;
        }

Schließlich wird die Bewegung entsprechend der Koordinatenänderung realisiert.

public void Start()
        {
            Coordinate moveToLoc, currentLoc, deltaLoc;            

            currentLoc = ToLocation(1, 0);
            logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the start location is ", currentLoc.ToString());
            log.SaveLogToTxt(logInfo);

            logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "begin to move... ");
            log.SaveLogToTxt(logInfo);

            for (int step = 1; step <= this.roMaxStep[0]; step++)
            {
                moveToLoc = ToLocation(step + 1, this.roPulse[0]);
                deltaLoc = moveToLoc - currentLoc;

                logInfo = string.Format("{0}: step{1}{2}{3}...", DateTime.Now.ToString("HH:mm:ss"), step + " ", "move to ", moveToLoc.ToString());
                log.SaveLogToTxt(logInfo);

                bool moveX = card.MoveX(deltaLoc.X);
                bool moveY = card.MoveY(deltaLoc.Y);

                if (moveX == false || moveY == false)
                    //throw error
                    return;

                currentLoc = moveToLoc;                
                //if RES > RoRESTarget
                //break;
            }

            logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "move done");
            log.SaveLogToTxt(logInfo);

            logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the current location is ", currentLoc.ToString());
            log.SaveLogToTxt(logInfo);
        }

Das Obige ist der Inhalt des Selbststudiums C#07 von 0-Spiral Queue und Spiral Movement. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website (www.php.cn). !