Heim >Java >javaLernprogramm >Grafische Erläuterung der Implementierung des QuickSort-Schnellsortieralgorithmus in Java
Grafische Erläuterung der Implementierung des QuickSort-Schnellsortieralgorithmus in Java
- 高洛峰Original
- 2017-01-19 09:13:011550Durchsuche
Im Vergleich zu Algorithmen wie Blasensortierung und Auswahlsortierung sind das spezifische Algorithmusprinzip und die Implementierung der Schnellsortierung etwas schwierig. Um die schnelle Sortierung besser zu verstehen, beschreiben wir das Algorithmusprinzip der schnellen Sortierung noch ausführlich in Form von Beispielen. Im vorherigen Sortieralgorithmus haben wir zur Erläuterung das Größensortierungsproblem von 5 Athleten verwendet. Um die Eigenschaften der schnellen Sortierung besser widerzuspiegeln, fügen wir hier 3 zusätzliche Athleten hinzu. Die Details der acht Athleten im Beispiel und ihre Größeninformationen lauten wie folgt (F, G und H sind neue Athleten): A(181), B(169), C(187), D(172), E( 163), F(191), G(189), H(182)
Im vorherigen Sortieralgorithmus wurden diese Sortierungen vom Trainer durchgeführt. Da die Anzahl der Athleten nun gestiegen ist, möchte der Trainer auch Um die Gelegenheit zu nutzen und eine Pause einzulegen, rief der Trainer zwei Assistenten und bat sie, die Körpergrößen der acht Athleten mithilfe der Schnellsortierungsmethode von links nach rechts und von niedrig nach hoch zu sortieren.
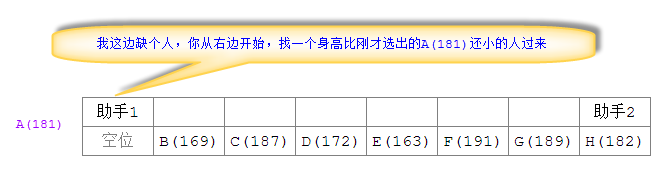
Gemäß dem Algorithmusprinzip der Schnellsortiermethode stehen zwei Assistenten auf beiden Seiten der Athletenanordnung, wie in der Abbildung unten gezeigt

Zuerst Assistent 1 beginnt mit Wählen Sie einen Athleten aus der Anordnung (normalerweise der erste Athlet links oder der mittlere Athlet), hier wählen Sie Athlet A (181). Da die Sortierung von links nach rechts und von niedrig nach hoch erfolgt, benötigt Assistent 1 als Vergleichsmaßstab einen Athleten, dessen Körpergröße kleiner als A(181) ist. Alle Vergleiche in dieser Runde beziehen sich auf Initially ausgewählter Sportler A (181) Vergleich):
Schauen wir uns weiterhin das detaillierte Diagramm der ersten Runde der Schnellsortierung an.
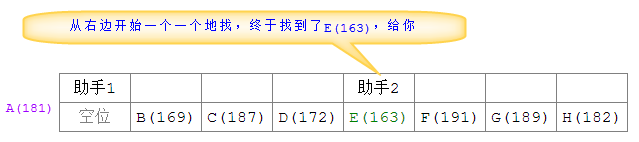


Als zwei Assistenten sortierten und suchten Nachdem Sie sich während des Vorgangs getroffen haben, stoppen Sie den Vergleich der aktuellen Runde und platzieren Sie den ursprünglich ausgewählten Athleten A (181) in dem leeren Feld, in dem sich die beiden Assistenten treffen.
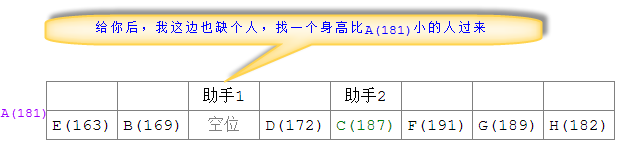
Beim Schnellsortieren treffen sich die beiden Assistenten in dieser Runde Das Sortieren ist vorbei. Zu diesem Zeitpunkt stellen wir fest, dass die Position A (181), an der sich die beiden Athleten treffen, als Trennpunkt verwendet wird. Auf der linken Seite der Anordnung sind alle Athleten kleiner als A (181), und auf der rechten Seite sind alle Athleten kleiner als A (181). Seite der Vereinbarung sind alle Athleten mit einer Körpergröße größer als A(181) Athlet. Zu diesem Zeitpunkt betrachten wir die beiden Sortierungen auf der linken und rechten Seite von A(181) getrennt. Wenn wir weiterhin die Sortiermethoden der beiden oben genannten Assistenten verwenden, um die Anordnungen auf beiden Seiten zu sortieren, dann nach mehreren Anordnungen , Endlich Wir können die Sortierergebnisse erhalten, die wir benötigen.
Das Obige ist der gesamte Sortierimplementierungsprozess der Schnellsortierung. Die schnelle Sortierung verwendet die oben genannten Sortierregeln, um eine Anordnung in zwei Anordnungen und zwei Anordnungen in vier Anordnungen zu unterteilen, bis keine Anordnungen mehr zu trennen sind, und schließlich erhalten wir das Sortierergebnis, das wir benötigen.
Jetzt programmieren wir noch Java-Code, um mithilfe der Schnellsortierung die Körpergrößen der oben genannten 8 Athleten zu sortieren:
/**
* 对指定的数组中索引从start到end之间的元素进行快速排序
*
* @param array 指定的数组
* @param start 需要快速排序的数组索引起点
* @param end 需要快速排序的数组索引终点
*/
public static final void quickSort(int[] array, int start, int end) {
// i相当于助手1的位置,j相当于助手2的位置
int i = start, j = end;
int pivot = array[i]; // 取第1个元素为基准元素
int emptyIndex = i; // 表示空位的位置索引,默认为被取出的基准元素的位置
// 如果需要排序的元素个数不止1个,就进入快速排序(只要i和j不同,就表明至少有2个数组元素需要排序)
while (i < j) {
// 助手2开始从右向左一个个地查找小于基准元素的元素
while (i < j && pivot <= array[j])
j--;
if (i < j) {
// 如果助手2在遇到助手1之前就找到了对应的元素,就将该元素给助手1的"空位",j成了空位
array[emptyIndex] = array[emptyIndex = j];
}
// 助手1开始从左向右一个个地查找大于基准元素的元素
while (i < j && array[i] <= pivot)
i++;
if (i < j) {
// 如果助手1在遇到助手2之前就找到了对应的元素,就将该元素给助手2的"空位",i成了空位
array[emptyIndex] = array[emptyIndex = i];
}
}
// 助手1和助手2相遇后会停止循环,将最初取出的基准值给最后的空位
array[emptyIndex] = pivot;
// =====本轮快速排序完成=====
// 如果分割点i左侧有2个以上的元素,递归调用继续对其进行快速排序
if (i - start > 1) {
quickSort(array, 0, i - 1);
}
// 如果分割点j右侧有2个以上的元素,递归调用继续对其进行快速排序
if (end - j > 1) {
quickSort(array, j + 1, end);
}
}
//主方法
public static void main(String[] args) {
// =====使用快速排序法对表示8名运动员身高的数组heights进行从低到高的排序=====
// A(181)、B(169)、C(187)、D(172)、E(163)、F(191)、G(189)、H(182)
int[] heights = { 181, 169, 187, 172, 163, 191, 189, 182 };
// 调用快速排序方法
quickSort(heights, 0, heights.length - 1);
// 输出排序后的结果
for (int height : heights) {
System.out.println(height);
}
}Die Ausgabe des obigen Java-Codes lautet wie folgt:
163 169 172 181 182 187 189 191
Hinweis: Aufgrund lokaler Denkunterschiede kann es mehrere Variationen der oben genannten schnellen Sortiercode-Implementierung geben. Unabhängig von der Variationsform ändert sich jedoch nichts am Kerngedanken der schnellen Sortierung.
Eine andere Implementierung: Einweg-Scan
Es gibt eine andere Version des Einweg-Scans für die schnelle Sortierung des Arrays. Die spezifischen Schritte bestehen darin, das letzte Element im Array als Teilungselement auszuwählen und festzulegen Dasselbe Zwei Zeiger, Zeiger i zeigt auf die Position vor dem ersten Element im Array und Zeiger j zeigt auf das erste Element im Array. j scannt von vorne nach rechts und von links nach rechts und erhöht i um eins, wenn es auf ein Element trifft, das kleiner oder gleich dem geteilten Element ist, und tauscht dann die Elemente aus, auf die i und j zeigen. Zum Schluss tauschen Sie das Element an Position i+1 mit dem geteilten Element aus, um eine Array-Aufteilung abzuschließen. Der Code ist wie folgt implementiert:
int partition(int[] a, int lo, int hi) {
int i = lo - 1, j = lo;
int v = a[hi];
while (j < hi) {
if (a[j] <= v) {
swap(a, ++i, j);
}
j++;
}
swap(a, i + 1, hi);
return i + 1;
}Weitere Bilder und Texte, die die Methode zur Implementierung des QuickSort-Schnellsortieralgorithmus in Java erläutern, finden Sie auf der chinesischen PHP-Website für verwandte Artikel!
In Verbindung stehende Artikel
Mehr sehen- Wie können Java-Assertions die Codequalität verbessern und Fehler verhindern?
- Beeinflusst die Deklaration von Strings als „final' in Java „=='-Vergleiche?
- String-Manipulation in Java
- Wie aktualisiere ich JLabel kontinuierlich mit den Ergebnissen einer lang andauernden Aufgabe?
- Wie konvertiere ich int[] in Integer[] zur Verwendung als Map-Schlüssel in Java?

