Ausführliche Erläuterung des Bearbeitungsabstands bei der Python-Textähnlichkeitsberechnung

Abstand bearbeiten

Abstand bearbeiten (Abstand bearbeiten), auch Levenshtein-Abstand genannt, bezieht sich auf die Umrechnung zweier Zeichenfolgen von einer zur anderen Mindestzahl der erforderlichen Bearbeitungsvorgänge. Zu den Bearbeitungsvorgängen gehören das Ersetzen eines Zeichens durch ein anderes, das Einfügen eines Zeichens und das Löschen eines Zeichens. Im Allgemeinen gilt: Je kleiner der Bearbeitungsabstand, desto größer die Ähnlichkeit zwischen zwei Zeichenfolgen.

Umwandeln Sie beispielsweise das Wort „kitten“ in „sitting“ um: (Der Bearbeitungsabstand zwischen „kitten“ und „sitting“ beträgt 3)

sitten (k →s)

sittin (e→i)

sitzend (→g)

in Python Das Levenshtein-Paket kann den Bearbeitungsabstand leicht berechnen

Installation des Pakets: pip install python-Levenshtein<code>pip install python-Levenshtein<br>

Verwenden wir it:

# -*- coding:utf-8 -*-
import Levenshtein
texta = '艾伦 图灵传'
textb = '艾伦•图灵传'
print Levenshtein.distance(texta,textb)

Das Ausführungsergebnis des obigen Programms ist 3, aber nur ein Zeichen wurde geändert. Warum passiert das?

Der Grund dafür ist, dass Python diese beiden Zeichenfolgen als Zeichenfolgentyp betrachtet und im Zeichenfolgentyp unter der Standardcodierung utf-8 ein chinesisches Zeichen durch drei Bytes dargestellt wird.

Die Lösung besteht darin, die Zeichenfolge in das Unicode-Format zu konvertieren, wodurch das korrekte Ergebnis 1 zurückgegeben wird.

# -*- coding:utf-8 -*-
import Levenshtein
texta = u'艾伦 图灵传'
textb = u'艾伦•图灵传'
print Levenshtein.distance(texta,textb)

Im Folgenden konzentrieren wir uns auf die Funktionen verschiedener Methoden zur Selbstfürsorge:

Levenshtein.distance(str1, str2)

Bearbeiten Sie den Bearbeitungsabstand (auch Levenshtein-Abstand genannt). Es beschreibt die Mindestanzahl von Vorgängen zum Konvertieren einer Zeichenfolge in eine andere. Zu den Vorgängen gehören Einfügen, Löschen und Ersetzen. Algorithmusimplementierung: dynamische Programmierung.

Levenshtein.hamming(str1, str2)

Hamming-Distanz berechnen. Es ist erforderlich, dass str1 und str2 die gleiche Länge haben. Es beschreibt die Anzahl der unterschiedlichen Zeichen an den entsprechenden Positionen zwischen zwei gleichlangen Zeichenfolgen.

Levenshtein.ratio(str1, str2)

Berechnen Sie das Levenstein-Verhältnis. Berechnungsformel r = (sum – ldist) / sum, wobei sich sum auf die Summe der Längen der Zeichenfolgen str1 und str2 bezieht und ldist der Bearbeitungsabstand der Klasse ist. Beachten Sie, dass dies der Klassenbearbeitungsabstand ist. Beim Löschen und Einfügen beträgt der Wert +1, beim Ersetzen jedoch +2.

Levenshtein.jaro(s1, s2)

Die Jaro-Distanz soll verwendet werden, um festzustellen, ob zwei Namen in Gesundheitsakten gleich sind soll für die Volkszählung verwendet werden. Schauen wir uns zunächst die Definition der Jaro-Entfernung an.

Der Jaro-Abstand zweier gegebener Strings S1 und S2 ist:

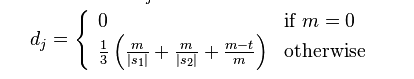
wobei m s1 ist, die Anzahl von Zeichen, die mit s2 übereinstimmen, t ist die Anzahl der Transpositionen.

Wenn der Abstand zwischen zwei Zeichen von S1 und S2 nicht mehr als

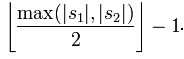
beträgt, gehen wir davon aus, dass diese beiden Zeichenfolgen übereinstimmen Übereinstimmende Zeichen bestimmen die Anzahl der Transpositionen t. Vereinfacht gesagt ist die Hälfte der Anzahl übereinstimmender Zeichen in unterschiedlicher Reihenfolge die Anzahl der Transpositionen t. Beispielsweise stimmen die Zeichen von MARTHA und MARHTA beide überein, aber zwischen diesen übereinstimmenden Zeichen müssen T und H vertauscht werden, um MARTHA in MARHTA umzuwandeln. Dann sind T und H übereinstimmende Zeichen in unterschiedlicher Reihenfolge, t=2/2=1.

Der Jaro-Abstand der beiden Saiten beträgt:

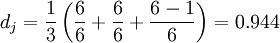
Levenshtein.jaro_winkler(s1, s2)

Berechnen Sie den Jaro-Winkler-Abstand, und Jaro-Winkler gibt Strings mit demselben Startteil eine höhere Punktzahl. Er definiert ein Präfix p und gibt zwei Strings an, wenn der Präfixteil eine Länge von hat gleich, dann ist der Jaro-Winkler-Abstand:

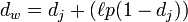
dj ist der Jaro-Abstand der beiden Saiten

ι hat die gleiche Länge wie das Präfix, aber die Höchstgrenze beträgt 4

p ist die Konstante zum Anpassen des Bruchs, die 25 nicht überschreiten darf, andernfalls kann dw größer als 1 sein. Winkler definiert diese Konstante als 0,1

Auf diese Weise beträgt der oben erwähnte Jaro-Winkler-Abstand von MARTHA und MARHTA:

dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961

Persönlich denke ich, dass der Algorithmus verbessert werden kann:

Stoppwörter entfernen (hauptsächlich aufgrund des Einflusses von Satzzeichen)

Chinesisch analysieren und nach Wörtern vergleichen Ist es besser, als mit Worten zu vergleichen?

Zusammenfassung

Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, dass der Inhalt dieses Artikels für jeden, der lernt oder verwendet, hilfreich sein kann Python. Wenn Sie Fragen haben, können Sie eine Nachricht hinterlassen.