Zusammenfassung der zehn wichtigsten Algorithmuskonzepte, die in Vorstellungsgesprächen zur Java-Programmierung häufig verwendet werden

Im Folgenden sind die zehn wichtigsten algorithmusbezogenen Konzepte in Programmierinterviews aufgeführt. Ich werde diese Konzepte anhand einiger einfacher Beispiele veranschaulichen. Da die vollständige Beherrschung dieser Konzepte mehr Aufwand erfordert, dient diese Liste nur als Einführung. In diesem Artikel wird das Problem aus einer Java-Perspektive betrachtet, einschließlich der folgenden Konzepte:

1. String

Wenn die IDE keine Funktion zur automatischen Codevervollständigung hat, sollten Sie Folgendes beachten Methoden.

toCharArray() // 获得字符串对应的char数组
Arrays.sort()  // 数组排序Arrays.toString(char[] a) // 数组转成字符串
charAt(int x) // 获得某个索引处的字符
length() // 字符串长度
length // 数组大小

2. Verknüpfte Liste

In Java ist die Implementierung einer verknüpften Liste sehr einfach. Jeder Knoten Node hat einen Wert val und einen Link next, der auf den nächsten Knoten verweist.

class Node {
    int val;
    Node next;
    Node(int x) {
        val = x;
        next = null;
    }
}

Zwei bekannte Anwendungen verknüpfter Listen sind Stack und Queue.

Stapel:

class Stack{
    Node top; 
    public Node peek(){
        if(top != null){
            return top;
        }
        return null;
    }
    public Node pop(){
        if(top == null){
            return null;
        }else{
            Node temp = new Node(top.val);
            top = top.next;
            return temp;
        }
    }
    public void push(Node n){
        if(n != null){
            n.next = top;
            top = n;
        }
    }
}

Warteschlange:

class Queue{
    Node first, last;
    public void enqueue(Node n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public Node dequeue(){
        if(first == null){
            return null;
        }else{
            Node temp = new Node(first.val);
            first = first.next;
            return temp;
        }
    }
}

3. Baum

Der Baum bezieht sich hier normalerweise auf einen Binärbaum, den jeder Knoten enthält Ein linker untergeordneter Knoten und ein rechter untergeordneter Knoten, wie folgt:

class TreeNode{
    int value;
    TreeNode left;
    TreeNode right;
}

Im Folgenden sind einige Konzepte im Zusammenhang mit Bäumen aufgeführt:

Ausgeglichen vs. unausgeglichen: In jeweils einem ausgeglichenen Binärbaum Knoten Die Tiefen des linken und rechten Teilbaums unterscheiden sich um höchstens 1 (1 oder 0).

Vollständiger Binärbaum: Jeder Knoten außer den Blattknoten hat zwei untergeordnete Knoten.

Perfekter Binärbaum: Es handelt sich um einen vollständigen Binärbaum mit den folgenden Eigenschaften: Alle Blattknoten haben die gleiche Tiefe oder befinden sich auf der gleichen Ebene, und jeder übergeordnete Knoten muss zwei untergeordnete Knoten haben.

Vollständiger Binärbaum: In einem Binärbaum ist jede Ebene außer vielleicht der letzten vollständig gefüllt und alle Knoten müssen so nah wie möglich links liegen.

Anmerkung des Übersetzers: Ein perfekter Binärbaum wird vage auch als vollständiger Binärbaum bezeichnet. Ein Beispiel für einen perfekten Binärbaum ist das Abstammungsdiagramm einer Person in einer bestimmten Tiefe, da jede Person zwei leibliche Eltern haben muss. Ein vollständiger Binärbaum kann als perfekter Binärbaum betrachtet werden, der eine Reihe zusätzlicher, nach links geneigter Blattknoten haben kann. Frage: Was ist der Unterschied zwischen einem perfekten Binärbaum und einem vollständigen Binärbaum? (Referenz: http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html)

4. Diagramm

Diagrammbezogene Probleme konzentrieren sich hauptsächlich auf die Suche nach Tiefe und Breite suchen.

Das Folgende ist eine einfache Implementierung der Graphenbreitensuche.

1) Definieren Sie GraphNode

class GraphNode{ 
    int val;
    GraphNode next;
    GraphNode[] neighbors;
    boolean visited;
    GraphNode(int x) {
        val = x;
    }
    GraphNode(int x, GraphNode[] n){
        val = x;
        neighbors = n;
    }
    public String toString(){
        return "value: "+ this.val; 
    }
}

2) Definieren Sie eine Warteschlange Queue

class Queue{
    GraphNode first, last;
    public void enqueue(GraphNode n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public GraphNode dequeue(){
        if(first == null){
            return null;
        }else{
            GraphNode temp = new GraphNode(first.val, first.neighbors);
            first = first.next;
            return temp;
        }
    }
}

3) Verwenden Sie die Warteschlange Queue, um die Breitensuche zu implementieren

public class GraphTest {
    public static void main(String[] args) {
        GraphNode n1 = new GraphNode(1); 
        GraphNode n2 = new GraphNode(2); 
        GraphNode n3 = new GraphNode(3); 
        GraphNode n4 = new GraphNode(4); 
        GraphNode n5 = new GraphNode(5); 
        n1.neighbors = new GraphNode[]{n2,n3,n5};
        n2.neighbors = new GraphNode[]{n1,n4};
        n3.neighbors = new GraphNode[]{n1,n4,n5};
        n4.neighbors = new GraphNode[]{n2,n3,n5};
        n5.neighbors = new GraphNode[]{n1,n3,n4};
        breathFirstSearch(n1, 5);
    }
    public static void breathFirstSearch(GraphNode root, int x){
        if(root.val == x)
            System.out.println("find in root");
        Queue queue = new Queue();
        root.visited = true;
        queue.enqueue(root);
        while(queue.first != null){
            GraphNode c = (GraphNode) queue.dequeue();
            for(GraphNode n: c.neighbors){
                if(!n.visited){
                    System.out.print(n + " ");
                    n.visited = true;
                    if(n.val == x)
                        System.out.println("Find "+n);
                    queue.enqueue(n);
                }
            }
        }
    }
}

Ausgabe:

1 Wert: 2 Wert: 3 Wert: 5 Wert finden: 5

2 Wert: 4

5. Sortieren

Das Folgende ist die zeitliche Komplexität verschiedener Sortieralgorithmen. Sie können sich im Wiki die Grundideen dieser Algorithmen ansehen.

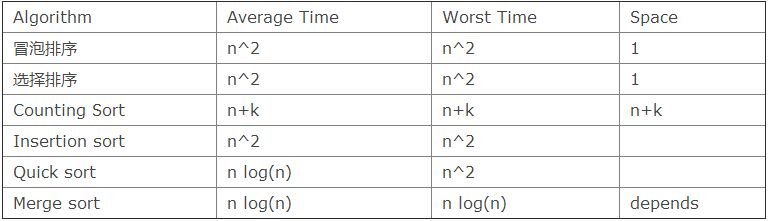
Außerdem finden Sie hier einige Implementierungen/Demos: Counting Sort, Mergesort, Quicksort, InsertionSort.

"Visuelle und intuitive Erfahrung von 7 häufig verwendeten Sortieralgorithmen"

"Video: Demonstration von 15 Sortieralgorithmen in 6 Minuten"

6. Rekursion vs. Iteration

Für Programmierer sollte Rekursion ein eingebauter Gedanke sein, der anhand eines einfachen Beispiels veranschaulicht werden kann.

Frage: Es gibt n Stufen und man kann jeweils nur 1 oder 2 Stufen hinaufgehen. Wie viele Wege gibt es?

Schritt 1: Finden Sie die Beziehung zwischen den ersten n Schritten und den ersten n-1 Schritten.

Um n Stufen hinaufzugehen, gibt es nur zwei Möglichkeiten: 1 Stufe von n-1 Stufen hinaufsteigen, um dorthin zu gelangen, oder 2 Stufen von n-2 Stufen hinaufsteigen, um dorthin zu gelangen. Wenn f(n) die Anzahl der Aufstiegswege zur n-ten Stufe ist, dann ist f(n) = f(n-1) + f(n-2).

Schritt 2: Stellen Sie sicher, dass die Startbedingung korrekt ist.

f(0) = 0;
f(1) = 1;

public static int f(int n){
    if(n <= 2) return n;
    int x = f(n-1) + f(n-2);
    return x;
}

Die zeitliche Komplexität der rekursiven Methode ist in n exponentiell, da es viel Redundanz gibt Berechnet wie folgt:

f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)

Die einfache Idee besteht darin, Rekursion in Iteration umzuwandeln:

public static int f(int n) {
    if (n <= 2){
        return n;
    }
    int first = 1, second = 2;
    int third = 0;
    for (int i = 3; i <= n; i++) {
        third = first + second;
        first = second;
        second = third;
    }
    return third;
}

In diesem Beispiel nimmt die Iteration weniger Zeit in Anspruch. Möglicherweise möchten Sie auch „Rekursion anzeigen“ sehen vs. Iteration.

7. Dynamische Programmierung

Dynamische Programmierung ist eine Technik zur Lösung von Problemen der folgenden Art:

Ein Problem kann durch die Lösung kleinerer Teilprobleme gelöst werden (Anmerkung des Übersetzers: Das heißt, die optimale Lösung des Problems enthält die optimale Lösung seiner Unterprobleme, also die optimalen Unterstruktureigenschaften.

Die Lösungen einiger Teilprobleme müssen möglicherweise mehrmals berechnet werden (Anmerkung des Übersetzers: Dies liegt an der Überlappung der Teilprobleme).

Die Lösungen der Teilprobleme werden in einer Tabelle gespeichert, sodass jedes Teilproblem nur einmal berechnet werden muss.

Benötigt zusätzlichen Platz, um Zeit zu sparen.

Das Stufenkletterproblem entspricht vollständig den oben genannten vier Eigenschaften und kann daher durch dynamische Programmierung gelöst werden.

public static int[] A = new int[100];
public static int f3(int n) {
    if (n <= 2)
        A[n]= n;
    if(A[n] > 0)
        return A[n];
    else
        A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
    return A[n];
}

8. Bitoperationen

Bitoperatoren:

获得给定数字n的第i位：(i从0计数并从右边开始)

public static boolean getBit(int num, int i){
    int result = num & (1<<i);
    if(result == 0){
        return false;
    }else{
        return true;
    }

例如，获得数字10的第2位：

i=1, n=10
11010&10=10
10 is not 0, so return true;

9. 概率问题

解决概率相关的问题通常需要很好的规划了解问题（formatting the problem），这里刚好有一个这类问题的简单例子：

一个房间里有50个人，那么至少有两个人生日相同的概率是多少？（忽略闰年的事实，也就是一年365天）

计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里，我们可以计算所有人生日都互不相同的概率，也就是：365/365 * 364/365 * 363/365 * … * (365-49)/365，这样至少两个人生日相同的概率就是1 – 这个值。

public static double caculateProbability(int n){
    double x = 1; 
    for(int i=0; i<n; i++){
        x *=  (365.0-i)/365.0;
    }
    double pro = Math.round((1-x) * 100);
    return pro/100;

calculateProbability(50) = 0.97

10. 排列组合

组合和排列的区别在于次序是否关键。

如果你有任何问题请在下面评论。

参考/推荐资料：
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell