Big-O-Notation und Zeitkomplexität in JavaScript verstehen

Bei der Arbeit mit JavaScript ist das Schreiben von Funktionscode wichtig, aber es ist ebenso wichtig, sicherzustellen, dass er effizient läuft. Hier kommt Big O Notation ins Spiel. Sie bietet eine Möglichkeit zu analysieren, wie die Leistung Ihres Codes mit zunehmender Eingabegröße skaliert, und hilft Ihnen so, optimierte und skalierbare Anwendungen zu schreiben.

In diesem Artikel werden die Grundlagen der Big-O-Notation und häufige Zeitkomplexitäten anhand anfängerfreundlicher Beispiele in JavaScript erläutert

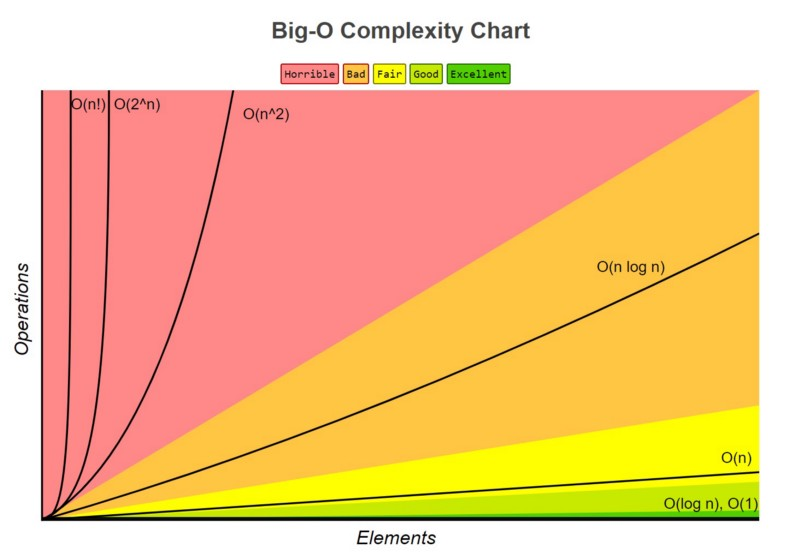
Was ist die Big-O-Notation?

Big O Notation ist eine mathematische Darstellung, die die Effizienz eines Algorithmus beschreibt. Es hilft uns zu verstehen:

1. Zeitkomplexität: Wie sich die Ausführungszeit eines Algorithmus mit der Größe der Eingabe ändert.
2. Raumkomplexität: Wie sich die Speichernutzung eines Algorithmus mit der Größe der Eingabe ändert.

Das Ziel besteht darin, zu bewerten, wie gut ein Algorithmus mit zunehmender Eingabegröße funktioniert, wobei der Schwerpunkt auf Worst-Case-Szenarien liegt.

---

Warum ist die Big-O-Notation wichtig?

Angenommen, Sie haben die Aufgabe, einen Namen in einem Telefonbuch zu finden:

• Eine Möglichkeit besteht darin, jede Seite durchzublättern, bis Sie den Namen gefunden haben (lineare Suche).
• Eine andere Möglichkeit besteht darin, in der Mitte zu beginnen und systematisch einzugrenzen (binäre Suche).

Beide Ansätze lösen das Problem, ihre Effizienz variiert jedoch erheblich, je größer das Telefonbuch wird. Big O hilft uns, diese Ansätze zu vergleichen und den besten auszuwählen.

---

Big-O-Notation in Aktion

Im Folgenden sind häufige Big-O-Komplexitäten aufgeführt, die anhand praktischer Beispiele in JavaScript erläutert werden.

---

1. O(1) – Konstante Zeit

Die Laufzeit bleibt unabhängig von der Eingabegröße gleich. Diese Vorgänge sind die effizientesten.

Beispiel:Zugriff auf ein Element in einem Array über den Index.

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

2. O(log n) – Logarithmische Zeit

Die Laufzeit wächst logarithmisch mit zunehmender Eingabegröße. Dies kommt häufig bei Divide-and-Conquer-Algorithmen wie der binären Suche vor.

Beispiel:Binäre Suche in einem sortierten Array.

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

3. O(n) – Lineare Zeit

Die Laufzeit wächst proportional zur Eingabegröße. Dies geschieht, wenn Sie jedes Element einmal untersuchen müssen.

Beispiel: Suchen eines Elements in einem unsortierten Array.

function linearSearch(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) {
            return i; // Found
        }
    }
    return -1; // Not found
}

const items = [10, 20, 30, 40, 50];
console.log(linearSearch(items, 30)); // Output: 2

---

4. O(n²) – Quadratische Zeit

Die Laufzeit wächst quadratisch mit zunehmender Eingabegröße. Dies ist typisch für Algorithmen mit verschachtelten Schleifen.

Beispiel: Eine grundlegende Implementierung der Blasensortierung.

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

5. O(2ⁿ) – Exponentielle Zeit

Mit jeder weiteren Eingabe verdoppelt sich die Laufzeit. Dies geschieht in Algorithmen, die Probleme rekursiv lösen und dabei alle möglichen Lösungen berücksichtigen.

Beispiel: Rekursive Berechnung von Fibonacci-Zahlen.

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

Visualisierung von Big O

So vergleichen sich verschiedene Big-O-Komplexitäten mit zunehmender Eingabegröße:

Big O	Name	Example Use Case	Growth Rate
O(1)	Constant	Array access	Flat
O(log n)	Logarithmic	Binary search	Slow growth
O(n)	Linear	Looping through an array	Moderate growth
O(n²)	Quadratic	Nested loops	Rapid growth
O(2ⁿ)	Exponential	Recursive brute force	Very fast growth

---

Illustration der Wachstumsraten

Stellen Sie sich vor, Sie lösen ein Problem und die Eingabegröße wächst. So skalieren Algorithmen mit unterschiedlicher Komplexität mit zunehmender Eingabegröße:

Input Size	O(1)	O(log n)	O(n)	O(n²)	O(2ⁿ)
1	1 ms	1 ms	1 ms	1 ms	1 ms
10	1 ms	3 ms	10 ms	100 ms	~1 sec
100	1 ms	7 ms	100 ms	10 sec	~centuries
1000	1 ms	10 ms	1 sec	~17 min	Unrealistic

• O(1) bleibt unabhängig von der Eingabe konstant.
• O(log n) wächst langsam, ideal für große Eingaben.
• O(n) wächst proportional zur Eingabegröße.
• O(n²) und höher werden für große Eingaben schnell unpraktisch.

---

Big O mit Code visualisieren

So visualisieren Sie die Anzahl der Operationen für unterschiedliche Komplexitäten mithilfe einfacher Zähler:

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

Häufige Missverständnisse über Big O

1. Big O ≠ Tatsächliche Leistung: Big O sagt Ihnen, wie die Leistung skaliert, nicht die genaue benötigte Zeit.
   • Zum Beispiel kann ein O(n)-Algorithmus mit einem kleinen konstanten Faktor einen O(log n)-Algorithmus für kleine Eingabegrößen übertreffen.
2. Best-Case vs. Worst-Case: Big O beschreibt normalerweise das Worst-Case-Szenario. Suchen Sie beispielsweise nach einem Element, das nicht in der Liste enthalten ist.
3. Nicht alle verschachtelten Schleifen sind O(n²): Die Komplexität hängt davon ab, wie viele Elemente die innere Schleife verarbeitet.

---

Praktische Tipps für Anfänger

1. Konzentrieren Sie sich auf O(1), O(n) und O(n²): Dies sind die häufigsten Komplexitäten, denen Sie begegnen werden.
2. Leistung messen: Verwenden Sie Tools wie Chrome DevTools, um Ihren Code zu vergleichen.
3. Refactoring für Effizienz: Sobald Ihr Code funktioniert, identifizieren Sie Teile mit höherer Komplexität und optimieren Sie.
4. Lernen Sie weiter: Plattformen wie LeetCode und HackerRank bieten großartige Übungen zum Verständnis von Big O.

---

Abschluss

Big O Notation ist ein wesentliches Werkzeug zur Bewertung der Effizienz von Algorithmen und zum Verständnis der Skalierung Ihres Codes. Wenn Sie die Grundlagen verstehen und gängige Muster analysieren, sind Sie auf dem besten Weg, leistungsstarke JavaScript-Anwendungen zu schreiben.

Viel Spaß beim Codieren! ?

Das obige ist der detaillierte Inhalt vonBig-O-Notation und Zeitkomplexität in JavaScript verstehen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!