Ungerade Ebenen des Binärbaums umkehren

2415. Ungerade Ebenen des Binärbaums umkehren

Schwierigkeit:Mittel

Themen: Baum, Tiefensuche, Breitensuche, Binärbaum

Wenn die Wurzel eines perfekten Binärbaums gegeben ist, kehren Sie die Knotenwerte auf jeder ungerade Ebene des Baums um.

• Angenommen, die Knotenwerte auf Ebene 3 sind [2,1,3,4,7,11,29,18], dann sollte es [18,29,11,7,4,3,1 sein ,2].

Gib die Wurzel des umgekehrten Baums zurück.

Ein Binärbaum ist perfekt, wenn alle übergeordneten Knoten zwei untergeordnete Knoten haben und alle Blätter auf derselben Ebene liegen.

Die Ebene eines Knotens ist die Anzahl der Kanten entlang des Pfades zwischen ihm und dem Wurzelknoten.

Beispiel 1:

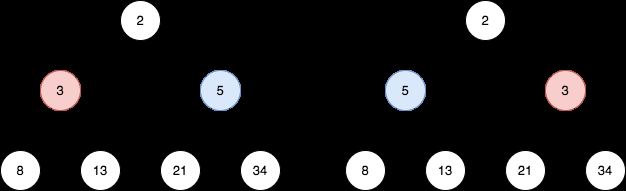
• Eingabe: root = [2,3,5,8,13,21,34]
• Ausgabe: [2,5,3,8,13,21,34]
• Erklärung:
  • Der Baum hat nur eine ungerade Ebene.
  • Die Knoten auf Ebene 1 sind 3 bzw. 5, die umgekehrt werden und zu 5, 3 werden.

Beispiel 2:

• Eingabe: root = [7,13,11]
• Ausgabe: [7,11,13]
• Erklärung:
  • Die Knoten auf Ebene 1 sind 13, 11, die umgekehrt werden und zu 11, 13 werden.

Beispiel 3:

• Eingabe: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
• Ausgabe: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
• Erklärung:
  • Die ungeraden Ebenen haben Werte ungleich Null.
  • Die Knoten auf Ebene 1 waren 1, 2 und sind nach der Umkehrung 2, 1.
  • Die Knoten auf Ebene 3 waren 1, 1, 1, 1, 2, 2, 2, 2 und lauten nach der Umkehrung 2, 2, 2, 2, 1, 1, 1, 1.

Einschränkungen:

• Die Anzahl der Knoten im Baum liegt im Bereich [1, 2¹⁴].
• 0 <= Node.val <= 10⁵
• root ist ein perfekter Binärbaum.

Hinweis:

1. Versuchen Sie, jede Ebene unabhängig voneinander rekursiv zu lösen.
2. Übergeben Sie bei der Durchführung einer Tiefensuche den linken und rechten Knoten (die gepaart werden sollten) an die nächste Ebene. Wenn die aktuelle Ebene ungerade ist, kehren Sie ihre Werte um oder wechseln Sie rekursiv zur nächsten Ebene.

Lösung:

Wir müssen eine Tiefendurchquerung des Binärbaums durchführen. Die Aufgabe besteht darin, die Knotenwerte auf ungeraden Ebenen umzukehren. Ein perfekter Binärbaum bedeutet, dass alle Nicht-Blattknoten zwei untergeordnete Knoten haben und alle Blattknoten auf derselben Ebene liegen.

Wir werden einen DFS-Ansatz (Depth-First Search) verwenden und auf jeder ungeraden Ebene die Knotenwerte umkehren. Nachfolgend finden Sie die Lösung, die dies erreicht.

Kernpunkte:

• Der Baum ist perfekt, das heißt, er ist vollständig ausbalanciert und alle Blattknoten befinden sich auf der gleichen Höhe.
• Nur ​​Knoten auf ungeraden Ebenen müssen umgekehrt werden. Ungerade Ebenen werden ab Ebene 1 (1., 3., 5. usw.) indiziert.
• Ein DFS kann verwendet werden, um den Baum zu durchlaufen und die Knotenebenen zu identifizieren. Wenn wir auf eine ungerade Ebene stoßen, tauschen wir die Werte der Knoten auf dieser Ebene aus.
• Auf jeder Ebene durchlaufen wir zwei untergeordnete Knoten: den linken und den rechten untergeordneten Knoten.

Ansatz:

1. Führen Sie eine Tiefendurchquerung des Baums durch.
2. Für jedes Knotenpaar auf der aktuellen Ebene:
   • Wenn die Ebene ungerade ist, tauschen Sie die Knotenwerte aus.
3. Rekursiv die linken und rechten untergeordneten Elemente des aktuellen Knotens verarbeiten und dabei die aktualisierten Ebeneninformationen übergeben.
4. Gibt den Wurzelknoten zurück, nachdem der gesamte Baum verarbeitet wurde.

Planen:

1. Beginnen Sie mit dem Wurzelknoten.
2. Verwenden Sie eine rekursive Funktion dfs, um den Baum zu durchlaufen und Knotenwerte auf ungeraden Ebenen umzukehren.
3. Behalten Sie den aktuellen Level im Auge, um ungerade Level zu erkennen.
4. Tauschen Sie Werte auf ungeraden Ebenen und setzen Sie die DFS-Durchquerung für die untergeordneten Elemente fort.
5. Geben Sie die Wurzel nach der Verarbeitung zurück.

Lösungsschritte:

1. Definieren Sie eine rekursive Funktion dfs($left, $right, $isOddLevel):
   • left: Linker untergeordneter Knoten.
   • rechts: Rechter untergeordneter Knoten.
   • isOddLevel: Boolescher Wert, der angibt, ob das aktuelle Level ungerade ist.
2. Überprüfen Sie, ob left null ist. Wenn ja, kehren Sie zurück, da keine weiteren Knoten verarbeitet werden müssen.
3. Wenn isOddLevel wahr ist, tauschen Sie die Werte des linken und rechten Knotens aus.
4. Rekursiv die DFS-Funktion aufrufen für:
   • Linkes Kind von links und rechtes Kind von rechts (nächste Ebene).
   • Rechtes Kind von links und linkes Kind von rechts (nächste Ebene).
5. Starten Sie die Rekursion mit dfs($root->left, $root->right, true) und geben Sie die Wurzel zurück.

Lassen Sie uns diese Lösung in PHP implementieren: 2415. Ungerade Ebenen des Binärbaums umkehren


<?php
class TreeNode {
    public $val = 0;
    public $left = null;
    public $right = null;

    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {
    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function reverseOddLevels($root) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * Helper function to perform DFS
     *
     * @param $left
     * @param $right
     * @param $isOddLevel
     * @return void
     */
    private function dfs($left, $right, $isOddLevel) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

// Example usage:
$root = new TreeNode(2);
$root->left = new TreeNode(3);
$root->right = new TreeNode(5);
$root->left->left = new TreeNode(8);
$root->left->right = new TreeNode(13);
$root->right->left = new TreeNode(21);
$root->right->right = new TreeNode(34);

$solution = new Solution();
$reversedRoot = $solution->reverseOddLevels($root);

// Function to print the tree for testing
function printTree($root) {
    if ($root === null) {
        return;
    }
    echo $root->val . " ";
    printTree($root->left);
    printTree($root->right);
}

printTree($reversedRoot); // Output: 2 5 3 8 13 21 34
?>

Erläuterung:

1. TreeNode-Klasse: Stellt die Struktur eines binären Baumknotens dar, der einen Wert (val) und zwei untergeordnete Elemente (links, rechts) hat.
2. reverseOddLevels-Funktion: Initiiert das DFS mit dem linken und rechten untergeordneten Element des Wurzelknotens und beginnt auf Ebene 1 (ungerade Ebene).
3. dfs-Funktion:
   • Berücksichtigt zwei Knoten (links und rechts) und einen booleschen Wert isOddLevel, um zu bestimmen, ob die aktuelle Ebene ungerade ist.
   • Wenn die aktuelle Ebene ungerade ist, werden die Werte von links und rechts vertauscht.
   • Ruft sich selbst rekursiv für die nächste Ebene auf und wechselt dabei den isOddLevel-Wert (wahr wird zu falsch und umgekehrt).
4. Die Rekursion fährt mit der Verarbeitung des nächsten Knotenpaars auf jeder Ebene fort und stellt sicher, dass nur Knoten auf ungeraden Ebenen umgekehrt werden.

Beispielhafte Vorgehensweise:

Beispiel 1:

Eingabe:


       2
      / \
     3   5
    / \ / \
   8 13 21 34

• Stufe 0: [2] (gerade, keine Änderung).
• Stufe 1: [3, 5] (ungerade, umgekehrt zu [5, 3]).
• Stufe 2: [8, 13, 21, 34] (gerade, keine Änderung).

Ausgabe:


       2
      / \
     5   3
    / \ / \
   8 13 21 34

Beispiel 2:

Eingabe:


       7
      / \
     13  11

• Stufe 0: [7] (gerade, keine Änderung).
• Stufe 1: [13, 11] (ungerade, umgekehrt zu [11, 13]).

Ausgabe:


       7
      / \
     11  13

Zeitkomplexität:

• Zeitkomplexität: O(n), wobei n die Anzahl der Knoten im Binärbaum ist. Wir besuchen jeden Knoten genau einmal im Deep-First-Prinzip.
• Raumkomplexität: O(h), wobei h die Höhe des Baums ist. Die Rekursionstiefe entspricht der Höhe des Baums und wäre im schlimmsten Fall (für einen schiefen Baum) O(n), für einen perfekten Binärbaum jedoch O(log n).

Diese Lösung kehrt die Knoten auf ungeraden Ebenen eines perfekten Binärbaums mithilfe einer Tiefensuche mit einer zeitlichen Komplexität von O(n) effizient um. Der Code tauscht Werte auf ungeraden Ebenen aus und verwendet einen rekursiven Ansatz zur Verarbeitung des Baums.

Kontaktlinks

Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, dem Repository einen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!

Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:

• LinkedIn
• GitHub

Das obige ist der detaillierte Inhalt vonUngerade Ebenen des Binärbaums umkehren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!