Heim >Backend-Entwicklung >Python-Tutorial >Batch-, Mini-Batch- und stochastischer Gradientenabstieg
Batch-, Mini-Batch- und stochastischer Gradientenabstieg
- Linda HamiltonOriginal
- 2024-11-24 11:26:09550Durchsuche
Kauf mir einen Kaffee☕
*Memos:
- Mein Beitrag erklärt Batch, Mini-Batch und stochastischen Gradientenabstieg mit DataLoader() in PyTorch.
- Mein Beitrag erklärt Batch Gradient Descent ohne DataLoader() in PyTorch.
- Mein Beitrag erklärt Optimierer in PyTorch.
Es gibt Batch Gradient Descent (BGD), Mini-Batch Gradient Descent (MBGD) und Stochastic Gradient Descent (SGD), die Möglichkeiten sind, Daten aus einem Datensatz zu entnehmen, um einen Gradientenabstieg mit dem durchzuführen Optimierer wie Adam(), SGD(), RMSprop(), Adadelta(), Adagrad() usw. in PyTorch.
*Memos:
- SGD() in PyTorch ist nur der grundlegende Gradientenabstieg ohne besondere Funktionen (klassischer Gradientenabstieg (CGD)), aber kein stochastischer Gradientenabstieg (SGD).
- Mit den folgenden Möglichkeiten können Sie beispielsweise flexibel BGD, MBGD oder SGD Adam mit Adam(), CGD mit SGD(), RMSprop mit RMSprop(), Adadelta mit Adadelta(), Adagrad mit Adagrad(), usw. in PyTorch.
- Grundsätzlich erfolgt BGD, MBGD oder SGD mit gemischten Datensätzen mit DataLoader():
*Memos:
- Das Mischen von Datensätzen verringert die Überanpassung. *Grundsätzlich werden nur Zugdaten gemischt, Testdaten werden also nicht gemischt.
- Mein Beitrag erklärt Overfitting und Underfitting.
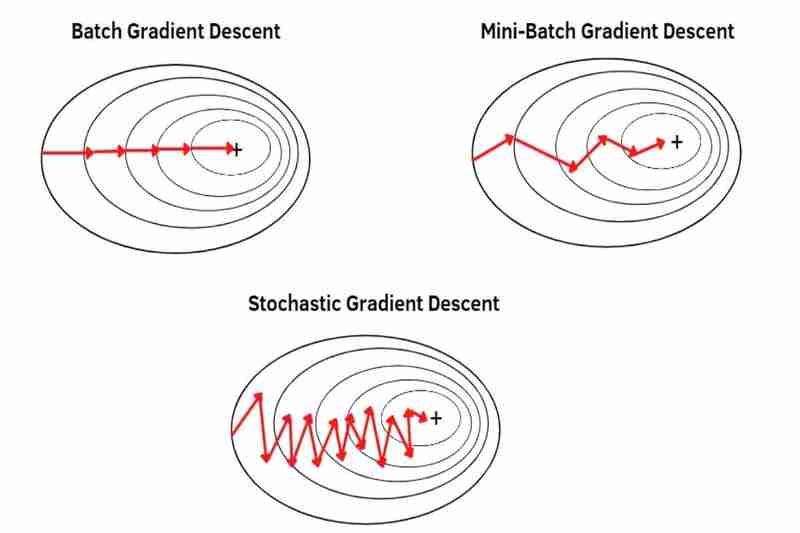
(1) Batch-Gradientenabstieg (BGD):
- kann einen Gradientenabstieg mit einem gesamten Datensatz durchführen und dabei nur einen Schritt in einer Epoche ausführen. Wenn beispielsweise ein ganzer Datensatz 100 Stichproben (1x100) hat, erfolgt der Gradientenabstieg nur einmal in einer Epoche, was bedeutet, dass die Parameter des Modells nur einmal in einer Epoche aktualisiert werden.
- verwendet den Durchschnitt eines gesamten Datensatzes, sodass jede Stichprobe weniger hervorsticht (weniger hervorgehoben) als MBGD und SGD. Infolgedessen ist die Konvergenz stabiler (weniger schwankend) als bei MBGD und SGD und auch stärker im Rauschen (verrauschte Daten) als bei MBGD und SGD, was weniger Überschwingungen als bei MBGD und SGD verursacht und ein genaueres Modell als bei MBGD und SGD erzeugt blieb nicht in lokalen Minima stecken, aber BGD entgeht lokalen Minima oder Sattelpunkten weniger leicht als MBGD und SGD, da die Konvergenz stabiler (weniger schwankend) ist als bei MBGD und SGD Wie ich bereits sagte, verursacht BGD leichter eine Überanpassung als MBGD und SGD, da jede Stichprobe weniger hervorsticht (weniger betont) als MBGD und SGD, wie ich bereits sagte.
*Memos:
- Konvergenz bedeutet, dass sich ein Anfangsgewicht durch Gradientenabstieg in Richtung des globalen Minimums einer Funktion bewegt.
- Rauschen (verrauschte Daten) bedeutet Ausreißer, Anomalien oder manchmal doppelte Daten.
- Überschießen bedeutet das Überspringen des globalen Minimums einer Funktion.
- s Vorteile:
- Die Konvergenz ist stabiler (weniger schwankend) als MBGD und SGD.
- Es ist stärker im Rauschen (verrauschte Daten) als MBGD und SGD.
- Es verursacht weniger Überschwingungen als MBGD und SGD.
- Es erstellt ein genaueres Modell als MBGD und SGD, wenn es nicht in lokalen Minima hängen bleibt.
- s Nachteile:
- Bei einem großen Datensatz wie Online-Lernen ist dies nicht gut, da es viel Speicher beansprucht und die Konvergenz verlangsamt. *Online-Lernen ist die Art und Weise, wie ein Modell schrittweise in Echtzeit aus einem Datensatz lernt.
- Wenn Sie ein Modell aktualisieren möchten, ist die Neuvorbereitung eines gesamten Datensatzes erforderlich.
- Es entgeht lokalen Minima oder Sattelpunkten weniger leicht als MBGD und SGD.
- Es verursacht leichter eine Überanpassung als MBGD und SGD.
(2) Mini-Batch-Gradientenabstieg (MBGD):
- kann einen Gradientenabstieg mit geteilten Datensätzen (den kleinen Stapeln eines gesamten Datensatzes) durchführen, einen kleinen Stapel nach dem anderen, wobei die gleiche Anzahl von Schritten erforderlich ist wie bei den kleinen Stapeln eines gesamten Datensatzes in einer Epoche. Beispielsweise wird der gesamte Datensatz mit 100 Stichproben (1x100) in 5 kleine Stapel (5x20) aufgeteilt, dann erfolgt der Gradientenabstieg fünfmal in einer Epoche, was bedeutet, dass die Parameter des Modells fünfmal in einer Epoche aktualisiert werden.
verwendet den Durchschnitt jeder kleinen Charge, aufgeteilt aus einem gesamten Datensatz, sodass jede Probe stärker hervorgehoben (hervorgehoben) wird als BDG. *Durch die Aufteilung eines gesamten Datensatzes in kleinere Chargen kann jede Probe immer stärker hervorstechen (immer mehr hervorgehoben werden). Infolgedessen ist die Konvergenz weniger stabil (schwankender) als BGD und auch weniger stark im Rauschen (verrauschte Daten) als BGD, was mehr zu Überschwingern als BGD führt und ein weniger genaues Modell als BGD erzeugt, selbst wenn es nicht in lokalen Minima hängen bleibt, sondern MBGD entgeht lokalen Minima oder Sattelpunkten leichter als BGD, weil die Konvergenz weniger stabil ist (stärker schwankt) als BGD, wie ich bereits sagte, und MBGD aufgrund jeder Stichprobe weniger leicht zu einer Überanpassung führt als BGD ist stärker hervorgehoben (betonter) als BGD, wie ich bereits sagte.
-
s Vorteile:
- Bei einem großen Datensatz wie Online-Lernen ist es besser als BGD, da es weniger Speicher benötigt als BGD und die Konvergenz weniger verlangsamt als BGD.
- Es ist nicht die Neuvorbereitung eines gesamten Datensatzes erforderlich, wenn Sie ein Modell aktualisieren möchten.
- Es entgeht lokalen Minima oder Sattelpunkten leichter als BGD.
- Es verursacht weniger leicht eine Überanpassung als BGD.
-
s Nachteile:
- Die Konvergenz ist weniger stabil (schwankender) als BGD.
- Es ist weniger stark im Rauschen (verrauschte Daten) als BGD.
- Es verursacht mehr Überschwingungen als BGD.
- Es erstellt ein weniger genaues Modell als BGD, selbst wenn es nicht in lokalen Minima hängen bleibt.
(3) Stochastischer Gradientenabstieg (SGD):
- kann einen Gradientenabstieg mit jeder einzelnen Stichprobe eines gesamten Datensatzes Stichprobe für Stichprobe durchführen, wobei die gleiche Anzahl von Schritten wie bei den Stichproben eines gesamten Datensatzes in einer Epoche erforderlich ist. Ein ganzer Datensatz hat beispielsweise 100 Stichproben (1x100), dann erfolgt der Gradientenabstieg 100 Mal in einer Epoche, was bedeutet, dass die Parameter des Modells 100 Mal in einer Epoche aktualisiert werden.
verwendet jede einzelne Stichprobe eines gesamten Datensatzes Stichprobe für Stichprobe, jedoch nicht den Durchschnitt, sodass jede Stichprobe stärker hervorgehoben (hervorgehoben) wird als MBGD. Infolgedessen ist die Konvergenz weniger stabil (schwankender) als bei MBGD und auch weniger stark im Rauschen (verrauschte Daten) als bei MBGD, was mehr zu Überschwingern als bei MBGD führt und ein weniger genaues Modell als bei MBGD erzeugt, selbst wenn sie nicht in lokalen Minima hängen bleibt, sondern SGD entgeht lokalen Minima oder Sattelpunkten leichter als MBGD, da die Konvergenz weniger stabil ist (stärker schwankt) als MBGD, wie ich bereits sagte, und SGD aufgrund jeder Stichprobe weniger leicht zu einer Überanpassung führt als MBGD ist, wie ich bereits sagte, auffälliger (hervorgehobener) als MBGD.
-
s Vorteile:
- Bei einem großen Datensatz wie Online-Lernen ist es besser als MBGD, da es weniger Speicher benötigt als MBGD und die Konvergenz weniger verlangsamt als MBGD.
- Es ist nicht die Neuvorbereitung eines gesamten Datensatzes erforderlich, wenn Sie ein Modell aktualisieren möchten.
- Es entgeht lokalen Minima oder Sattelpunkten leichter als MBGD.
- Es verursacht weniger leicht eine Überanpassung als MBGD.
-
s Nachteile:
- Die Konvergenz ist weniger stabil (schwankender) als MBGD.
- Es ist weniger stark im Rauschen (verrauschte Daten) als MBGD.
- Es verursacht mehr Überschwingungen als MBGD.
- Es erstellt ein weniger genaues Modell als MBGD, wenn es nicht in lokalen Minima hängen bleibt.
Das obige ist der detaillierte Inhalt vonBatch-, Mini-Batch- und stochastischer Gradientenabstieg. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

