Big-O-Notation – Python

1. Definition

Mathematische Notation, die die Obergrenze der Ausführungszeit oder des Speicherplatzverbrauchs eines Algorithmus beschreibt. Es wird als O(f(n)) bezeichnet, wobei f(n) eine Funktion ist, die Zeit oder Raum als Funktion der Größe der Eingabe n darstellt .

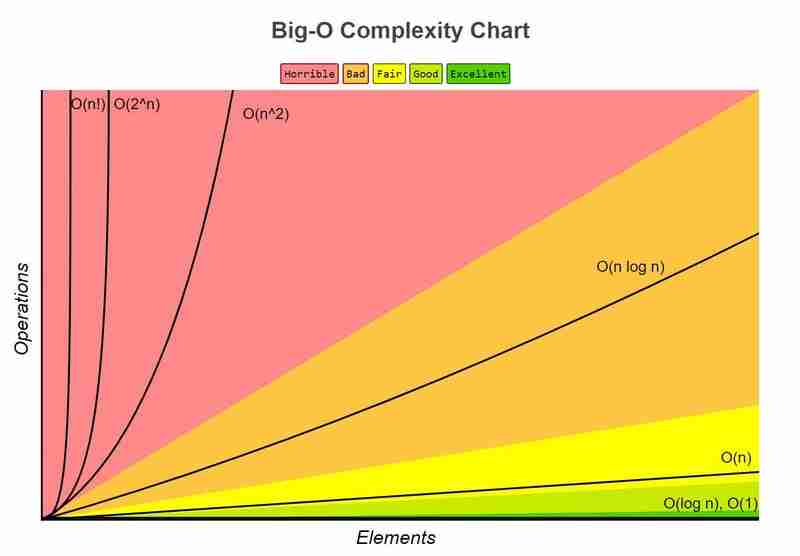
Weitere Informationen finden Sie unter: http://bigochheatsheet.com

2. Zweck

• Algorithmusvergleich: Ermöglicht Ihnen, verschiedene Algorithmen zu vergleichen und den effizientesten für ein bestimmtes Problem auszuwählen.
• Skalierbarkeit: Hilft vorherzusagen, wie sich ein Algorithmus verhält, wenn die Datenmenge zunimmt.

3. Komplexitätsanalyse

• Worst Case: Bezieht sich auf das Szenario, in dem der Algorithmus länger dauert oder mehr Ressourcen verbraucht. Big O bezieht sich normalerweise auf diesen Fall.
• Best Case und Average Case: Obwohl wichtig, werden sie weniger häufig für die Big-O-Notation verwendet.

4. Raum vs. Zeit

• Zeitliche Komplexität: Bezieht sich auf die Zeit, die ein Algorithmus zur Ausführung benötigt.
• Space Complexity: Bezieht sich auf die Menge an zusätzlich genutztem Speicher. Es kann Notationen wie O(1) (konstanter Raum) oder O(n) (linearer Raum) haben.

Beispiel:

import timeit
import matplotlib.pyplot as plt
import cProfile

# O(1)


def constant_time_operation():
    return 42

# O(log n)


def logarithmic_time_operation(n):
    count = 0
    while n > 1:
        n //= 2
        count += 1
    return count

# O(n)


def linear_time_operation(n):
    total = 0
    for i in range(n):
        total += i
    return total

# O(n log n)


def linear_logarithmic_time_operation(n):
    if n <= 1:
        return n
    else:
        return linear_logarithmic_time_operation(n - 1) + n

# O(n^2)


def quadratic_time_operation(n):
    total = 0
    for i in range(n):
        for j in range(n):
            total += i + j
    return total

# O(2^n)


def exponential_time_operation(n):
    if n <= 1:
        return 1
    else:
        return exponential_time_operation(n - 1) + exponential_time_operation(n - 1)

# O(n!)


def factorial_time_operation(n):
    if n == 0:
        return 1
    else:
        return n * factorial_time_operation(n - 1)

# Function to measure execution time using timeit

def measure_time(func, *args):
    execution_time = timeit.timeit(lambda: func(*args), number=1000)
    return execution_time


def plot_results(results):
    functions, times = zip(*results)

    colors = ['skyblue', 'orange', 'green', 'red', 'purple', 'brown', 'pink']
    plt.figure(figsize=(14, 8))
    plt.bar(functions, times, color=colors)

    for i, v in enumerate(times):
        plt.text(i, v + 0.5, f"{v:.6f}", ha='center',
                 va='bottom', rotation=0, color='black')

    plt.xlabel('Function Complexity')
    plt.ylabel('Average Time (s)')
    plt.title('Execution Time of Different Algorithm Complexities')
    plt.grid(axis='y', linestyle='--', linewidth=0.5, color='gray', alpha=0.5)

    plt.tight_layout()
    plt.show()


def main():
    results = []
    results.append(("O(1)", measure_time(constant_time_operation)))
    results.append(("O(log n)", measure_time(logarithmic_time_operation, 10)))
    results.append(("O(n)", measure_time(linear_time_operation, 10)))
    results.append(("O(n log n)", measure_time(
        linear_logarithmic_time_operation, 10)))
    results.append(("O(n^2)", measure_time(quadratic_time_operation, 7)))
    results.append(("O(2^n)", measure_time(exponential_time_operation, 7)))
    results.append(("O(n!)", measure_time(factorial_time_operation, 112)))

    plot_results(results)


if __name__ == '__main__':
    cProfile.run("main()", sort="totime", filename="output_profile.prof")

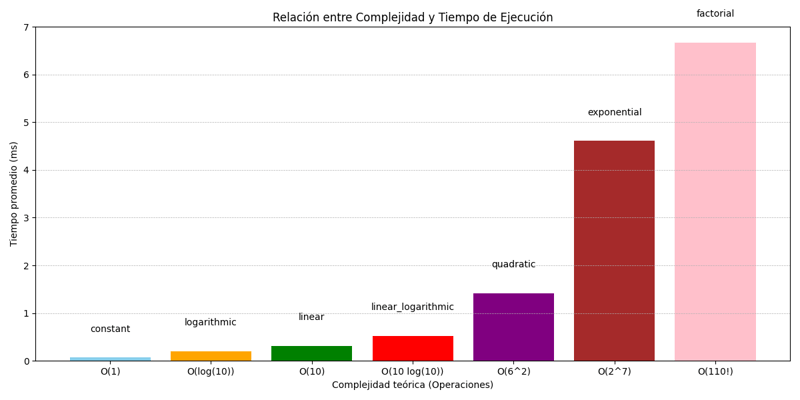
Denken Sie daran, dass es nicht ausreicht, einfach nur die große Notation anzuwenden. Auch wenn dies der erste Schritt ist, gibt es andere Möglichkeiten, den Speicher zu optimieren, zum Beispiel die Verwendung von Slots, Cache, Threads, Parallelität, Prozesse usw.

Danke fürs Lesen!!
Unterstützen Sie mich, indem Sie reagieren und Ihre Meinung äußern.

Das obige ist der detaillierte Inhalt vonBig-O-Notation – Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!