Heim >Web-Frontend >js-Tutorial >Jenseits von JavaScript – Warum es in der Programmierung nicht gleich ist
Jenseits von JavaScript – Warum es in der Programmierung nicht gleich ist
- DDDOriginal
- 2024-09-13 22:17:021048Durchsuche
JavaScript wird häufig lächerlich gemacht, wenn Entwickler zum ersten Mal auf dieses scheinbar verwirrende Ergebnis stoßen:
0.1 + 0.2 == 0.30000000000000004
Memes über den Umgang von JavaScript mit Zahlen sind weit verbreitet, was viele oft zu der Annahme verleitet, dass dieses Verhalten nur in der Sprache vorkommt.
Diese Eigenart ist jedoch nicht nur auf JavaScript beschränkt. Dies ist eine Folge davon, wie die meisten Programmiersprachen mit Gleitkomma-Arithmetik umgehen.
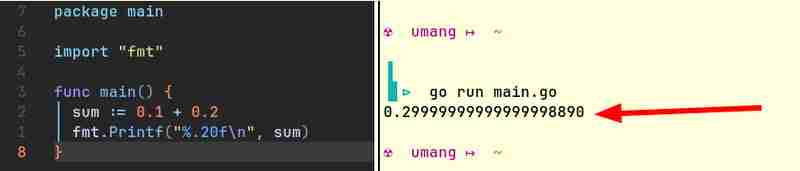
Hier sind zum Beispiel Codeausschnitte aus Java und Go, die ähnliche Ergebnisse liefern:

Computer können nativ nur Ganzzahlen speichern. Sie verstehen keine Brüche. (Wie wollen sie? Computer können nur dann rechnen, wenn sie einige Lichter ein- oder ausschalten. Das Licht kann entweder an oder aus sein. Es kann nicht „halb“ an sein!) Sie brauchen eine Möglichkeit, Gleitkommazahlen darzustellen . Da diese Darstellung nicht ganz genau ist, ist 0,1 0,2 in den meisten Fällen nicht gleich 0,3.
Alle Brüche, deren Nenner aus Primfaktoren der Basis des Zahlensystems bestehen, können sauber ausgedrückt werden, während alle anderen Brüche sich wiederholende Dezimalstellen hätten. Beispielsweise werden im Zahlensystem mit der Basis 10 Brüche wie 1/2, 1/4, 1/5, 1/10 sauber dargestellt, da die Nenner jeweils aus 2 oder 5 – den Primfaktoren von 10 – bestehen . Brüche wie 1/3, 1/6, 1/7 haben jedoch alle wiederkehrende Dezimalstellen.
In ähnlicher Weise werden im Binärsystem Brüche wie 1/2, 1/4, 1/8 sauber ausgedrückt, während alle anderen Brüche wiederkehrende Dezimalstellen haben. Wenn Sie mit diesen wiederkehrenden Dezimalzahlen rechnen, bleiben am Ende Reste übrig, die übertragen werden, wenn Sie die binäre Zahlendarstellung des Computers in eine für Menschen lesbare Basis-10-Darstellung umwandeln. Dies führt zu annähernd korrekten Ergebnissen.
Da wir nun festgestellt haben, dass dieses Problem nicht nur bei JavaScript auftritt, wollen wir untersuchen, wie Gleitkommazahlen unter der Haube dargestellt und verarbeitet werden, um zu verstehen, warum dieses Verhalten auftritt.
Um zu verstehen, wie Gleitkommazahlen unter der Haube dargestellt und verarbeitet werden, müssen wir zunächst den Gleitkommastandard IEEE 754 verstehen.
Der IEEE 754-Standard ist eine weit verbreitete Spezifikation zur Darstellung und Durchführung von Arithmetik auf Gleitkommazahlen in Computersystemen. Es wurde entwickelt, um die Konsistenz bei der Verwendung der Gleitkomma-Arithmetik auf verschiedenen Computerplattformen zu gewährleisten. Die meisten Programmiersprachen und Hardwareimplementierungen (CPUs, GPUs usw.) halten sich an diesen Standard.
So wird eine Zahl im IEEE 754-Format bezeichnet:
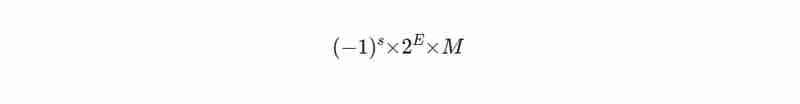
Hier ist s das Vorzeichenbit (0 für positiv, 1 für negativ), M ist die Mantisse (enthält die Ziffern der Zahl) und E ist der Exponent, der die Skalierung der Zahl bestimmt.
Sie könnten keine ganzzahligen Werte für M und E finden, die Zahlen wie 0,1, 0,2 oder 0,3 in diesem Format genau darstellen können. Wir können nur Werte für M und E auswählen, die das nächstgelegene Ergebnis liefern.
Hier ist ein Tool, mit dem Sie die IEEE 754 Notationen von Dezimalzahlen bestimmen können: https://www.h-schmidt.net/FloatConverter/IEEE754.html
IEEE 754 Notation von 0,25:
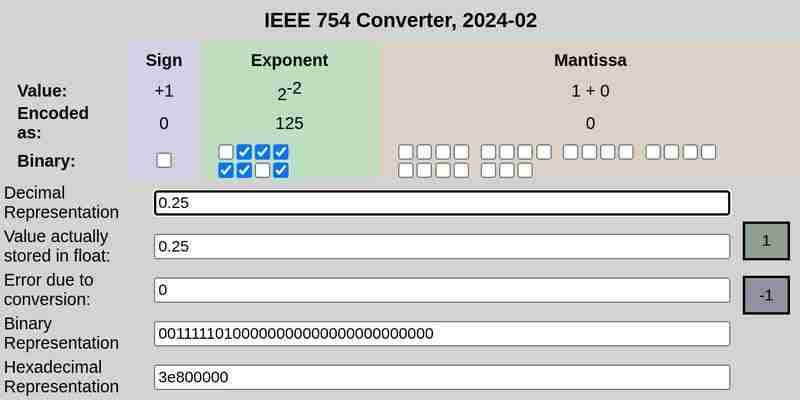
IEEE 754Notation von 0,1 bzw. 0,2:
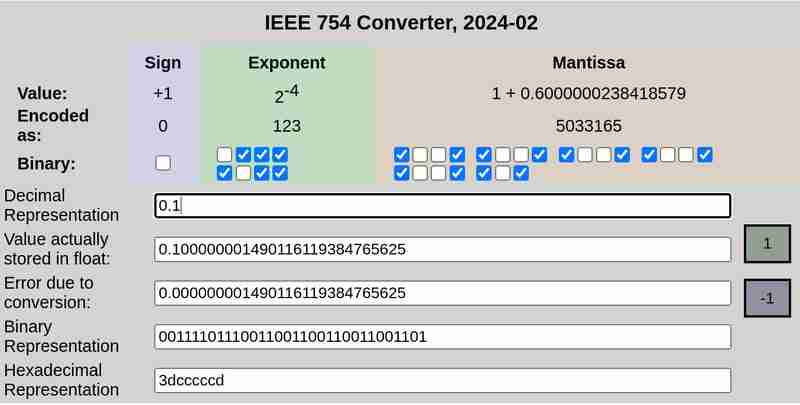
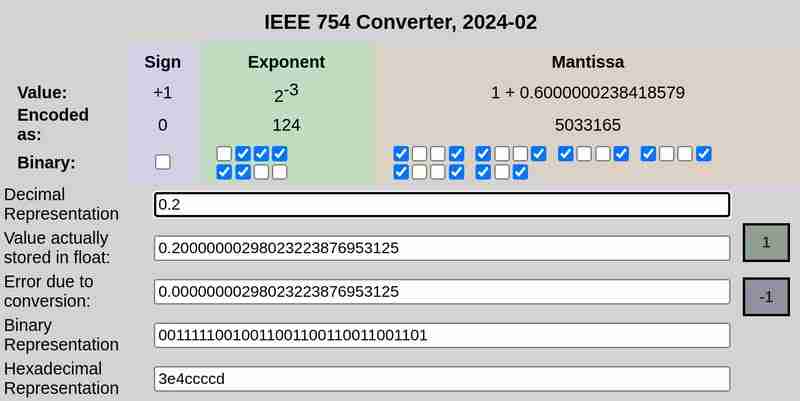
Bitte beachten Sie, dass der Fehler aufgrund der Konvertierung im Fall von 0,25 0 war, während 0,1 und 0,2 Fehler ungleich Null aufwiesen.
IEEE 754 definiert die folgenden Formate für die Darstellung von Gleitkommazahlen:
Einfache Genauigkeit (32 Bit): 1 Bit für Vorzeichen, 8 Bit für Exponent, 23 Bit für Mantisse
Doppelte Genauigkeit (64-Bit): 1 Bit für Vorzeichen, 11 Bit für Exponent, 52 Bit für Mantisse
Der Einfachheit halber betrachten wir das Format mit einfacher Genauigkeit, das 32 Bit verwendet.
Die 32-Bit-Darstellung von 0,1 ist:
0 01111011 10011001100110011001101
Here the first bit represents the sign (0 which means positive in this case), the next 8 bits (01111011) represent the exponent and the final 23 bits (10011001100110011001101) represent the mantissa.
This is not an exact representation. It represents ≈ 0.100000001490116119384765625
Similarly, the 32 bit representation of 0.2 is:
0 01111100 10011001100110011001101
This is not an exact representation either. It represents ≈ 0.20000000298023223876953125
When added, this results in:
0 01111101 11001101010011001100110
which is ≈ 0.30000001192092896 in decimal representation.
In conclusion, the seemingly perplexing result of 0.1 + 0.2 not yielding 0.3 is not an anomaly specific to JavaScript, but a consequence of the limitations of floating-point arithmetic across programming languages. The roots of this behaviour lie in the binary representation of numbers, which inherently leads to precision errors when handling certain fractions.
Das obige ist der detaillierte Inhalt vonJenseits von JavaScript – Warum es in der Programmierung nicht gleich ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

